Ordre de grandeur d'une énergie pour une rotation

[yy527]

Bonjour

Je souhaite savoir (sans forcément faire les calculs car le résultat est peut être évident pour vous) si la somme des travaux lors de la rotation du bras noir sur un quart de tour est positif ou négatif ?



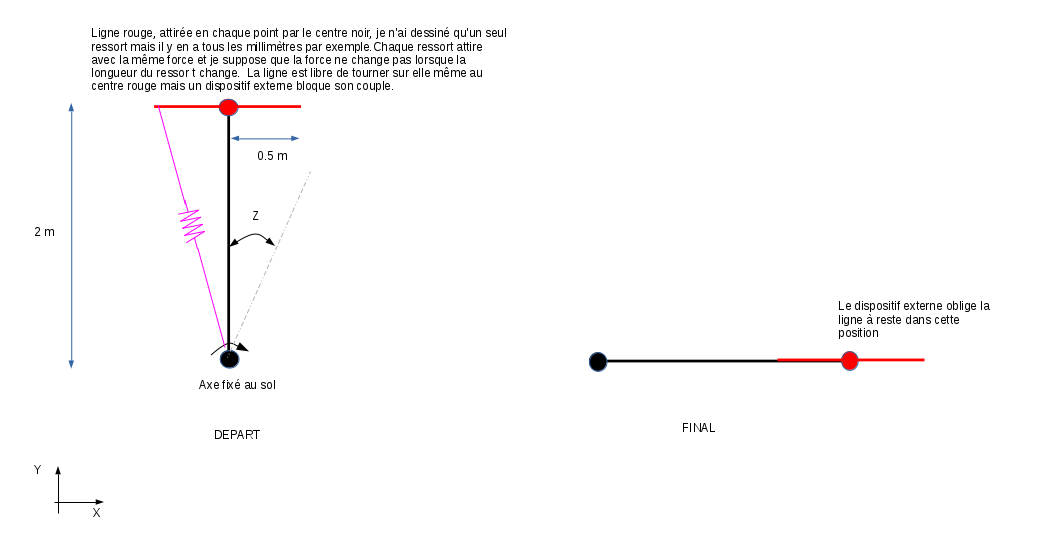
J'ai simplifié l'étude par une ligne mais au départ j'avais bien un volume pour avoir une inertie. Je considère que l'inertie de la ligne rouge est très importante pour qu'elle garde son orientation. Avant le départ, la ligne rouge est en translation vers la droite. Au départ, le bras noir la prend pour mettre son centre de gravité en rotation. J'ai dessiné la position finale. J'ai indiqué des dimensions pour avoir un ordre de grandeur.

Peut être qu'il est nécessaire de faire les calculs, dites moi. J'avais l'impression que la rotation fournissait un travail au bras noir mais ce n'est peut être pas aussi évident que cela.

Merci par avance

a++
-----

[Dynamix]

Salut
Si tes forces convergent vers le point noir , leur moment est nul en ce point .
Il n' y a aucune raison pour que la ligne noire tourne .

[yy527]

Avant le départ, la ligne rouge bouge en translation, elle a une vitesse, et son inertie fait qu'elle veut continuer mais juste à l'instant du départ j'attache le centre de gravité de la ligne rouge au bras noir et j'active les ressorts.

Merci

[Dynamix]

Je considère que l'inertie de la ligne rouge est très importante pour qu'elle garde son orientation.

Plus que très importante :
Carrément infinie .
Donc problème impossible .

j'active les ressorts.

Vu qu' il ne servent à rien je n' en vois pas l' intérêt .

[A voir en vidéo sur Futura]

[yy527]

ok, super, merci

[yy527]

Bonjour

Je modifie donc juste un peu le problème. Je considère qu'un dispositif externe oblige la barre rouge à rester dans son orientation.

J'ai fait des calculs pour les longueurs de ressorts cela donne :

Au départ la somme des longueurs des ressorts vaut:






Cela donne 2.02064 m

Précision de 1e-14

Au final la somme des longueurs des ressorts vaut:

2 m

Précision de 1e-14

Pour le travail de la somme des moments j'ai été obligé de faire le calcul avec une intégrale triple:

Moment sur l'axe x:



Moment sur l'axe y:



Energie perdue:

avec une précision de 2e-14

Energie gagnée:

avec une précision de 2e-14

J'ai fait les calculs avec python et Wolfram et je trouve le même résultat.

Est ce que cela est correct ?

a++

[Chanur]

Je considère qu'un dispositif externe oblige la barre rouge à rester dans son orientation.

Alors il faut aussi prendre en compte le travail fourni par ce "dispositif externe".

[Dynamix]

Au départ la somme des longueurs des ressorts vaut:

C' est du grand Nawack !
Si tu sommes des longueurs, le résultat est une longueur .
Des mètres plus des mètre , ça donne des mètres .
Les résultat de ton intégrale , c' est des mètres carrés donc une aire .
Que représente cette aire ???

[yy527]

Chanur: oui, tout à fait mais après je me suis dit que la barre rouge se déplace en translation et que le couple qu'elle reçoit ne peut pas changer l'énergie, qu'en pensez vous ?

Dynamix: l'intégrale n'est pas une aire, c'est la somme des longueurs des ressorts, oui ce sont des mètres et chaque ressort attire avec une force de 1N mais par rapport à sa longueur, en fait c'est une longueur de point, ouf tu vas pas aimer mais je pense que l'intégrale s'y retrouve bien, je pourrai faire les calculs plus réalistes en 3D mais cela va augmenter les intégrales et donc la possibilité d'une erreur de précision.

Il y a une petite erreur et ce n'est pas une erreur de précision car j'ai intégré en python avec 30 décimales.

Merci

[Dynamix]

l'intégrale n'est pas une aire

F1 a bien la dimension longueur ? (Y pour oui , N pour non)
∫L.dL a quelle dimension pour toi (dans ton monde) ?
Pour moi , dans mon monde , c' est L²

longueur de point, ouf tu vas pas aimer

Si , si .
J' adore !
Je le met en bonne place dans mon musée des grosses (très grosses) inepties .

Moment sur l'axe x:

Pour décrire un moment de forces , il faut préciser :
_L' ensemble de forces considéré
_Sur quel objet il s' applique
_En quel point on le considère
De plus il n' y a pas d' axe x sur ton dessin .

Au passage :
Avec tes barres noires , tes points rouges , tes boules bleues ...
On a plus l' impression de faire joujou avec des crayons de couleurs que de faire de la physique .

[Chanur]

Chanur: oui, tout à fait mais après je me suis dit que la barre rouge se déplace en translation et que le couple qu'elle reçoit ne peut pas changer l'énergie, qu'en pensez vous ?

Que je ne comprends pas du tout ce signifie "un couple peut (ou pas) changer d'énergie".
Le fait est que l'effort qui empêche la rotation de la barre rouge travaille (parce que le déplacement n'est pas orthogonal aux forces) et que tu ne tiens pas compte de ce travail.

Dynamix: l'intégrale n'est pas une aire, c'est la somme des longueurs des ressorts, oui ce sont des mètres et chaque ressort attire avec une force de 1N mais par rapport à sa longueur, en fait c'est une longueur de point, ouf tu vas pas aimer mais je pense que l'intégrale s'y retrouve bien, je pourrai faire les calculs plus réalistes en 3D mais cela va augmenter les intégrales et donc la possibilité d'une erreur de précision.

Tu lis ce que tu écris ? On n'augmente pas la précision d'un problème plan en le traitant en 3D, d'où tu sort ça ?


Par ailleurs si tu veux des réponses essaie au moins de poser correctement le problème. Par exemple :

Moment sur l'axe y:

C'est quoi y, un axe ? (quel axe ?) un angle ? (quel angle ?) Les deux au choix du lecteur ?

[yy527]

"Que je ne comprends pas du tout ce signifie "un couple peut (ou pas) changer d'énergie". la ligne rouge va recevoir un couple, et c'est bien un couple parce que les ressorts vont appliquer des moments mais l'axe au centre de la ligne rouge va réagir, ce que je veux dire c'est qu'appliquer un couple à un objet en translation ne diminue ou n'augmente pas son énergie cinétique ou potentielle.

"Tu lis ce que tu écris ? On n'augmente pas la précision d'un problème plan en le traitant en 3D, d'où tu sort ça ?" comme je fais des calculs numériques plus il y a d'intégrales et plus il y aura des imprécisions, avec un problème le plus simple possible cela limitera les imprécisions possibles des calculs numériques.

"C'est quoi y, un axe ? (quel axe ?) un angle ? (quel angle ?) Les deux au choix du lecteur ? " Effectivement, il y 2 axes, un est fixe au sol (le noir) et l'autre permet à la ligne rouge de tourner sur elle même, je calcule la sommes des forces en X et en Y au centre de la ligne rouge et je calcule l'énergie en faisant intégrale( force * angle). Voilà le dessin à jour:



Pour les intégrales je me suis gourré, il me faut que des intégrales doubles:





Et j'intègre x de 0 à 1 et z de 0 à pi/2, z est un angle et x une distance. Mais y'a encore une erreur.

Merci

a++

[Dynamix]

c'est bien un couple parce que...bla bla bla

Il n' y a que deux moyens de justifier un couple (et qui se déduisent l' un de l'autre) .
_La résultante est nulle .
_Le moment est identique en tout point .
Le reste , c' est du bla bla .

[Chanur]

"Que je ne comprends pas du tout ce signifie "un couple peut (ou pas) changer d'énergie". la ligne rouge va recevoir un couple, et c'est bien un couple parce que les ressorts vont appliquer des moments mais l'axe au centre de la ligne rouge va réagir, ce que je veux dire c'est qu'appliquer un couple à un objet en translation ne diminue ou n'augmente pas son énergie cinétique ou potentielle.

Je ne parle pas des ressorts mais du fait que la ligne rouge est guidée pour rester horizontale. Tu ne tiens pas compte du travail fourni par le guide.

[Dynamix]

Moment sur l'axe x:
Moment sur l'axe y:

Encore du nawack ...
Toutes les forces et les bras de leviers étant dans le plan XY , les moments sont tous perpendiculaires à ce plan sui vant la formule :
X Λ Y = Z

[yy527]

J'ai trouvé mon erreur, les 2 intégrales précédentes sont correctes. C'est la somme des ressorts qui était mauvaise car j'ai oublié de diviser par l'angle. Je trouve bien une différence d'énergie de 0.02064 J, ce que perdent les ressorts est gagné par le la rotation du bras noir.

a++