Utilisation du PFD

[tchoupieeee]

Bonjour,

Je viens encore à vous pour m'aider un résoudre une question sur un exercice de mécanique :

"


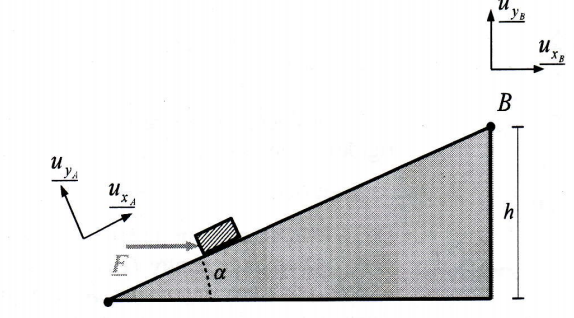
On considère une rampe (support rigide), d'angle a
avec le sol. h représente la hauteur de B par rapport
au sol. L'accélération de la pesanteur g est verticale
et orientée vers le bas.
Soit un mobile de masse m. considéré comme
ponctuel (point M), placé initialement sur la rampe
au point A. On exerce sur le mobile une force F
orientée horizontalement, dès I'instant initial et
pendant toute la durée de I'expérience.

Entre I et B, le glissement se fait avec un frottement solide de coefficient f On considère que le mobile
va glisser, et donc T = fN n'y a pas de frottement fluide. On prend A comme origine et on travaille sur
la base Uxa,Uya
1)Quelles sont les forces qui agissent sur le mobile ? Exprimer ces forces sur la base de travail.
2)Utiliser le principe fondamental pour déterminer le vecteur vitesse vB du mobile à
son passage en B , en fonction de h et a.
"
1) Je trouve 4 forces :
Poids = -mgsin(a) Uxa - mgcos(a) Uya
force F = Fcos(a)Uxa - F sin(a) Uya
réaction normal au support N = NUya
la réaction tangentielle au support T = - fNUxa ( car le mobile bouge )

2) Avec le PFD je ne vois pas comment faire, faut t-il trouver l’équation du mouvement ?? intégrer 2 fois l’équation trouvée avec le PFD ?
Sinon j'ai essayé de le faire avec le théorème de l’énergie cinétique :

je trouve que Vb = sqrt( (2h(-mgsin(a) +Fcos(a)-fN))/ msin(a) )

merci de m'indiquer la méthode avec le PFD ( principe fondamental de la dynamique)

Je vous souhaite une bonne soirée
-----

[sender]

Salut, tu as donc juste à appliquer le PFD avec les forces que tu as trouvé et projeter cela sur les deux axes x et y :
et tu projettes :



Du coup, tu as deux équations différentielles simples à résoudre :

[tchoupieeee]

oui je suis d'accord j'ai fais comme ça

en gros il n'y a pas d’accélération en Uya donc ici elle vaut 0

on considère que la première équation. Mais je ne vois pas ce qu'il faut trouver à la fin ? résoudre l'équation différentielle ? on trouvera x = .... et non la vitesse Vb
Pourriez vous décrire succinctement comment vous feriez s'il vous plait ?

[sender]

A priori, avec les équations différentielles écrites précédemment et les conditions initiales, tu peux répondre à toutes les question possible de ce pb. C'est la beauté de la mécanique :
pour revenir sur la question de la vitesse : il s'agit de la dérivée de la variable x(t) au point B : cela veut dire qu'il faut que tu arrive à écrire cette dérivée v(t) en fonction de la position x -> pour cela, en déterminant x(t)b, tu auras une relation entre x et t. Tu auras également déterminer v(t). Grâce à la relation précédente, tu changes ton t en x et tu auras donc une relation entre et v et x (v(x) = ...) ce qui te permettra de déterminer la solution.
Pour compléter : xb = h/sin(alpha).

Et je ne sais pas si tu en a besoin, mais la deuxième équation différentielle, compte tenu que la masse ne décolle pas (y=0), te permet de déterminer N en fonction de m,g,cos(alpha)

[A voir en vidéo sur Futura]

[tchoupieeee]

Excusez moi mais en esseyant de comprendre j'arrive avec mon x(t) = 1/2 *( -gsin(alpha) + ( F cos(alpha) -fN)/m)*t²
si je suis votre raisonnement : on sait que xb = h/sin(alpha) donc
h/sin(alpha) = 1/2 *( -gsin(alpha) + ( F cos(alpha) -fN)/m)*t²
puis on isole t ?
et ensuite on remplace ce t dans l'equation d(x)/dt soit v(t) ?

[Dynamix]

Salut

résoudre l'équation différentielle ? on trouvera x = .... et non la vitesse Vb

En intégrant une fois l' accélération , tu trouves la vitesse .