Calcul de longueur d'ondes - Modèle atomique de Bohr

[mohamed02]

Bonsoir !

J'étais en train de m'exercer sur le modèle atomique de Bohr ainsi que la formule de Balmer qui permet de calculer la longueur d'onde d'un photon émis à partir d'une transition de niveaux quantiques lorsque j'ai rencontré de grosses incohérences dans mes résultats...

Sans plus attendre, voici l'énoncé :

On considère un électron de l'atome d'hydrogène excité au niveau quantique n=5, combien de raies différentes peuvent-être émises lors du retour à l'état fondamental. Calculer dans chaque cas la fréquence et la longueur d'onde du photon émis.

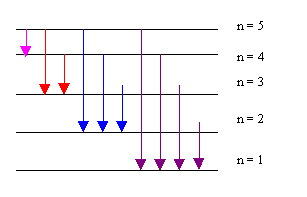
Tout d'abord, j'ai trouvé qu'il était possible de former dix raies différentes comme le corrigé l'indique :

L'électron peut passer de n=5 à n=1 ou alors il peut suivre des chemins intermédiaires comme n=5 puis n=3 puis n=1
L'inventaire de ces chemins intermédiaires indiquent 10 raies possibles.

Le problème est que lorsque j'essaye de calculer ne serait-ce qu'une longueur d'onde d'un photon émis, je ne sais pas où est-ce que je me trompe... Voici mon raisonnement :

On travaille dans l'atome d'hydrogène et on cherche à calculer une longueur d'onde, on peut donc se fier au modèle atomique de Bohr qui stipule que l'énergie d'un électron ne peut prendre que des valeurs discontinues (quanta). On peut donc travailler avec la formule suivante :


Or là nous cherchons l'énergie de transition du niveau excité à un niveau noté ce qui nous donne, par analogie :


Avec qui est l'énergie de Rydberg et qui vaut -13,6 eV

Cependant, lorsque que j'applique numériquement avec mes données, je trouve une longueur d'onde plus que douteuse, voici mon application numérique :


Je trouve donc que

Par la suite, j'utilise la formule de Planck-Einstein qui nous dit que : avec h la constante de Planck et nu la fréquence en s^-1

Je trouve une fréquence de (ce qui est déjà infiniment bas)

Enfin, à partir de la relation je trouve que la longueur d'onde du photon émis est de :

Je suis dans le flou, pouvez-vous m'éclaircir ? Merci beaucoup

Je me demandais aussi que pour trouver on pouvait tout simplement faire la différence et suivre le même raisonnement (est-ce possible?)
-----

[XK150]

Bonjour ,
Votre problème est traité en détail ici , par exemple :
http://physique.chimie.pagesperso-or...ESOLU_21_A.htm

[mach3]

1) Vous utilisez la valeur de h en J.s alors que vos énergies sont en eV. Il va falloir convertir qqchose.
2) Pour calculer la fréquence à partir de E=hv, il faut diviser l'énergie par h, pas la multiplier.

Avant de vous attaquer a la suite je vous suggère de bien reviser les bases (mathématiques de base genre ab=c <=> a=b/c et conversion des unités)

m@ch3