Mouvement Circulaire Uniforme Relativiste : Einstein s'est trompé ?

[Zefram Cochrane]

J'ouvre cette discussion pour ne pas poluer l'autre et elle mérite son petit sujet à elle.

dans le paragraphe 3 de l'article The Foundation of the Général Théorie of Relativity, Einstein nous dit que : "Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' ".

Je soutiens que cette affirmation est fausse par ce qu'elle ne tiens pas compte du phénomène d'aberration relativiste.
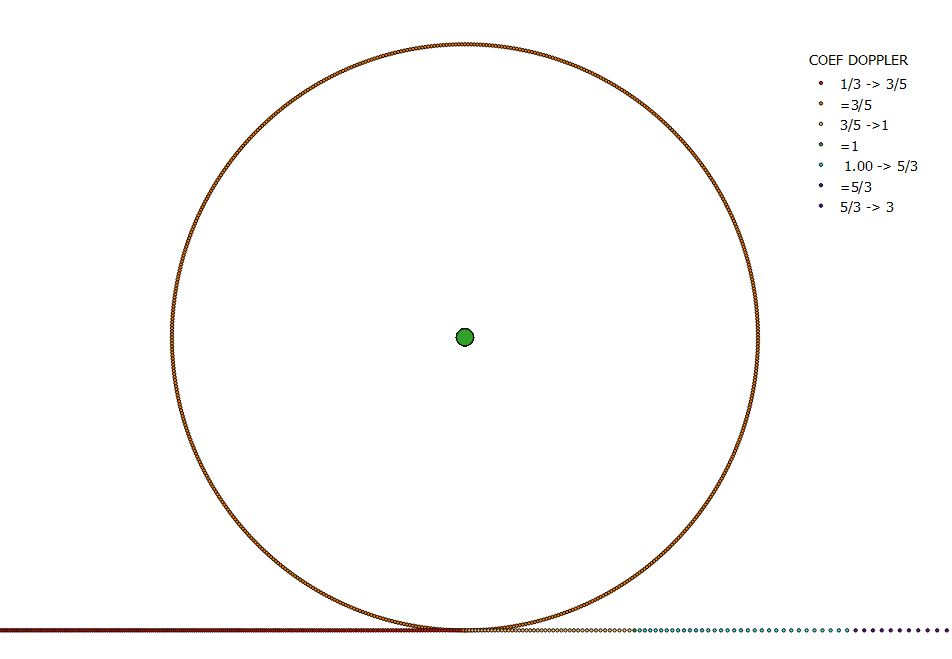
Si un observateur Voyageur arrive en MRU à V=0.8c sur l'entrée d'un circuit-looping constitué d'une boucle circulaire se lon un observateur Stationnaire de 36s.l de rayon. Du point de vue du Voyageur la boucle ne sera pas circulaire mais déformée par l'effet d'aberration de la lumière et par l'effet Doppler relativiste. Et, ce point de vue sera le même quand il en sort.

La question à se poser est quelle sera son point de vue lorsqu'il abordera la boucle, c'est-à-dire lorsque commençant sa rotation autour du centre du circuit looping et qu'il ressentira une accélération propre?
La réponse est que son point de vue sera identique lorsqu'il abordera la boucle que l'orsqu'il y entrera ou en sortira. La vision d'un observateur du paysage ne dépendant que de la vitesse ( au sens vecteur vitesse) relative de l'observateur par rapport au paysage.

Pour établir le schéma suivant: J'ai considéré 4 anneaux concentriques de rayon 6 ; 18 ; 30 et 36s.l

J'ai établi le tableau suivant :
Colonne A : O = 1 à 360.
Colonne B : o = O* 3.14 15 926 53 59
Colonne C : R = 6s.l ;18s.l ; 30s.l; 36s;l
Colonne D : Rx = R*COS(o)
Colonne E : Ry = R*SIN(o)
Colonne F : Xp = Rx
Colonne G : Yp = 36 + Ry
Ici je place Stationnaire à la base du circuit-looping au niveau de l'entrée et de la sortie de la boucle.

Colonne H : Tp = - RACINE( Xp^2 + Yp^2)
Si l'horloge de Stationnaire indique H=0s, alors uen horloge placé au point P de la boucle de rayon R indiquera H = Tp (Tp étant négatif).

On passe aux TLs pour connaitre la position de P par rapport au Voyageur de son point de vue.
Colonne I : Xp'= Xp*5/3 - Tp*4/3
Colonne J : Tp'= Tp*5/3 - Xp*4/3

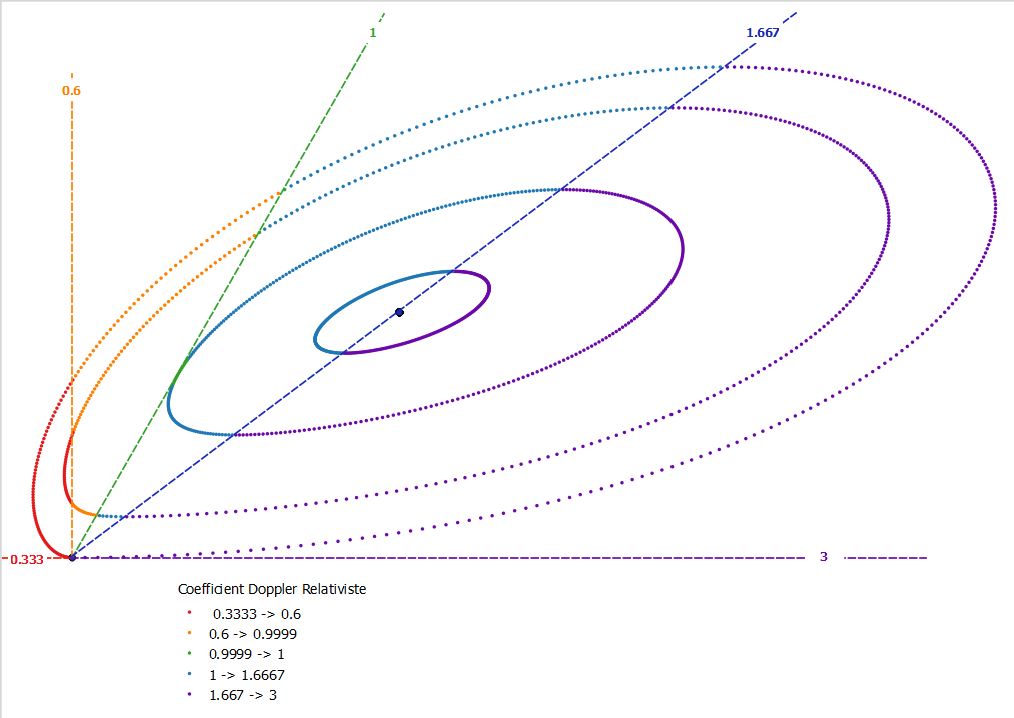
On a Yp' = Yp et je peux déjà en paramétrant tracer le contour des boucles du point de vue du Voyageur lorsqu'il se trouve à l'entrée de la boucle R36:


Le coefficient Doppler d'une horloge indique la vitesse de marche apparente de l'horloge de Stationnaire du point de vue de Voyageur.
Colonne K : Kv = Tp'/Tp

Si je dispose des observateurs Stationnaires avec des horloges à la base des boucles Ho (Xo =0 ; Yo=36) ; H6 (X6 = 0 ;Y6 = 60); R18 etc...

Comment le Voyageur verra t'il les Stationnaires évoluer alors qu'il est engagé dans la boucle R36?
En Imaginant les Stationnaires en vis-à-vis de celui situé au centre Ho, il va les voir suivre les trajectoires ovoïdes tout en restant en vis-à-vis par rapport au Stationnaire central que le Voyageur voit tourner autour de lui-même et dont l'horloge affiche une vitesse de marche de 5/3 plus rapide que celle du Voyageur.

Pour les autres Stationnaires, la vitesse de marche de leur horloge varie mais si on fait la moyenne des coefficients doppler relativistes, on trouve que sur un tour complêt, leur vitesse de marche est 5/3 fois plus rapide que celle du Voyageur.

Cette description du mouvement circulaire uniforme (relativiste) est peut-être sommaire, mais devrait logiquement, anéantir celle proposé par Einstein.

Cordialement,
Zefram
-----

[invite6c093f92]

"Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' ".

Je mets en gras...

En passant, un bon coup dans la charte...T'aurai pu titrer autrement... ...Bon, c'est les vacances mais quand même..

[Zefram Cochrane]

Salut Didier.
C'était peut-être clair dans l'esprit d'Einstein mais ce n'est pas ce que disent les calculs, qui sont justes.
Si Einstein avait raison, le Voyageur n'aurait pas la même vision de la Boucle R36 quand il s'engage dans la boucle et quand il est sur le point d'y entrer ou dans sortir.
Les questions à se poser :
Les raisons de symétrie invoquées par Einstein sont-elles justifiées pour décrire le MCU en relativité?
Pour moi la réponse est non et elles ne sont pas nécessaires non plus.
Si de ton coté tu penses que oui, merci de m'expliquer pourquoi par ce qu'en ce qui me concerne, ce n'est pas clair.

[Zefram Cochrane]

J'aurais du mettre en titre : Mouvement Circulaire Uniforme Relativiste : Einstein s'est-il trompé?

Si un modo peut corriger. SVP

[A voir en vidéo sur Futura]

[mach3]

"Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' "

pas encore fouillé (on verra si j'ai le temps), mais il se peut qu'il parle de "voir" au sens de reconstruction dans un hyperplan euclidien donnée et non de "voir" au sens vu avec ses yeux (avec les yeux on ne voit pas l'hyperplan euclidien mais le cône de lumière). Cette nuance est d'une importance fondamentale quand on parle d'aberration.

m@ch3

[Deedee81]

Bonjour,

Je déplace en physique, c'est mieux placé ici.

[Amanuensis]

[Je prends comme référence la traduction en anglais, donnée par http://hermes.ffn.ub.es/luisnavarro/...ivity_1916.pdf

Mon opinion:

Je lis cette partie de l'article traitée dans ce fil comme une démonstration par l'absurde. Car cela commence, la phrase juste avant celle citée, par «We shall show that for ... K' the above définition of the physical meaning of lengths and times cannot be maintained.» Et plus loin, en conclusion intermédiaire, on lit «Hence Euclidian geometry does not apply to K' (...) So, too, we are unable to introduce a time corresponding to physical requirements in K'»

La mention du temps est importante, car la phrase citée dans le message #1 est incomplète, la référence indique «may at the same time considered as a circle in the X' Y' plane in K'». La mention «at the same time » est critique, puisque c'est là où réside la prémisse fausse, ce qui rend la phrase non seulement absurde mais sans sens, faute de sens de «at the same time».

L'article développe ensuite la question du temps, et la conclusion finale est claire:

«We therefore reach the result : in the general theory of relativity, space and time cannot be defined in such a way that differences of the spatial co-ordinates can be directly measured by the unit measuring rod, or differences in the time co-ordinate by a standard clock.»

L'exemple des coordonnées tournantes doit être lu entièrement en fonction du résultat négatif indiqué, comme une démo par l'absurde (partant de prémisses contenant en particulier l'expression «au même instant»), et non comme le traitement correct en RG du cas d'un référentiel tournant.

[azizovsky]

: "Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' ".


Zefram

Notre point de départ est une question physico-mathématique : quelle est l’image (dans K’) par la transformation de Lorentz (TL) d’un front d’onde sphérique (dans K, en translation uniforme par rapport à K’), autrement dit d’un front d’événements simultanés? La simultanéité étant relative, le front image est un front ellipsoïdal spatio-temporel. Les sphères einsteiniennes sont des «sphères de synchronisation » qui définissent préalablement la simultanéité dans les deux systèmes K et K’(annexe 1).

il y'a lien avec ton problème .(Introduction historique : front d’onde sphérique d’Einstein et ellipsoïdal de Poincaré....).
http://cds.cern.ch/record/921614/files/0601090.pdf

[Zefram Cochrane]

Bonjour,
Voici la partie que j'ai "traduite" :
THE FOUNDATION OF THE GENERAL THEORY OF RELATIVITY
§3. Le continuum espace-temps. Nécessité de la co-variance générale pour les équations décrivant les lois générales de la nature.



<< Dans un espace libre de champ de gravitation, nous introduisons un système galiléen de référence K(x,y,z,t), et aussi un système de coordonnées K' (x', y',z',t') en rotation uniforme relativement à K. Plaçons les origines des deux systèmes, de manière à ce que leurs axes Z coïncident en permanence. Nous devons maintenant montrer que pour une mesure espace-temps dans le système K' la définition du sens physique des longueurs et temps ne peut pas être maintenue. >>
Einstein parle de la partie ci-dessous :
<<En mécanique classique, comme dans la relativité restreinte ( théorie spéciale de la relativité dans le texte ), les coordonnées de l'espace et du temps on un sens physique directe. Pour dire qu'un point-événement a la coordonnée X1, x1 veut dire que la projection du point-événement sur l'axe X1, déterminé par une baguette rigide et en accord avec les règles de la géométrie euclidienne, est obtenue en mesurant à partir d'une baguette donnée ( l'unité de longueur) x1 fois depuis l'origine des coordonnées le long de l'axe X1. Pour dire qu'un point-événement à la coordonnée X4, x4=t veut dire qu'une horloge standard, fabriquée pour mesurer le temps avec une période de temps définie, et qui est stationnaire relativement au système de coordonnées et coïncide pratiquement dans l'espace avec le point-événement (*), aura mesuré x4=t périodes à l'occurrence de l'événement.>>
(*) Nous assumons la possibilité de vérifier «*la simultanéité*» pour les événements dans le voisinage immédiat, ou plus précisément, pour le voisinage de la coïncidence immédiate dans l'espace-temps, sans donner une définition de ce concept fondamental.


<< Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' . Nous supposons que la circonférence du diamètre de ce cercle a été mesuré par une unité de mesure infiniment petite comparée au rayon, et nous avons le quotient des deux résultats. Si l'expérience a été réalisée avec une baguette de mesure au repos relativement au système galiléen K, le quotient sera égal à Pi. Avec une baguette de mesure au repos relativement à K', le quotient sera plus grand que Pi.
Cela se comprend facilement si nous envisageons l'ensemble du processus de mesure depuis le système «*stationnaire*» K, et prenons en considération que la règle de mesure appliquée à la périphérie est soumise à la contraction de Lorentz, tandis que celle appliquée le long du rayon pas . En conséquence la géométrie euclidienne ne s'applique pas à K'. La notion de coordonnée définie au-dessus, qui présuppose la validité de la géométrie euclidienne, s'effondre ainsi en relation avec le système K'. Donc, également, nous ne sommes pas capables d'introduire un temps correspondant aux conditions physiques requises dans K', indiqué par des horloges au repos dans le système K'.
Pour nous convaincre nous même de cette impossibilité, nous devons juste imaginer deux horloges de constitution identique placées, l'une à l'origine des coordonnées, et l'autre sur la circonférence du cercle, et toutes deux envisagées du point de vue du système K. Un observateur à l’origine commune des coordonnées, capable d'observer l'horloge de la circonférence avec des moyens lumineux, verra ainsi son décalage avec l'horloge derrière lui. Comme il ne se dira pas que la vitesse de la lumière le long du chemin en question dépend explicitement du temps, il interprétera son observation comme démontrant que l'horloge à la circonférence bat «*réellement*» plus lentement que l'horloge située à l'origine. Donc, il devra être obligé de définir le temps de telle manière que la marche de l'horloge dépende de la position de l'horloge.
Nous obtenons ainsi ce résultat : dans la théorie de la relativité générale, l'espace et le temps ne peuvent pas être définis de telle manière que la différence des coordonnées spatiales peuvent être mesurées directement par des baguettes de mesures unitaires, ou que les décalages temporels par des horloges standards.>>


J'ai buté aussi sur l'interprétation à donner à "at the same time" que j'ai plutôt vu au sens de " en même temps, si ..."
J'ai mis en gras ce qui me paraît faux car découlant de la phrase cité dans mon premier message.

[azizovsky]

<< Pour des raisons de symétrie, il est clair qu'un cercle autour de l'origine sur le plan X,Y de K doit être vu comme un cercle dans le plan X' Y' de K' . Nous supposons que la circonférence du diamètre de ce cercle a été mesuré par une unité de mesure infiniment petite comparée au rayon, et nous avons le quotient des deux résultats. Si l'expérience a été réalisée avec une baguette de mesure au repos relativement au système galiléen K, le quotient sera égal à Pi. Avec une baguette de mesure au repos relativement à K', le quotient sera plus grand que Pi.
.

je crois que Einstein fait allusion au paradoxe d'Ehrenfest *:

C'est le paradoxe d'Ehrenfest*: dans un repère en rotation, le rapport entre la circonférence et le diamètre est différent de
. Si la géométrie était euclidienne dans R', le disque serait «*voilé*» ou «*déchiré*».

* : https://fr.wikipedia.org/wiki/Paradoxe_d%27Ehrenfest

[azizovsky]

En plus, une équation de type définit une hyperbole au sens euclidien et une circonférence au sens de la géométrie minkowskienne.(d'après ce qu'il a dit, il parle du deuxième sens:le rapport entre la circonférence et le diamètre est différent de )

[Zefram Cochrane]

je crois que Einstein fait allusion au paradoxe d'Ehrenfest *:



* : https://fr.wikipedia.org/wiki/Paradoxe_d%27Ehrenfest

Je ne sais pas si vous êtes d'accord avec ce que je vais dire, mais j'ai l'impression que nous en soyons réduis à essayer de "comprendre" ce qu'à voulu dire Einstein dans la fameuse phrase1 (parce que c'est Einstein qui l'a dites).

La desciption du mouvement circulaire uniforme donnée par Einstein dans ce paragraphe est celle qui est pour l'heure adoptée.

Ce paragraphe servant d'introduction au pragraphes suivant et à justifier la démarche d'Einstein, je pense qu'en dépit du fait que la description du mouvement circulaire uniforme soit potentiellement erronée, elle n'enlève rien à la validité de la RG si cette description du MCU n'impacte pas la démarche de pensée aboutissant à la RG.

[azizovsky]

je pense qu'en dépit du fait que la description du mouvement circulaire uniforme soit potentiellement erronée.

dans quel sens ? (formules générale (FG): je ne comprend rien en application numérique(AN) sans FG), j'ai délaissé ce domaine..., pour l'instant ce que je sais sur la rotation d'un référentiel se trouve dans les pages 330,331 et 332 (physique théorique: théorie de champs de L.Landau et E.Lifchitz :''ellipses''):

il importe de noter que l'on ne peut utiliser un référentiel tournant que jusqu'à des distances égale à . Il apparaît de * que, pour , laquantité devient négative, ce qui est inadmissible ....
comme dans tous autres champ stationnaire, les horloges ne peuvent être synchronisées de façon univoque en tous les point d'un corps tournant ....
*

[Mailou75]

http://cds.cern.ch/record/921614/files/0601090.pdf

J'aime beaucoup la "parenthèse cosmologique" (p30)!
Quelqu'un aurait des infos sur cette relativité cinématique sous-jacente à l’ellipse de Poincaré ? Ca m'a l'air tout a fait intéressant

[Zefram Cochrane]

dans quel sens ? (formules générale (FG): je ne comprend rien en application numérique(AN) sans FG), j'ai délaissé ce domaine..., pour l'instant ce que je sais sur la rotation d'un référentiel se trouve dans les pages 330,331 et 332 (physique théorique: théorie de champs de L.Landau et E.Lifchitz :''ellipses''):

Génial. Et si je te demandais de m'expliquer ces pages, qu'est-ce que cela donne?

[Zefram Cochrane]

Bonjour,

Voici un schéma représentant la situation suivante:
Soit une caspule sur un wagon en MRU à V sur une voie et passant la base d'un phare d'une hauteur H.
Du fait de la vitesse limitée de la lumière, la l'observateur dans la capsule ne voit le sommet du phare un certain temps après avoir passé la base du phare.
Lorsque c'st le cas la capsule accélère verticalement et se met en rotation autour du sommet du phare.
Voici le schéma pour des vitesses allant de 0.1c à 0.8c et incrémentées de 0.1c.

[azizovsky]

Désolé pour le retard..., pour aboutir à ton dessin, je crois que tu as utilisé les TLs, et d'autres effets de la RR ou...?, mais quelle formules ?

ps: je ne suis ni pour ni contre tes idées, mais je veux savoir ce que reflète tes 'représentations' de l'espace-temps.

Du fait de la vitesse limitée de la lumière, la l'observateur dans la capsule ne voit le sommet du phare un certain temps après avoir passé la base du phare.

??

[Zefram Cochrane]

Salut Azizovsky.
Désolé pour le temps d'attente de la réponse.
J'ai un petit pb à vous soumettre et je n'arrive pas à trouver de réponse satifaisante. :
Un train arrive en MRU à 0.8c à la base d'une boucle circulaire de 360s.l de circonférence. L'entrée et la sortiede la boucle coïncident avec la base d'un phare dont le sommet se trouve au centre de la boucle de hauteur Ro. (Premier schéma de ce fil.)

A la base se trouve le Chef de gare qui verra défiler une longueur Lo' de train de 600s.l pendant un tour complêt.
Je voudrais déterminer comment le conducteur du train et le chef de gare verront ces 600 s.l de train se répartir sur la boucle.
Tous les dT=0.75s, Le conducteur verra un wagon de longueur propre 1s.l s'engager dans la boucle.
à Tr=n*dT parès avoir vu s'engager l'a tête du train,
il verra le conducteur à une distance

Nous avons donc Te = Tr - So

Le problème est que j'iggnore comment déterminer Te qui est ce qu'indiquera l'horloge de la boucle au moment où le Chef de gare VERRA la tête de train passer à son niveau (de l'horloge).

Le problème parrait simple mais c'est pourtant une véritable purge.
merci de votre aide ( à tous).

Je ne sais pas si vous deviez aller à la plage mais comme il fait gris et moche, autant faire des maths.

[azizovsky]

Bonjour ZC, je crois qu'il y'a un problème dans cette donnée ;

Tous les dT=0.75s, Le conducteur verra un wagon de longueur propre 1s.l s'engager dans la boucle.
,

si on place un observateur dans chaque wagon (comme le conducteur..), quel astuce utilisent ils pour synchroniser leurs horloges? (où se trouve l'origine du repère du temps du référentiel tournant?)

[Zefram Cochrane]

Au niveau des horloges du train. Pas de problème.
Les horloges sont synchronisées avant que le train s'engage dans la boucle.
Si Ã* T=0s l'horloge du conducteur indique T'=0s. Alors a T=450s , l'horloge du conducteur du train affiche T'=270s et il croise l'arrière du train dont l'horloge affiche T'= 750s.

[Zefram Cochrane]

Une intuition en passant.dans le repère du chef de gare la boucle est circulaire et homogène et dans le repère du train lorsqu'il achève son tour, les passagers voient la boucle ovoïde et inhomogene.
Comme sur la figure 1 pour la plu s grande boucle.

J'imagine que dans le référentiel du train les passagers voient (à T=450s) les wagons se répartir de manière homogène sur une boucle ovoïde et le chef de gare voit les wagons du train repartis de manière inhomogene sur la boucle circulaire.

[Zefram Cochrane]

Pour détailler ma réponse à Azizovsky:
La longueur du train est de 600s.l.
à T=Ti'=0s le conducteur et le chef de gare voient l'horloge du contrôleur afficher Hj'=-600s.
À T=450s , Ti'=270s=450*3/5 , Tj'=750s=450*5/3.
Le conducteur et le chef de gare auront vu le contrôleur vieillir de 1350s=450*3.
Le conducteur verra l'arrière du train achever son tour à Ti'=270+450*3=1620.
Il verra l'horloge du chef de gare afficher H=900s et celle de l'arrière du train Hj'= 750+270= 1020s; et. 1620-1020=600s soit le temps mis par la lumière pour parcourir 600s.l.

[azizovsky]

Bonjour, j'ai essayé de formuler le problème, mais je n'ai pas avancé d'un iota, un dessin (simple) de la tour, du circuit fermé,...,si tu as le temps, pour être sur que je suis sur les rails , merci d'avance .(c'est un vrai casse tête)

[Zefram Cochrane]

Bonjour,
Désolé pour le temps d'attente, mais j'ai trouvé la solution.
Si O est le Chef de gare situé à la base d'un phare de hauteur R=57,57.296s.l et à la base d'un circuit looping de 360s.l de circonférence . Il voit la voie + le circuit comme suit :
VOIE_Chef_de_gare.JPG

Maintenant si un observateur situé dans une locomotive arrive par la gauche à V=0.8c, voici ce qu'il voit lorsqu'il arrive à la base du phare.
VOIE_Passager.JPG

Les formules à utiliser sont :


Sp et Sp' sont la distance séparant le point P dans les repère respectif du Chef de gare et du Passager.
avec

On voit que du point de vue du Passager le Chef de gare passe du violet avant de tourner en suivant l'ovoïde autour du sommet du phare S tout en étant de plus en plus redschifté.

[Zefram Cochrane]

Imaginons à présent un train de 1800s.l de longueur et plaçons le Passager O à 600s.l de la tête du train. Lorsqu'il arrivera au niveau du Chef de gare. Il verra le conducteur du train sur la voie principale à 600s.l du Chef de gare. Le second tiers engagé dans la boucle ovoïde et le contrôleur situé en queue de train à 600s.l du Chef de gare.

De son point de vue. Le Chef de gare verra le conduteur à 200s.l de distance sur la voie. les 600 wagons (de 1s.l de longueur) se répartir sur les 360s.l de circonférence de la boucle circulaire et le contrôleur à 1800s.l de distance.
Pour calculer comment les wagons se répartissaient dans la boucle circulaire:
J'ai calculé en fonction de l'instant d'emission Te = N*0.75s ( le Chef de gare voit défiler 1 wagon de 1s.l de longueur toutes les 0.75s)
la position de tête du train P1 à Te. De là , j'ai calculé S1, la distance séparant P du Chef de gare, puis l'instant de réception T1 = Te+S1
Seulement, à T1 ne se trouve plus en P1.
J'ai donc caculé la position de la tête de train à T1 ce qui me donne le point P2 séparé de S2 et P2verra le Chef de gare à l'instant
T2=Te+S2. Je fais T2-T1 qui est positif si T2>T1, négatif sinon.Je réitère l'opération grâce à copier-coller, j'ai pu déterminer la position de chaque wagon de 1s.l avec une incertitude sur la position inférieure à 300m.

Cela me donne le schéma suivant :
TRAIN_Chef_de_gare.JPG

Puis, je passe par les "TLs" et j'obtiens la vision du train dans le repère du passager quand il passe au niveau du Chef de gare:
TRAIN_Passager.JPG

Mon intuition qui me disait que le train devait se répartir uniformément sur l'ovoïde quand on se plaçait du point de vue du passager était finalement fausse.

[Zefram Cochrane]

Bonjour,
Quand on regarde le premier schéma du message 24 : http://forums.futura-sciences.com/ph...ml#post5959567
On se demande si accessoirement, on ne décrirait pas également la vision d'un observateur au niveau du sol stationnaire par rapport à l'axe (S) d'une roue avançant horizontalement à V=0.8c vers la gauche.
C'est ce que j'ai voulu vérifier.

Soit un observateur (Vert) situé sur l'axe d'une roue de 600s.l de circonférence avançant horizontalement de gauche à droite sur une route à V=0.8c.
Voici ce que voit Vert :
sans la formule précise du petit problème que j'ai évoqué, il m'est difficile de représenter la vision de Vert des rayons de la roue, mais pour ce qui est du "pneu" il n'y a pas de soucis et n voit bien qu'au niveau du point de contact entre la roue et la route, le coefficient Doppler relativiste est 3/5.

Le paradoxe d'Ehrenfest cité par Azizofsky ( https://fr.wikipedia.org/wiki/Paradoxe_d%27Ehrenfest ) a pour origine le fait que pour un rayon en accélération comme un observateur situé sur la roue, la longueur apparente qui est une longueur coordonnée ,ici le rayon de la roue R', ne correspond pas à la longueur propre d'un règle , ici Ro du rayon de la roue mesurée par des graduations sur le rayon de la roue.
Le paradoxe d'Erenfest se présente un peu comme la version circulaire du paradoxe de la ficelle de Bell.

Si au repos. la roue mesure 600s.l de circonférence pour un rayon Ro=600/2Pi, à V=0.8c, Sa circonférence pour Vert devient 360 et sont rayon R=360/2Pi.

lorsque la vitesse tend vers c, on en déduit que le rayon tend vers 0.

Le schéma présenté dans ce message est ce qui se rapproche le plus de la description donnée par Einstein du mouvement circulaire uniforme à ceci près que la conformité ne concerne que Vert, que le rayon R est différent de Ro et que dans ma présentation, Pi ne varie pas.