Problème de Thomson

[geometrodynamics_of_QFT]

Bonjour,

Je souhaite avancer sur ce problème ouvert : trouver la position d'équilibre de N charges ponctuelles de charge q=1 à la surface d'une sphère S2 de rayon r=1.
On sait donc par la Loi de Coulomb, que l'énergie potentielle d'interaction électrostatique entre deux charges i et j est donnée par (où on a posé que la constante de coulomb k=1, et )

Le but est de minimiser le potentiel total avec N charges (c'est-à-dire annuler ses dérivées par rapport aux latitude et longitudes).
Ou alors, de maximiser la somme des distances, ce qui revient sans doute un peu au même.

On voit ici qu'une méthode basée sur une labellisation des coordonnées des différentes charges devient rapidement impraticable à mesure que N augmente.

Quelqu'un a-t-il des pistes? Que pensez-vous a priori de l'idée de trouver une solution purement géométrique sur une autre surface fermée sans bords, et ensuite de faire un mapping (et la labellisation en même temps) sur la sphère? De façon à s'affranchir, pour l'étape d'optimisation, de la géométrie sphérique et de sa trigonométrie ingérable?
-----

[LPFR]

Bonjour.
Il est évident que le problème n’a de solution unique que quand les charges sont situées aux sommets des polyèdres réguliers. Donc, pour un nombre de charges de 4, 6, 8, 20 et 12.

Pour tous les autres cas, les solutions sont probablement multiples (Continues ? Discrètes ?).
Au revoir.

[geometrodynamics_of_QFT]

Bonjour.
Il est évident que le problème n’a de solution unique que quand les charges sont situées aux sommets des polyèdres réguliers. Donc, pour un nombre de charges de 4, 6, 8, 20 et 12.

Pour tous les autres cas, les solutions sont probablement multiples (Continues ? Discrètes ?).
Au revoir.

On peut voir sur l'article wikipedia, qu'un polyèdre équivalent a été trouvé pour tous les nombres de charges jusque N=12 (donc pas uniquement 4,6,8 et 12, mais tous)
Même pour N=24 il a été trouvé à vrai dire : c'est un cube adouci.

Pour N=3, il s'agit d'une solution dans un plan : configuration en triangle..mais dégénérée donc pas unique, j'en conviens. Et il en est de même pour toutes les autres solutions....cela est dû à la symétrie sphérique : invariance par rotation autour du centre.

[LPFR]

Re.
D’accord. Au temps pour moi.
A+

[A voir en vidéo sur Futura]

[mach3]

Bonjour.
Il est évident que le problème n’a de solution unique que quand les charges sont situées aux sommets des polyèdres réguliers. Donc, pour un nombre de charges de 4, 6, 8, 20 et 12.

Pour tous les autres cas, les solutions sont probablement multiples (Continues ? Discrètes ?).
Au revoir.

attention, contrairement à ce que l'on pourrait croire, la solution pour 8 n'est pas le cube, mais l'antiprisme à base carré! Et il y en a un autre qui deconne comme ça, je ne sais plus si c'est 12 ou 20...

m@ch3

[phys4]

attention, contrairement à ce que l'on pourrait croire, la solution pour 8 n'est pas le cube, mais l'antiprisme à base carré! Et il y en a un autre qui deconne comme ça, je ne sais plus si c'est 12 ou 20...

m@ch3

Les solides à 6 et 8 faces sont complémentaires : cube et octaèdre s'obtiennent en remplaçant une face par un sommet et inversement,

il en est de même pour 12 et 20 : dodécaèdre et icosaèdre.

[mach3]

Pardon, mais je ne vois vraiment pas le rapport...

m@ch3

[phys4]

Comme signalé par LPFR, les polyèdres réguliers fournissent des arrangements de points dont l'équidistance est parfaite et qui sont donc des solutions stables évidentes du problème de Thomson, on retrouve d'ailleurs ces solutions dans le tableau de la référence donnée ci-dessous

[mach3]

Il est ecrit "Notably, the geometric solutions of the Thomson problem for N = 4, 6, and 12 electrons are known as Platonic solids whose faces are all congruent equilateral triangles. Numerical solutions for N = 8 and 20 are not the regular convex polyhedral configurations of the remaining two Platonic solids, whose faces are square and pentagonal, respectively."

m@ch3

[Amanuensis]

dont l'équidistance est parfaite et qui sont donc des solutions stables évidentes du problème de Thomson

Je voudrais voir une preuve de ces «donc» et «évidentes» ...

[geometrodynamics_of_QFT]

Je voudrais voir une preuve de ces «donc» et «évidentes» ...

Si les N points sont équidistants, et que vous avez besoin d'une autre preuve que cela pour réaliser qu'il s'agisse évidemment d'une solution (puisqu'une telle distribution minimise l'énergie potentielle, qui est précisément le problème à résoudre), alors c'est de la mauvaise volonté lol

Quant au caractère stable de la solution, là, je vous le concède, ça ne suffit pas...

[Amanuensis]

Si les N points sont équidistants, et que vous avez besoin d'une autre preuve que cela pour réaliser qu'il s'agisse évidemment d'une solution (puisqu'une telle distribution minimise l'énergie potentielle, qui est précisément le problème à résoudre), alors c'est de la mauvaise volonté lol

??? Je demande une preuve, pas une profession de foi associée à une agression.

La preuve à fournir est sur minimiser.

a) Les références réfutent l'idée que ce soit un minimum global ;

b) Reste éventuellement à montrer qu'il s'agit d'un minimum local ; or qu'une distance entre deux charges diminue n'implique pas que l'énergie potentielle totale augmente, quand elle s'accompagne d'une augmentation d'autres distances entre charges.

[geometrodynamics_of_QFT]

Où avez-vous vu une aggression?

a) Les références réfutent l'idée que ce soit un minimum global ;

Quelles références?
Sur l'article de wikipedia, on lit :
"Minimum energy configurations have been rigorously identified in only a handful of cases."

Bien sûr, une assertion sur Wikipedia ne constitue pas une preuve en soi (et n'a a priori aucune valeur), mais les différents cas cités (dont N=6 et N=12 dont parlait phys4) sont référencés par des articles payants.
Sauf pour le cas N=5, voici l'article en question, dont l'abstract stipule :
"We give a rigorous computer-assisted proof that the triangular bi-pyramid is the unique configuration of 5 points on the 2-sphere that globally minimizes the Coulomb (1/r) potential"

b) Reste éventuellement à montrer qu'il s'agit d'un minimum local ; or qu'une distance entre deux charges diminue n'implique pas que l'énergie potentielle totale augmente, quand elle s'accompagne d'une augmentation d'autres distances entre charges.

Je viens de penser à quelque chose du genre :
Comme l'énergie potentielle est en 1/r, sa dérivée est -1/r² (et n'est pas linéaire)

Donc lorsqu'on rapproche 2 charges, l'énergie potentielle associée à ces 2 charges augmente plus que l'énergie potentielle associée à 2 charges qu'on éloignerait de la même distance (car 1/(r-epsilon)² > 1/(r+espilon)²)
Donc une configuration où toutes les charges sont équidistantes est forcément un minimum global?

(j'espère que ça passera...c'est le genre de réponses que je mettais aux exams quand je ne savais pas trop )

Non sérieusement...Il doit bien y avoir moyen de montrer votre point b)...laissez-moi mijoter...

[Amanuensis]

Quelles références?

c'est de la mauvaise volonté lol

. . .

[geometrodynamics_of_QFT]

. . .

Les seules références dans cette discussion sont l'article de wikipedia, et je montre dans mon message qu'il dit l'inverse de ce que vous avanciez...
Du coup je ne comprends pas trop à quelle référence vous faites allusion.

[geometrodynamics_of_QFT]

Que pensez-vous a priori de l'idée de trouver une solution purement géométrique sur une autre surface fermée sans bords, et ensuite de faire un mapping (et la labellisation en même temps) sur la sphère? De façon à s'affranchir, pour l'étape d'optimisation, de la géométrie sphérique et de sa trigonométrie ingérable?

Par exemple, si on résout le problème sur un tore (donc un rectangle avec des conditions aux limites périodiques), est-il possible d'ensuite effectuer un changement de coordonnées pour passer d'une géométrie plane à une géométrie sphérique?
Un des côtés du rectangle deviendrait un grand méridien (on enroule ensuite le rectangle jusqu'à ce que le côté opposé revienne au méridien de départ) et les deux côtés adjacents deviendraient des pôles.

[geometrodynamics_of_QFT]

Dit autrement : Comment paramétrer la surface d'une sphère pour qu'elle corresponde à une surface doublement périodique? Afin de pouvoir faire une bijection de la surface de la sphère vers le tore (qui sont deux surfaces fermées sans bord)
Et donc de pouvoir résoudre le problème sur le tore, ce qui est sans doute pus facile.

[mach3]

La sphère et le tore n'etant pas topologiquement équivalents, ca me parait difficile...

m@ch3

[geometrodynamics_of_QFT]

Comme un petit dessin vaut souvent mieux qu'un long discours:


Est-il possible de trouver une bijection entre le carré périodique de côté 2pi et la surface sphérique?

Ils sont effectivement topologiquement différents, mais qu'est-ce qui empêche fondamentalement de trouver une correspondance 2 à 2 entre un point de la sphère et un point du carré?

style
x/2pi --> theta
y/2pi --> ~phi (moyennant détails techniques de régulation pour que l'image soit entre -pi/2 et pi/2)

[geometrodynamics_of_QFT]

Merci aux futurs intervenants qui désirent répondre sur l'aspect topologique (donc par rapport aux messages #16, #17, #18 et #19) de le faire dans le forum mathématique sur ce fil-ici, où une discussion spécialement dédiée à cette problématique a été ouverte.

[azizovsky]

Ils sont effectivement topologiquement différents, mais qu'est-ce qui empêche fondamentalement de trouver une correspondance 2 à 2 entre un point de la sphère et un point du carré?

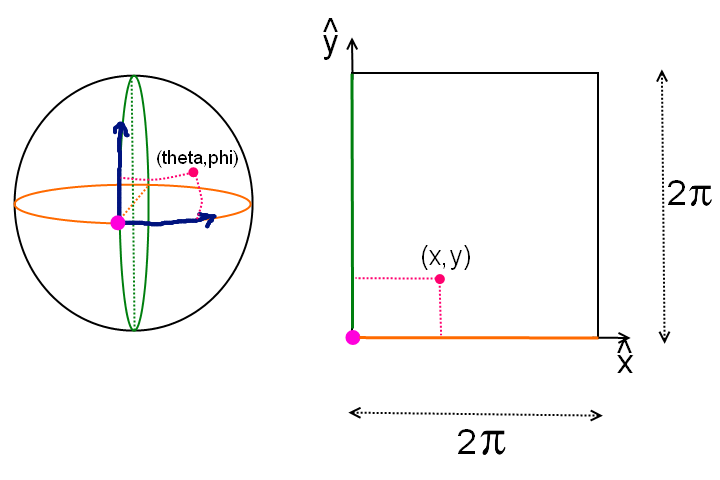
si, il y'en a , je vais essayer de me rappeler comment (je crois d= kr)

[azizovsky]

si, il y'en a , je vais essayer de me rappeler comment (je crois d= kr)

may, il suffit de remarquer que le cube est homéomorphe à la boule )

[geometrodynamics_of_QFT]

Oui mais je viens de voir qu'un homéomorphisme conservait la compacité...
Or, un cube I² (un carré plan donc?) est semi-compact, et la boule B² est compacte

Et puis, parle-t-on bien de surfaces et non de volumes? La boule c'est un volume non?
Et aussi, qu'est-ce que ? Aurais-tu une quelconque référence qui parle de cet homéomorphisme?
Merci

[geometrodynamics_of_QFT]

J'ai vu aussi sur l'article wikipedia de la boule, que suivant la norme utilisée, la boule était, dans R², un disque (norme euclidienne) ou un carré (norme "infini").
En fait, il est même dit que
"Dans l'espace réel à trois dimensions muni de la norme infini, les boules ont une forme cubique avec des faces perpendiculaires aux axes."

Mais tout cela reste anecdotique par rapport au problème, puisqu'il s'agit ici de trouver une bijection entre 2 surfaces, et non entre 2 volumes.

[azizovsky]

et pour est la longueur du vecteur colinéaire au vecteur et le point appartienne à la frontière du cube..., c'est tout ce qu'il y'a dans ma jarre , à toi de creuser la question .

[geometrodynamics_of_QFT]

Merci pour la piste

[azizovsky]

tu parle carrément d'un carré , https://fr.wikipedia.org/wiki/Bouteille_de_Klein.

ps: il y'a deux type de variété à 2 D, les M(g) (sphère à g ances) et M(u) (élimination de u disque D² disjoints deux à deux .....) et une troisième (panachée: on colle g ances et un bandes de Moebius....

[geometrodynamics_of_QFT]

La discussion (purement mathématique) se poursuit ici...

[azizovsky]

on ai en physique voir aussi https://fr.wikipedia.org/wiki/Tore

détail https://fr.wikipedia.org/wiki/Tore#/media/File:Tore.svg

[geometrodynamics_of_QFT]

Non mais merci, je sais bien ce qu'est un tore
J'en parle dans le message #16....

Et pareil pour la bouteille de Klein, j'ai vu toutes les vidéos de la géniale chaîne Numberphile

D'ailleurs pour ceux interessés par la bouteille de Klein:
https://www.youtube.com/watch?v=AAsICMPwGPY
https://www.youtube.com/watch?v=-k3mVnRlQLU
https://www.youtube.com/watch?v=I3ZlhxaT_Ko
https://www.youtube.com/watch?v=2g3sdzgSABM

Le truc ici c'est de trouver une surface plane dans R² qui se bijecte vers une sphère, et non un tore (car le problème de Thomson, c'est sur une sphère, pas un tore)

Mais t'as raison, on est en physique ici, donc pour continuer la discussion topologique, c'est dans le forum maths