Bonjour à tous !
Je suis bloqué sur un exercice (pour changer) et je ne sais pas ce que j'ai raté :
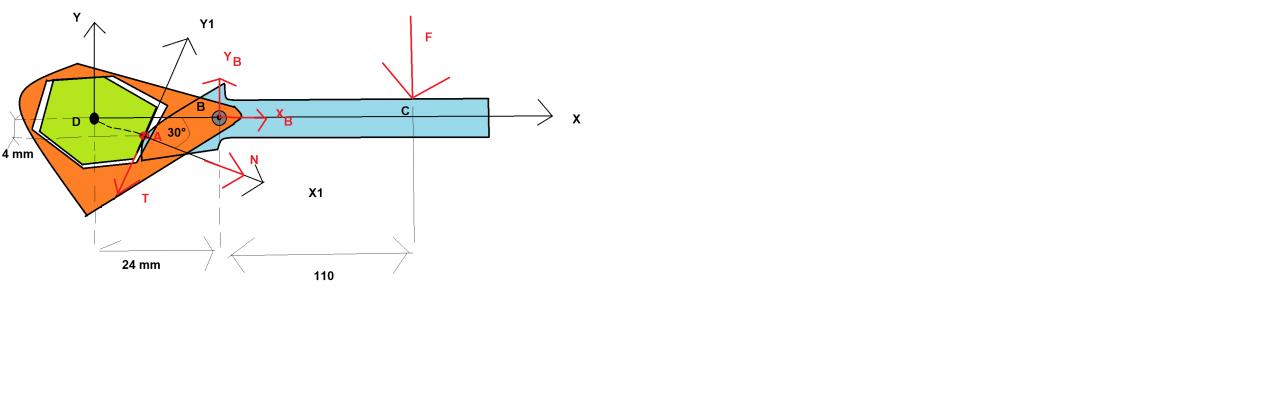
L'énoncé tiré du Fanchon : La clé à excentrique proposée permet de serrer des écrous ou des vis(3) de dimensions différentes. Le profils en came du manche (1) est réalisée de façon que la droite AD conserve une direction fixe (30°) par rapport au manche, quel que soit l'écrou.(10daN), perpendiculaire au manche, schématise l'action de l'opérateur ; les poids sont négligés; le frottement en A est égal
= 0,15.
1) Isoler le manche (1), en déduire les actions exercées en A et B.
** j'ai calculé les moments en mm**
Je fais ce que dit l'exercice, j'isole (1).
Je fais le bilan des actions mécaniques extérieures :
Je pose un repère en A (A,x1,y1,z1) associé aux forces de frottements N et T appliquées au point A .
En B, j'en déduis que c'est une pivot d'axe:

Nous avons l'action de l'opérateur qui est connue F = - 10 daN
Nous avons 4 inconnues : N, T, B_{x}, B_{Y} et 1 connue : F
Selon mon bilan , j'ai le choix d'appliquer le PFS au point A ou au point B. Je choisis de le faire au point B.
Je transporte l'ensemble des forces au point B :
<=>
Avant de calculer le moment de N et T au point B, je projette leurs vecteurs dans la base B(D,X,Y,Z) , ce qui nous donne :
Il nous manque la distance BD mais qui est implicitement donnée par l'angle et la hauteur. Donc, DA = 4 / sin(30) =8 .
La projection de DA sur le repère (0,X,Y,Z) est : cos(30) x - sin(30)y
Calcul de la force normal au point B :
<=>
Calcul de la force trangente au point B :
<=>
Ayant l'ensemble des moments des forces extérieurs transportés au point B, nous pouvons appliquer le PFS au point B:
(1) : Projection des résultantes sur l'axe des X :
(2) : Projection des résultantes sur l'axe des Y :
(3) : Projection des moments au point B sur l'axe des Z :
4 Inconnus pour 3 équations, le système semble être inrésolvable... Sauf qu'on est en frottement et on peut donc utiliser la loi de coulomb tels que :
(4) : T = f N avec f=0.15
(3) :
(3) :
N = 157.4 daN au lieu de 59.8 daN...
Franchement, je ne vois pas où je me suis planté.
Si quelqu'un peut m'aider, j'en serai grandement reconnaissant.
-----