Démarche : pour quelle fréquence, le courant i est-il nul ?

[Loosgin]

Madame, Monsieur,
j'ai fait cet exercice où l'on cherche la fréquence qui annule le courant i :
http://fabrice.sincere.pagesperso-or...ite%203-09.pdf
J'ai 2 questions, la première :

- Pourquoi est en quelque sorte "la figure de proue" de ce nombre complexe ?

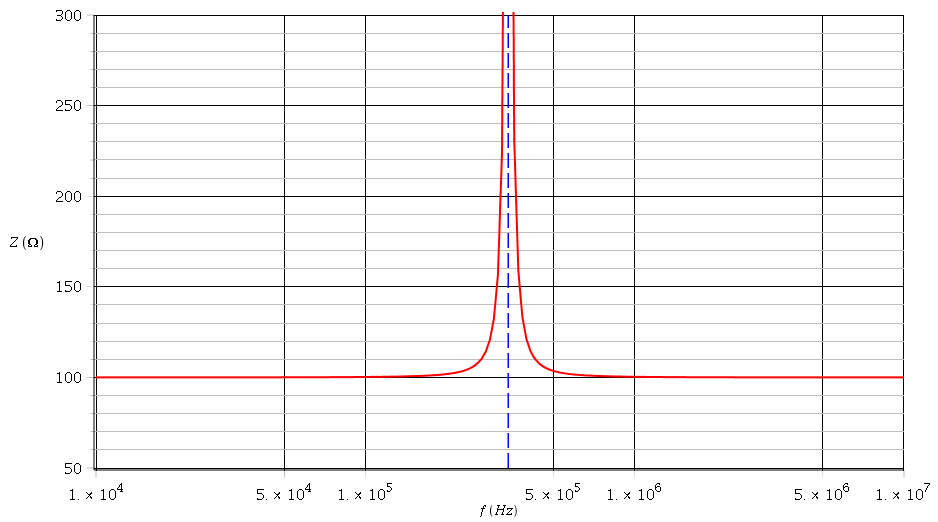
En effet, en calculant le module de l'impédance (long et fastidieux mais toujours moins qu'à la main) sur excel (avec f comme variable), je retombe bien sur la solution proposée par cet exercice.
module.PNG
Autrement dit, comment cela se fait que le résultat dépend du dénominateur (et en plus du dénominateur de l'impédance complexe qui plus est !) ?

-Deuxième question :
Est-ce une bonne démarche de partir sur les limites (en s'appuyant sur le module du l'impédance complexe évidemment) pour trouver la valeur de oméga ?
J'ai posé :



Si oui, pourquoi alors je trouve que le module de ce nombre complexe tend vers R² lorsque f tend vers l'infini ? alors que visiblement (montré numériquement) le module atteint sa plus haute valeur lorsque f est égal à 340 kHz.
Je vous remercie par avance pour toutes réponses.
-----

[f6bes]

Bjr à toi,
Tu nous montres un beau cicruit bouchon avec L et C.
Quelle est la caractéristique principale d'un circuit bouchon !!
Il se passe quoi si un courant alternatif de fréquence F se "heurte"
à un circuit LC de ce type.

Je te laisse calculer F connaissant L et C.
Bonne journée

[petitmousse49]

Bonjour

long et fastidieux mais toujours moins qu'à la main

Tu trouves vraiment long d'écrire que le module de A+jB est ?
Il me semble intéressant de réfléchir à la signification physique des résultats. Tu sais bien sûr que le module de l'impédance d'une bobine est Z_L=Lω alors que le module de l'impédance d'un condensateur est Z_C=1/(Cω)
A basse fréquence : Z_C>>Z_L : le courant traversant R traverse quasi intégralement L : tout se passe comme si le condensateur n'existait pas : Z peu différent de R+jLω on voit bien que la limite à basse fréquence de Z est R.
A haute fréquence : Z_C<<Z_L : le courant traversant R traverse quasi intégralement la branche de C : tout se passe comme si la bobine n'existait pas : Z peu différent de R+1/(jCω) on voit bien que la limite à haute fréquence de Z est R.
En revanche, comme déjà expliqué, le module de Z tend vers l'infini pour la fréquence propre du circuit. Voici la courbe représentant la variation du module de z en fonction de f en choisissant R=100Ω. Attention : l'échelle des fréquence est logarithmique. Avec les valeurs numériques de L et C fournies sur le site, le module de Z reste très proche de R sauf aux fréquences proches de la fréquence propre.

[Loosgin]

Tout d'abord, merci encore pour vos retours qui sont très instructifs. Grâce à vos retours, j'ai pu faire quelques recherches ciblées sur le net autour de ces notions inconnues pour moi (jusqu'à maintenant) : comme le circuit bouchon, la fréquence propre d'un circuit ou encore l'antirésonance(résonance pour un circuit parallèle).

Quelle est la caractéristique principale d'un circuit bouchon !!

La caractéristique principale d'un circuit bouchon est d'avoir une impédance infinie lorsque la fréquence f avoisine sa fréquence propre f0 ? C'est la définition même de l'antirésonance, enfin si je ne lis pas de travers.

Tu trouves vraiment long d'écrire que le module de A+jB est ?

Celui ça va mais transcrire le module de l'exo sur excel =SQRT((POWER($F$9,2))+((($F$7* $F$7)*POWER($F$8*A2,2))/(POWER((-1+($F$7*POWER($F$8*A2,2)*$F$6) ),2)))) ... C'est pénible !

A basse fréquence : ZC>>ZL : le courant traversant R traverse quasi intégralement L : tout se passe comme si le condensateur n'existait pas : Z peu différent de R+jLω on voit bien que la limite à basse fréquence de Z est R.

OK !

A haute fréquence : ZC<<ZL : le courant traversant R traverse quasi intégralement la branche de C : tout se passe comme si la bobine n'existait pas : Z peu différent de R+1/(jCω) on voit bien que la limite à haute fréquence de Z est R.

OK !
Donc si je comprends bien, en présence d'un circuit bouchon, il suffit d'appliquer la formule de Thomson pour retrouver la fréquence propre du circuit ? Sa formule est empirique où elle s'appuie sur un raisonnement ?

Le graphique que tu as attaché ci-joint, c'est un diagramme de bode ? l'échelle est semi-logarithmique ? Visiblement de logarithmique base 10 ? Comment tu fais pour passer de l'échelle logarithmique à linéaire ?

Merci encore.

[A voir en vidéo sur Futura]

[f6bes]

Remoi,
Tu dis :
"....La caractéristique principale d'un circuit bouchon est d'avoir une impédance infinie lorsque la fréquence f avoisine sa fréquence propre f0 ? C'est la définition même de l'antirésonance, enfin si je ne lis pas de travers...."

Je ne sais pas trop ce que peut vouloir dire : ..." impédance infinie lorsque la fréquence f avoisine
sa fréquence propre f0.." ?

Pour moi un circuit antirésonant ets un circuit ou L et C sont...en série ( et non pas en paralléle).
Dans ce cas ce ciruit serie laisse passer la fréquence de LC et atténue et bloque les fréquences
autres que F de L et C.
Ca laisse passer F à l'inverse de d'un circuit bouchon qui bloque lui; la F
Bonne soirée

[Loosgin]

Je ne sais pas trop ce que peut vouloir dire : ..." impédance infinie lorsque la fréquence f avoisine
sa fréquence propre f0.." ?

f est fréquence variable.
f0 est une constante dépendant des caractéristiques du circuit : L et C
J'ai manqué de rigueur dans mes propos : je voulais dire que le module de l'impédance complexe de ce circuit était infini lorsque la fréquence f avoisine sa fréquence propre appelée f0.

Pour moi un circuit antirésonant ets un circuit ou L et C sont...en série ( et non pas en paralléle).
Dans ce cas ce ciruit serie laisse passer la fréquence de LC et atténue et bloque les fréquences
autres que F de L et C.
Ca laisse passer F à l'inverse de d'un circuit bouchon qui bloque lui; la F

J'ai peut-être mal compris alors, en m'appuyant sur ce site : http://www.chimix.com/an10/sup10/min02.html

Qu’appelle-t-on résonance en intensité dans un circuit ?
Lorsque la fréquence w de l'excitateur ( la tension alternative de fem e(t) ) est égale à la fréquence propre w0 du résonateur ( le circuit RLC), la valeur efficace de l'intensité passe par une valeur d'autant plus importante que la résistance R est plus faible.
Par analogie que peut-on appeler antirésonance en intensité ?
L'impédance du dipôle est maximale et la valeur efficace de l'intensité est nulle.

[petitmousse49]

Puisque, en valeurs efficaces, I=U/Z, on voit bien que, pour une tension sinusoïdale de valeur efficace U donnée non nulle, l'intensité est nulle lorsque Z tend vers l'infini et il est facile de démontrer que Z tend vers l'infini quand f tend vers la fréquence propre (voir ton document) . Physiquement cela s'explique par le fait que la tension sinusoïdale crée dans la branche de L un courant , dans la branche de C un autre courant, les 'intensités instantanés de ces deux courants dérivés étant de même fréquence, de même amplitude mais en opposition de phase. Le courant principal qui en résulte a donc, selon la loi des nœuds, une intensité instantanée nulle à chaque instant.
Je n'ai pas tracé un diagramme de Bode. Le fait d'utiliser une échelle logarithmique pour les fréquences constitue une méthode simple et pratique de visualiser une variation de grandeur (Z ici) sur un très large intervalle de fréquences.

[Loosgin]

Puisque, en valeurs efficaces, I=U/Z, on voit bien que, pour une tension sinusoïdale de valeur efficace U donnée non nulle, l'intensité est nulle lorsque Z tend vers l'infini et il est facile de démontrer que Z tend vers l'infini quand f tend vers la fréquence propre (voir ton document) . Physiquement cela s'explique par le fait que la tension sinusoïdale crée dans la branche de L un courant , dans la branche de C un autre courant, les 'intensités instantanés de ces deux courants dérivés étant de même fréquence, de même amplitude mais en opposition de phase. Le courant principal qui en résulte a donc, selon la loi des nœuds, une intensité instantanée nulle à chaque instant.

ça le mérite d'être limpide ! i(t)=ic(t)-il(t) ou i(t) = il(t)-ic(t) avec V.A(ic(t)) = V.A(il(t)) et i(t), ic(t) et il(t) des fonctions de la forme I(c/l) sin(wt+ phi(c/l))

Je n'ai pas été assez clair dans mon précédent message, la formule de thomson, c'est-à-dire c'est de l'empirique ? Je présume que oui puisque je n'arrive pas à mettre la main sur une démo' .

Je n'ai pas tracé un diagramme de Bode. Le fait d'utiliser une échelle logarithmique pour les fréquences constitue une méthode simple et pratique de visualiser une variation de grandeur (Z ici) sur un très large intervalle de fréquences.

Merci pour ces infos. Et comment tu passes de l'échelle logarithmique au linéaire ? Je sais que log (10^4) en base 10 est égal à 4

[petitmousse49]

La formule que tu fournis concernant f_o correspond à LCω_o²=1 puisque ω_o=2πf_o... La démonstration a donc bien été faite...
Pour l'échelle logarithmique, tu porte les valeurs de f avec une abscisse proportionnelle à log(f) : l'écartement de 10⁴ à 10⁵
est ainsi le même sur le graphe qu'entre 10⁵ et 10⁶, puisque dans les deux cas, log(f) augmente de 1 unité...

[Loosgin]

Cette formule elle-même découle du dénominateur de l'impédance complexe du circuit, donc j'en conclus que la démo de cette formule se fait à l'aide de l'impedance équivalente complexe du circuit.

Merci pour vos retours et votre patience