Quadrupole en contact avec conducteur

[Martth]

Bonjour,

J'espère que cette question n'a pas été posé avant, j'ai quand même fait mes recherches evidemment.
Je suis tombé sur un problème d'electrodynamique qui, me pose un certain problème, le voici:
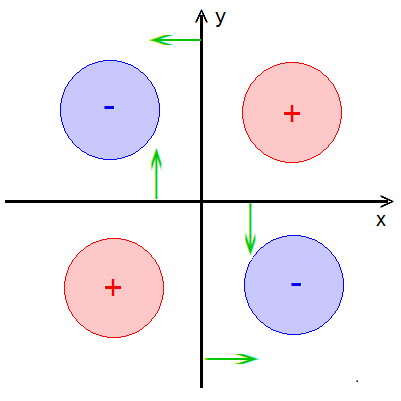
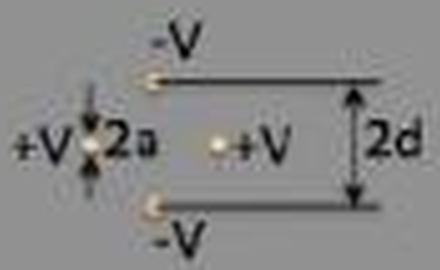
J'ai un quadrupole, i.e, 4 pointes auxquelles on applique un potentiel de -V pour deux d'entre eux et +V pour les deux autres. Ces pointes sont misent en contact avec une plaque conductrice et on me demande de trouver les surfaces equipotentielles.


En fait je me doute a quoi cela resemblera de part la symmetrie du systeme mais je en sais pas comment les retrouver mathématiquement. J'imagine que il me faudrait faire la superposition de chaque contribution des pointes. Normalement le champs electrique est égale au gradient du potentiel donc il devrais radier des pointes et je suppose que j'aurais une diminution en \frac{1}{r} (je sais plus comment faire des balise latex ici!).

Si quelqu'un peut m'éclairer ca serait bien apprécié!


Merci
-----

[penthode]

on ne parle pas le même français de l'autre coté de la mare aux harengs...

je te suggère de nous faire un scan du sujet in extenso , avec ses figures .

[Opabinia]

Bonjour,

Il manque quelques précisions:
a) le quadrupôle est-il bien constitué de 4 pointes dont les potentiels (±V) alternant aux sommets d'un carré ?
b) n'envisage-t-on pas des distances très grandes par rapport à l'arête de ce dernier ?

La forme des lignes de courant présentera probablement les même éléments de symétrie que le carré: 8 axes de symétrie, portant les médianes ou les diagonales.

Tu auras sans doute intérêt à centrer le carré sur l'origine; placer les 4 sommets sur les axes ou les bissectrices est en option.

Tu as toi-même amorcé la solution: le potentiel est la somme de 4 termes correspondant à chacune des pointes:
V_{(x, y)} = V_{1(x, y)} + V_{2(x, y)} + V_{3(x, y)} + V_{4(x, y)} ,
et en l'absence de charge d'espace, chaque terme vérifie ∆V_i = 0
tout en ne dépendant que de la distance du point du plan (M) à l'emplacement de la pointe (P_i .

Il faut au moins produire la figure de l'énoncé, avec les notations proposées.

[Martth]

Comme vous me l'avez conseillé voici un print screen de l'exercice
Mon problème c'est je ne sais pas comment retrouver les formes des equipotentiel. Si s'agissais de charges electriques dans le vide (ou un isolant) je saurais mais le fait qu'il s'agissent d'un differentiel de potentiel dans un conducteur je ne sais pas quelle equation utiliser.

Merci de votre aide

[A voir en vidéo sur Futura]

[penthode]

si le conducteur est considéré comme parfait ,

il n'y a pas de DDP , définition du conducteur

[gts2]

Si s'agissais de charges electriques dans le vide (ou un isolant) je saurais mais le fait qu'il s'agissent d'un differentiel de potentiel dans un conducteur je ne sais pas quelle equation utiliser.

Dans le conducteur j=gamma E et la conservation du courant donne le comportement de j(r), donc de E(r), il n'y a plus qu'à remonter au potentiel.
J'attends l'image pour savoir si on veut l'équation ou juste la forme des équipotentielles, parce que un contact ponctuel, cela risque de poser des pb de divergence.

[Opabinia]

On accordera une conductivité finie au milieu, pour que le problème soit soluble.

Il y a effectivement un problème aux point de contact, où l'on risque de trouver une densité de courant infinie. Cependant l'intitulé suggère qu'on se place à grande distance du centre.

[Opabinia]

On peut toujours, en attente du schéma, voir de quelle fonction potentiel il s'agit.

# Le domaine spatial est ici le plan euclidien, et la fonction potentiel de dépend que de deux variables de position; son laplacien admet donc pour expression:

∆V = (d²V/dx²) + (d²V/dy²) .

# Si de plus le point singulier se place à l'origine du repère, le système présente la symétrie de révolution autour de cette dernière, et le potentiel (V_M) ne dépend plus que de la distance (r = OM).

On envisage donc la fonction V = F(r),
complétée par l'expression de la distance r² = x² + y²
dont la différenciation 2r.dr = 2x.dx + 2y.dy
fait apparaître les deux dérivées partielles:

(dr/dx) = x/r ; (dr/dy) = y/r .

Il faut obtenir les expressions des deux dérivées partielles secondes:

(dV/dx) = F'(r).(dr/dx) = F'(r).(x/r) ;
(d²V/dx²) = F"(r).(x/r)² + F'(r)[1/r - (x/r²).(x/r)) = F"(r).x²/r² + (F'(r)/r³).(r² - x²) ;
(dV/dy) = F'(r).(dr/dy) = F'(r).(y/r) ;
(d²V/dy²) = F"(r).(y/r)² + F'(r)(1/r - (y/r²).(y/r)) = F"(r).y²/r² + (F'(r)/r³).(r² - y²)

puis celle du laplacien:

∆V = (d²V/dx²) + (d²V/dy²) = F"(r).(x² + y²)/r² + (F'(r)/r³).(2r² - x² - y²) = F"(r) + F'(r)/r .

En l'absence de charge d'espace, le potentiel vérifie la relation caractéristique des fonctions harmoniques:

∆V = 0

qui conduit à l'équation différentielle:

F"(r) = -F'(r)/r ;

On obtient par deux intégrations successives:

Ln(F'(r)) = Ln(K) - Ln(r) d'où: F'(r) = K/r ,

puis:

F(r) = K.Ln(r) - K.Ln(r°) = V°.ln(r/r°)

en retenant pour les deux constantes à introduire la forme la plus appropriée.

[gts2]

Pour le A) on demande uniquement un dessin, donc un raisonnement avec les symétries suffit
Les axes à 45° sont des axes d'antisymétrie de potentiel nul. Au voisinage des points on a des cercles (on oublie les autres), il suffit ensuite lorsqu'on s'éloigne de déformer un peu les cercles par continuité.

[harmoniciste]

Bonjour,
Juste par le bon sens, il me semble qu'en appliquant -V et +V sur deux sommets contigus seulement, l'équipotentielle 0 est la bissectrice du segment qui relie ces 2 sommets. Appliquant maintenant les potentiels -V et +V sur les deux autres sommets seulement, l'équipotentiel 0 est la même bissectrice. J'en conclue que par raisonnement symétrique, il existe deux équipotentielles 0 qui sont les axes à 45 °

[gts2]

Pour ce qui est du grand B) on a intérêt à utiliser le principe de superposition? Avec une électrode parcouru par I, on écrit la conservation du courant I=j*2*pi*r*e.
On additionne les quatre même si je suis pas sûr que cela serve à grand chose.

Pour le C) on revient au principe de superposition , ce qui donne un champ électrique en 1/r, puis E=-grad(V) qui conduit à un potentiel en ln(r), qui avec condition aux limites V(a)=V0 donne
Il ne reste plus qu'à additionner les quatre contributions.

[Opabinia]

Si les quatre pointes forment un carré de diagonale (2d), il faut les placer sur les bissectrices du repère afin de faciliter le calcul ultérieur du flux de courant (qui s'effectuera sur les deux axes); donc choisir les positions:

P₁ = (d' , d') ; P₂ = (-d' , d') ; P₃ = (-d' , -d') ; P₄ = (d' , -d')

après avoir posé: d' = d/2^1/2 .

Les équipotentielles forment un faisceau de trèfles à 4 feuilles dont les lobes occupent chacun des quadrants du repère, et entourent chacune des zones de contact. La figure présente deux axes de symétrie orthogonaux, (les bissectrices), et deux axes d'antisymétrie ((x'x) et (y'y)) les équipotentielles sont normales aux bissectrices.

Les lignes de courant joignent les points de contact opposés; elles présentent, loin du carré (r>>d), un contour en boucle ressemblant à celui des équipotentielles. Le seul cas de lignes droites est celui des bissectrices.
Elles sont toutes localement normales aux axes, qui constitueront le lieu d'intégration permettant d'accéder à l'intensité totale du courant.

Les conventions précédentes s'accordent facilement aux données de l'énoncé: l'expression du potentiel est

V = V°.Ln(r₁/r°) - V°.Ln(r₂/r°) + V°.Ln(r₃/r°) + V°.Ln(r₄/r°) ,

avec r° = a .

Il faut garder en tête les différents ordres de grandeur: e << a << d .

Je n'ai pas bien compris la légende, dans le cercle gris.

[Opabinia]

Vous avez sans doute repéré la coquille:

V = V°.Ln(r₁/r°) - V°.Ln(r₂/r°) + V°.Ln(r₃/r°) - V°.Ln(r₄/r°) ,

[gts2]

Allure des lignes de courant
courantSI.png

Allure des équipotentielles
potentielSI.png

[Opabinia]

On obtient par deux intégrations successives:
Ln(F'(r)) = Ln(K) - Ln(r) d'où: F'(r) = K/r ,
puis:
F(r) = K.Ln(r) - K.Ln(r°) = V°.ln(r/r°)
en retenant pour les deux constantes à introduire la forme la plus appropriée.

La fin de l'intégration (# 8) était un peu bâclée
F(r) = K.Ln(r) - K.Ln(r°) + K₁ = V°.ln(r/r°) + U
si F(r°)= U , conformément à l'énoncé.

Cela ne change cependant pas la suite des calculs.

# Du fait que l'on a: a << d ,
les points du petit cercle de rayon (r₁ = a = r°) centré en (M₁), qui présentent le potentiel (U), se trouvent
- à une distance de (M₂) et (M₄) ~ d.2^1/2 , et
- à une distance de (M₃) ~ 2d .
L'expression du potentiel total vérifie dans ces conditions:
V = U = (V°.Ln(a/a) + U) - (V°.Ln(d.2^1/2/a) + U) + V°.Ln(2d/a) + U - (V°.Ln(d.2^1/2/a) + U) = V°.Ln(a.2d/(d.2^1/2.d.2^1/2)) = V°.Ln(a/d) ,
ce qui permet la détermination de la constante (V°): V° = U/Ln(a/d) , d'où V° < 0 .

[Opabinia]

Le champ électrique E = - Grad(V)
se calcule à partir de l'expression simplifiée du potentiel

V = (V°/2).(Ln(r₁²) - Ln(r₂²) + Ln(r₃²) - Ln(r₄²)) ,

ainsi que des expressions des carrés des distances:

r₁² = (x - d')² + (y - d')²
r₂² = (x + d')² + (y - d')²
r₃² = (x + d')² + (y + d')²
r₄² = (x - d')² + (y + d')²

Il vient pour les dérivées partielles:

(dV/dx) = V°.((x - d')/((x - d')² + (y - d')²) - (x + d')/((x + d')² + (y - d')²) + (x + d')/((x + d')² + (y + d')²) - (x - d')/((x - d')² + (y + d')²)) ;

(dV/dy) = V°.((y - d')/((x - d')² + (y - d')²) - (y - d')/((x + d')² + (y - d')²) + (y + d')/((x + d')² + (y + d')²) - (y + d')/((x - d')² + (y + d')²)) ,

D'où une expression relativement simple du champ électrique

E = -(dV/dx)*u_x - (dV/dy)*u_y

sur chacun des axes;
a) sur l'axe (x'x), où y = 0 :

E_x = -V°.((x - d')/((x - d')² + d'²) - (x + d')/((x + d')² + d'²)+ (x + d')/((x + d')² + d'²) - (x - d')/((x - d')² + d'²)) = 0 ;
E_y = -V°.(-d'/((x - d')² + d'²) + d'/((x + d')² + d'²) + d'/((x + d')² + d'²) - d'/((x - d')² + d'²)) = 2V°d'.(1/((x - d')² + d'²) - 1/((x + d')² + d'²));

E est ici normal à (x'x).

b) sur l'axe (y'y), où x = 0 :

E_x = -V°.(-d'/(d'² + (y - d')²) - d'/(d'² + (y - d')²) + d'/(d'² + (y + d')²) + d'/(d'² + (y + d')²)) = 2V°d'.(1/(d'² + (y - d')²) - 1/(d'² + (y + d')²)) ;

E_y = -V°.((y - d')/(d'² + (y - d')²) - (y - d')/(d'² + (y - d')²) + (y + d')/(d'² + (y + d')²) - (y + d')/(d'² + (y + d')²)) = 0 .

E est ici normal à (y'y).

[gts2]

qui avec condition aux limites V(a)=V0 donne

Il faut bien sûr lire !
Corrigé après lecture du message de Opabinia.

[Martth]

Merci encore pour ces réponses .
@gts2 je ne suis pas sur d'ou tu sors le:



@Opanibia Ta dérivation de la solution est exacte, cepedant je trouve que cela manque un peu d'intuition physique. Je m'attarde tout de même sur ta solution! Merci

[gts2]

Les ri sont des coordonnées polaires d'origine le point i.

https://www.dropbox.com/s/7tp6cvjtcu...ur-si.pdf?dl=0

[gts2]

Une question : c'est un exercice académique ou cela correspond à la réalité ?
Le pb est que la solution dépend du rayon de contact de la pointe, ce qui me parait poser des pb de précision.
Les méthodes usuelles à quatre pointes séparent la partie alimentation (deux pointes dans lesquelles circulent I) et la partie mesure (deux pointes entre lesquelles on mesure la ddp), ce qui permet de s'affranchir du rayon de contact.

[gts2]

@gts2 je ne suis pas sur d'ou tu sors le:

Cette formule donne l'idée, mais elle est à corriger : lorsque je suis passé de scalaire à vectoriel j'ai "oublié" que , d'où un r manquant au dénominateur, et enfin il y a un e qui est passé à la trappe.

[Opabinia]

@ Martth

@Opanibia Ta dérivation de la solution est exacte, cependant je trouve que cela manque un peu d'intuition physique

Je ne vois pas bien ce que tu entends par là, mis à part l'établissement de l'expression générale du potentiel, qui était un peu confuse; je n'ai vu qu'après coup que la constante déterminante était le facteur V° = U/Ln(a/d) , de signe négatif en raison de l'inéquation a < d .

Les 4 termes sont de la forme V_i = ±(U + V°.Ln(r_i/a))
et vérifient V(a) = U au voisinage de la pointe positive.

Le signe des composantes du champ, dont l'expression a été établie sur les axes du repère et se ramène à une relation unique:

a) sur (x'x): E_y = 2V°d'.G(x) ,
b) sur (y'y): E_x = 2V°d'.G(y) ,

s'accorde avec l'orientation systématique du champ électrique (E) vers les potentiels décroissants, selon le schéma ci-dessous, très simplifié:

@ gts2: ton diagramme de distribution du potentiel paraît tourné de 45° par rapport au mien, et découle du placement des points de contact sur les axes, en (d, d), (-d, d), (-d, -d) et (d, -d).
L'idée est plus spontanée, mais les complications vont arriver ensuite, lors du calcul du flux de courant le long des deux bissectrices.

[gts2]

@ gts2: ton diagramme de distribution du potentiel paraît tourné de 45° par rapport au mien.

Oui, tout à fait, j'ai pris les mêmes conventions que le texte.

[Opabinia]

En effet, en y regardant de très près ...

Ce détail m'avait échappé.

[Opabinia]

L'intensité du courant correspond au flux du vecteur densité de courant j = γE à travers une surface entourant complètement les deux pointes positives (par exemple), ou à défaut allant à l'infini en recoupant toutes les lignes de courant.
La fonction étudiée V(x, y) ne dépendant pas de (z), les surfaces envisagées sont des cylindres de génératrices parallèles à (z'z) et de hauteur indéterminée - en pratique une bande verticale de largeur (e) située à l'intérieur de la couche semi-conductrice, de frontières (z₀ = 0 et z₁ = e).

La solution naturelle consiste à prendre les surfaces s'appuyant sur les axes du repère, c. à d. les bandes rectilignes basées sur les demi-droites (Ox, Oy) et (Ox', Oy').
Par raison de symétrie, chacune de ces quatre bandes est traversée par le même flux (I_ax) compté en valeur absolue; l'intensité totale du courant quadrupolaire admet par conséquent pour expression: I = 4.I_ax .

Le flux de courant à travers la bande s'appuyant sur la demi-droite (Ox) est:

I_ax = ∫₀ ^+∞j.dS = ∫₀ ^+∞γ│E_y│.edx = (-2V°)γe∫₀ ^+∞d'[1/((x - d')² + d'²) -1/((x + d')² + d'²)].dx

soit encore:

I_ax = (-2V°)γe.[Arctan((x - d')/d') - Arctan((x + d')/d')]₀^+∞ = (-2V°)γe.[-Arctan(-1) + Arctan(1)] = (-2V°)γe.[π/4 + π/4] = -πV°.γe .

On obtient finalement, compte tenu de la relation précédemment établie (V° = U/Ln(a/d)):

I = 4πV°.γe = 4πγe.U/Ln(d/a)

d'où l'expression de la résistance équivalente du système:

R = U/I = Ln(d/a)/4πγe .

.

Résultat à vérifier, naturellement. On doit retrouver la même chose à partir des conventions de gts2, strictement conformes à l'énoncé.

[gts2]

Résultat à vérifier, naturellement.

Je trouve la même chose, plutôt bon signe.