Dimensionnement d'un échangeur pour centrale hydraulique immergée

[Sopastom]

Bonjour,

N'ayant pas trouvé de problème similaire sur le forum, je vous expose le mien.

Une machine sous-marine est équipée d'une centrale hydraulique (alimentée en 3000V et consommant entre 50 et 100A). Or même sous l'eau, le moteur chauffe jusqu'à 137°C (T_max préconisée 150°C). C'est pourquoi j'aimerais dimensionner un système de refroidissement dans le circuit d'huile moteur. Pour faire simple, j'ai pensé à rajouter un échangeur tubulaire (en inox, et en serpentin ou pas, à déterminer) qui serait au contact de l'eau et dans lequel circulerait l'huile moteur afin d'être refroidie.
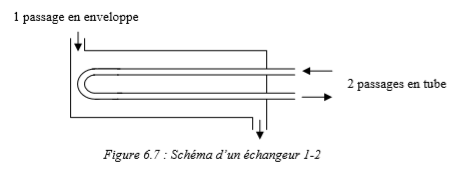
J'ai fait l'hypothèse d'un échangeur 1-2, en sachant que dans notre cas, il n'y aura pas d'enveloppe puisque l'échangeur sera à même le milieu environnant (l'eau):


J'aimerais donc trouver la surface d'échange nécessaire pour que l'huile ne dépasse pas les 100°C.

On note l'huile comme étant le fluide 1, et l'eau le fluide 2.
Données:
On connaît le volume d'huile dans le moteur V₁=40L ; le débit volumique dans le moteur Q_v=25L/min ; les températures huile et eau T_1,max=410K et T₂=283K. Concernant l'eau, on a pas d'autres données (température entrée ou sortie, débit)
On connaît les capacités thermiques massiques C_p1=4200J/kg/K et C_p2=2000J/kg/K ; la masse volumique de l'huile rho₁=983kg/m³ ; la viscosité cinématique de l'huile nu₁=32mm²/s ; on en déduit la viscosité dynamique mu ; la conductivité thermique de l'huile lamba₁=0.154W.K/m

Hypothèses:
Echangeur 1-2 "sans enveloppe"
Débit eau à peu près équivalent au débit d'huile (or je doute que celle-ci soit bonne, la machine travaille dans des réserve d'eau, des barrages, mais pourrait également travailler dans des canaux...)

J'ai donc appliqué la méthode de NUT avec ces données et je trouve NUT_max=0.376 (en prenant z=q_c1/q_c2=0.5 environ).
Le calcul du nombre de Reynolds donne: Re=4.rho.Q_v/(pi.D.mu) or il faut connaître le diamètre du tuyau. On fixe un diamètre de 15mm.
Re=1120.
Pour un régime laminaire dans la zone d'établissement thermique, on utilise la corrélation de Graetz qui donne un nombre de Nusselt environ égal à 20.
On en déduit le coefficient d'échange thermique h=lamba.Nu/D=205 et donc S=NUT_max.q_c1/h=1.5m² pour la surface d'échange.
Une telle surface correspondrait à une longueur de tuyaux de 31m...

Que pensez-vous du raisonnement ? Des valeurs trouvées ?
Si vous pouviez m'orienter sur les hypothèses/modèles thermodynamiques à suivre pour pouvoir bien dimensionner cet échangeur.

Ps: C'est un peu long mais je voulais expliquer clairement le problème.
-----

[RomVi]

Bonjour

Il manque la donnée la plus importante : Quelle est la puissance à dissiper ?

[Sopastom]

Il manque la donnée la plus importante : Quelle est la puissance à dissiper ?

On utilise la formule P=Q_m.C_p1.(T_1e-T_1s) ?
Ce qui donne P=((25.10^-3).983/60).2000.(137-100)=30,3kW

A partir de la puissance fournie et de la puissance dissipée peut-on établir un bilan énergétique ? Si c'est le cas, je ne vois pas comment retomber sur la surface d'échange nécessaire.
Ou sinon on ramène cette puissance au flux de chaleur, phi=lamba.S.(T_1e-T_1s)/e avec S la surface d'échange et e l'épaisseur du film (couche limite). Mais dans ce cas comment définir la valeur de cette épaisseur au sein d'une conduite ?

[RomVi]

Mais ces valeurs de débit et de température d'entrée et sortie viennent d'où ?

[A voir en vidéo sur Futura]

[Sopastom]

Le débit volumique donné correspond au débit d'huile dans le circuit du moteur hydraulique (c'est une donnée constructeur). La température en "entrée" de l'échangeur correspond à la température maximale que l'huile atteint lorsque le moteur est en fonctionnement (137°C, elle a été mesurée avec un capteur). La température en "sortie" correspond à la température souhaitée en sortie d'échangeur.
En fait j'aimerais que l'huile ne chauffe plus au-delà de 100°C en ajoutant un échangeur au niveau du circuit hydraulique du moteur.

[RomVi]

Je comprend mieux, malheureusement on ne peut pas utiliser cette approche.
Si la température maximale atteinte est actuellement de 137°C sans échangeur il n'y a sans doute pas grand chose à dissiper.
Comment le circuit d'huile est refroidit actuellement ?

[Sopastom]

Le moteur hydraulique est utilisé sous l'eau, il est donc constamment en contact avec l'eau (entre 8 et 20°C). Il est aussi équipé d'ailettes permettant, j'imagine, d'augmenter la surface d'échange.
Si un échangeur est connecté au moteur, la surface d'échange entre l'huile du moteur et l'eau environnante va augmenter et donc plus de chaleur va forcément se dissiper non ?

[RomVi]

Oui, le raisonnement est correct, c'est la démarche qui ne l'est pas.
Dans ce cas serait il possible d'estimer la surface d'échange actuelle ? Il sera ensuite possible d'extrapoler.

[Sopastom]

Le carter moteur est un cylindre de longueur 714mm et diamètre 384mm environ. La surface de ce cylindre est donc de 0,86m2, sans compter les ailettes dont je n’ai pas d’informations dans l’immédiat

Savez-vous par hasard quelle démarche suivre ? Personnellement j’ai ressorti mes cours de thermodynamique en essayant de trouver et de combiner le ou les modèle(s) qui se rapproche(nt) le plus du cas étudié (convection et écoulement dans une conduite, échangeur tubulaire...).

[RomVi]

Dans le cas d'un échangeur tubulaire plongé dans l'eau courante on se concentre sur le coefficient d'échange externe, qui généralement est limitant. Par sécurité on peut tout de même déterminer le coefficient d'échange interne, car le fluide étant de l'huile on peut avoir des surprises.
Par contre ici la démarche est très simple : Avec 0.86m² on a une température à l'équilibre de 137°C (avec un Dt moyen d'environ 120°C), donc pour atteindre une température de 100°C (un Dt de 80°C dans le cas le moins favorable) il faut une surface de 0.86 * 120/100 = 1.032m². En retirant la surface d'échange existante il faut ajouter 0.17m².

L'approche est un peu grossière, mais ce ne sera pas très éloigné de ce qu il faut.

[Sopastom]

Bonjour,
Si je suis votre raisonnement, il ne faudrait pas utiliser le Dt=80 plutôt que la température souhaitée de 100 degrés ?
Ce qui donnerait 0,86.120/80=1,29m2, soit une surface pour l’échangeur de 0,43m2 ?

[RomVi]

Oui effectivement c'est une erreur de ma part, il faut bien sur prendre 80°C de Dt.

[Sopastom]

Décidément je me prenais trop la tête.
Merci !