Bonjour,
J'ai le problème suivant à résoudre et je cale...
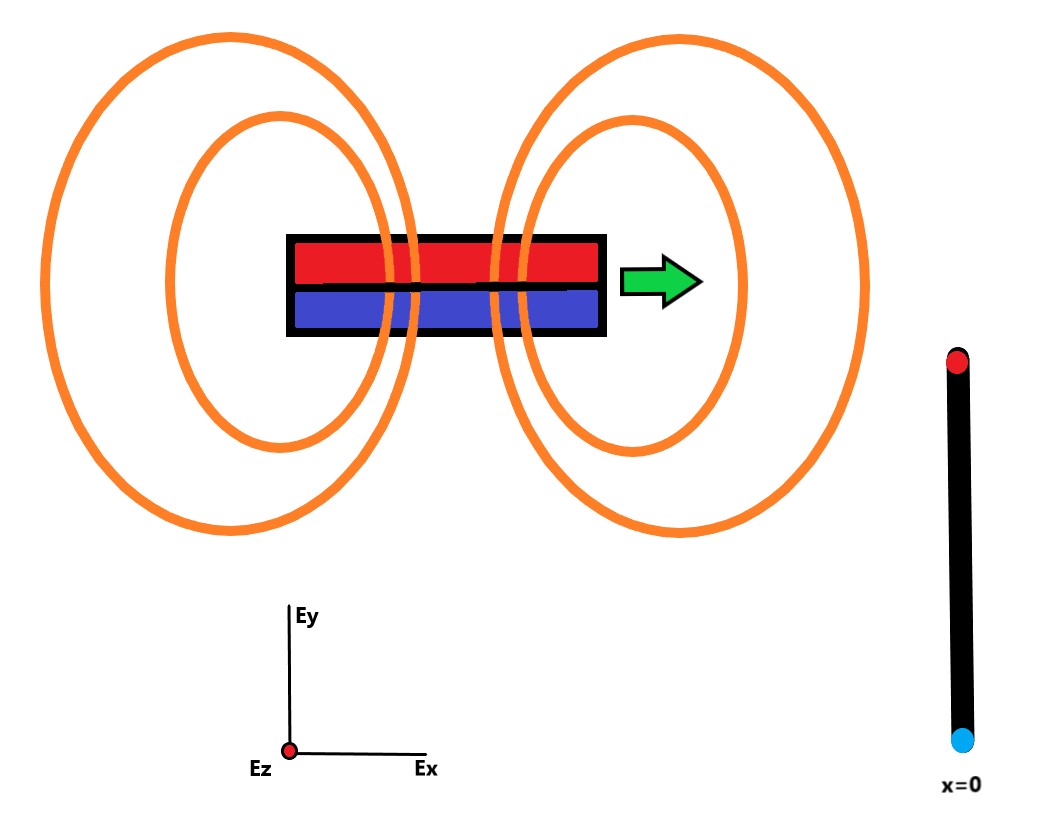
On a un aimant qui se déplace à une vitesse uniforme v = v0.Ex
Le champ magnétique B est comme représenté sur le dessin. Il va donc vers le bas et fait le tour de l'aimant à gauche et à droite pour remonter.
Il va passer juste au-dessus d'une spire fermée dont l'axe est orientée selon Ex.
Elle est donc dans le plan (Ey,Ez) positionnée en x = 0
Il faut tracer la forme du courant I(x).
Si c'est juste l'allure : étape 1 tracer les lignes de champ qui passent dans la spire (pour le signe), ceci avant et après.
En déduire l'allure de flux(t), puis l'allure de i(t).
Bonjour,
Il faut évaluer le flux magnétique dans la spire pendant le passage :
où sont les extremums, le minimum, quand varie t-il le plus vite.
Le courant à tracer est proportionnel à la dérivée du flux.
Comprendre c'est être capable de faire.
Selon moi, ou aurait :
En x = -inf : Phi = 0
En x ~ -L/2 : Phi = Phi_max
En x = 0 : Phi est nul
En x ~ L/2 : Phi = -Phi_max
En x = inf : Phi = 0
On en déduit :
En x = -inf, Phi est nul et constant -> I induit ~ 0
Entre x = -inf et x = -L/2, Phi grandit -> < 0
En x ~ -L/2, Phi est constant -> I = 0
Entre x ~ -L/2 et x ~ 0-, Phi diminue -> I > 0
En x ~ 0, Phi est constant -> I = 0
Entre x ~ 0+ et x = L/2, Phi diminue -> I > 0
Entre x = L/2 et x = inf, Phi tend vers 0 -> I ~ 0
Sur la fin, c'est plutôt
En x ~ L/2, Phi est min -> I = 0
Entre x = L/2 et x = inf, Phi diminue en valeur absolue mais augmente -> I < 0
Ensuite I -> 0
Ok pour vous ?
OK sauf autour de x=0, le flux passe en zéro avec une pente non nulle, j'aurai tendance même à dire que i est maximal par symétrie.
Oui. C'est correct...
Il n'est pas nécessairement maximum mais il est constant et non nul...
Tu as raison... En plus, il est bien max ! MERCI !!
