Portique Mécanique des Structures Déformables.

[ChateauLime]

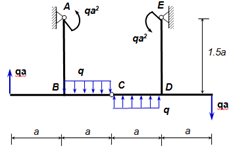
Bonjour, j'ai un portique à traiter. Il est présent ci-dessous :

La structure est symétrique par rapport au point C.
J'aimerais savoir si mes calculs et le raisonnement en général sont bons.

On commence par les réactions.
Le système comporte 4 réactions pour 3 équations, le système est donc hyperstatique d'ordre 1.

Concernant les équations, nous avons :

Somme des forces /x : Fx=Rha+Rhe=0 => Rha=-Rhe (Equation 1)

Somme des forces /y : Fy=Rva+Rve+qa-qa+qa-qa=0 => Rva=-Rve (Equation 2)

Somme des moments /A : -qa²+3qa²+qa²-qa²+1/2*qa²-1/2*qa²-Rve*2a=0 => 2qa²=2a*Rve => Rve=qa
D'après l'équation 2, on a alors : Rva=-qa

Somme des moments/C : Rva*a+Rha*1,5-qa²-1/2*qa²+qa*2a=0 => Rha*1,5a=3/2*qa²-(-qa²)=1/2*qa²
=> Rha=qa/3 +> D'après l'Equation 1, Rhe=-qa/3

Bilan : Rha=qa/3, Rhe=-qa/3, Rva=-qa et Rve=qa

On trace les diagrammes N, T et M.
Comme la structure est symétrique, on s'intéresse à la partie de gauche : de A->C.
On doit donc trouver les équations de chacune des sections.

Nous avons une section de A->B et une autre de B->C :

pour A->B, N=Rva T=Rha et M=-qa²+Rhax
pour B->C, N=-Rha, T=Rva-qx+qa et M=Rvax+Rha1,5a-qx²/2-qa²+qa(x+a)

Je ne suis pas sûr pour les réactions. Dans certains problèmes similaire à celui-ci avec la rotule sur Internet, ils ne prennent pas en compte les réactions de la rotule.
De plus, pour le moment entre B et C, j'ai un soucis : à cause de la force pa et de son moment engendré, je ne retrouve pas le moment de A-B quand x=a dans la section entre B et C quand x=0.

Merci de votre réponse.
-----

[Resartus]

Bonjour

Si la barre horizontale est homogène, tous les poids de ses quatre parties sont égaux, et tous vers le bas. Si je comprends bien c'est le qa (q étant le poids par unité de longueur)
Or, vous en avez mis certains vers le haut. Donc tous vos calculs et schémas de forces et de moments sont faux

En refaisant proprement vos équations, vous devez trouver que les réactions verticales en A et B sont égales et compensent tous ces poids
(en n'oubliant pas qu'il faut prendre aussi en compte les poids des supports verticaux*)

Vous allez retrouver aussi que les deux réaction horizontales sont opposées l'une à l'autre

Mais pour les calculer, il faudra prendre en compte la déformation non seulement de la partie centrale de la poutre horizontale , mais aussi celle des deux supports verticaux*
Et n'oubliez pas que le système est hyperstatique. Il y a des méthodes très précises dans votre cours pour les résoudre, que manifestement vous n'avez pas utilisées

*L'énoncé devrait préciser les caractéristiques de la poutre et des supports, mais si ce n'est pas le cas, il faudra sans doute supposer qu'lls sont constitués du même matériau et de même section

[ChateauLime]

Merci de votre réponse.
Dans notre cours, nous n'avons pas encore vu les méthodes de résolution de structure hyperstatique.
Notre enseignant nous a simplement dit que comme c'est symétrique on peut utiliser la moitié de la structure.
D'autres part, nous n'avons pas non plus abordé le point sur les déformations.

Par rappport à votre remarque sur le fait que les poids de ses quatres parties sont égaux, et tous vers le bas, aucune allusion là encore à cela dans le cours de notre enseignant.

Dans ce contexte, comment résoudre le problème d'une manière directe ?


Peut-être que le titre de mon sujet est trompeur, l'aspect vraiment déformable avec les équations des déformées, ... n'a pas encore été abordé.

En C, on a deux réactions donc en traitant uniquement la partie de gauche, on peut a priori s'en sortir : 3 équations (Somme des forces par rapport à x, y et somme des moments par rapport à A + Une équation des moments en C).

[Resartus]

Bonjour,
M'enfin, savoir que le poids d'un objet est une force toujours orientée vers le bas ne relève quand même pas des études supérieures!

Il y a bien une symétrie pour les forces en présence : très précisément une symétrie miroir, c'est pour cela que les composantes des forces perpendiculaires au miroir sont opposées (c'est le cas des réactions horizontales, tandis que celles qui sont dans le plan du miroir sont égales (c'est le cas des poids, et donc aussi des réactions verticales).

Ce qui est peut-être moins intuitif, et c'est peut-être de là que vient votre confusion, c'est pour les moments de ces forces. Comme ils résultent d'un produit vectoriel de forces par des distances, ils sont toujours opposés (car si la force est horizontale, elle se multiple par une distance verticale, et réciproquement).

Pour revenir à la prise en compte de la symétrie, on peut en effet conclure que la poutre est horizontale au point C, et se limiter au demi-dessin à droite, mais il va y avoir sur ce point C une réaction horizontale et un couple inconnus (pas de réaction verticale, car le point C n'est pas fixe : et il va de fait descendre un peu sous l'effet du poids de la poutre).
Et cela ne change pas le problème qui est toujours hyperstatique…Je ne comprends pas comment on peut vous donner ce genre d'exercice si vous n'avez jamais vu les méthodes de résolution adaptées.

Mais êtes-vous bien sûr que les liaisons sur les points B et D sont rigides? Parce que si ce sont des rotules (ou bien si les supports verticaux sont de simples fils), cela change tout, et cela devient le problème beaucoup plus simple d'une poutre horizontale encastrée en C, et soumise à des forces réparties (le poids de la barre) et ponctuelles (sur les suspentes)

Pourriez-vous nous donner le texte exact de l'exercice, sans le tronquer ni l'interpréter?

[A voir en vidéo sur Futura]