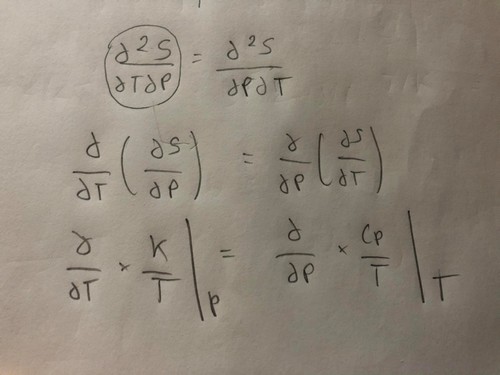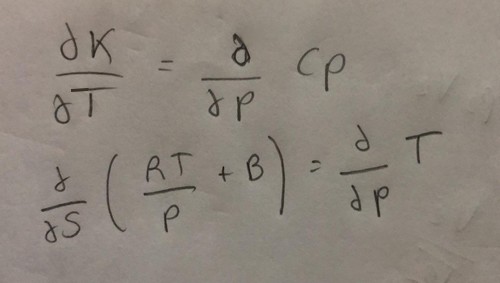Gaz réel thermodynamique

[Nestati]

Bonjour à tous j'ai un problème et je bloque car j'ai du mal à saisir l'énoncé de celui-ci
Il est dit l'équation d'état de l'azote entre 0 et 150 degré et 0 à 50 bar peut s'écrire P(V-B)=RT (1)
où B = b - β/𝑇^n (2)
avec b=32*10^-6, β=0.204, n=1.5, R=8.314 J/mole.K
Et la relation qui lie la capacité calorifique à pression constante pour une mole :
𝐶𝑝 = 30 + 35.5 × 10^−8𝑃 (3)
Il est demandé d'établir l'expression entre les variations de Cp (3) avec P et de B avec T (j'ai copié collé l'énoncé)
et ensuite de calculer la constante β de l'équation (2) et comparer à la valeur de l'énoncé 0.204.
Je sais qu'il faut s'aider des propriétés suivantes : dU et dS sont des différentielles totales exactes

J'ai du mal à comprendre ce que je dois exprimer en fonction de quoi.
En établissant l'équation différentielle totale de la viariation d'énergie interne

dU= (dU/dT)dT à v=cst + (dU/dV)dT à T=cst = Cv*dT
et
dS= 1/T(dU/dT)dT à v=cst + (1/T(dU/dV) à T=cst + P/T)dV

Avec Cp et dH/dT à P=cst
et Cv = dU/dT ) V=cst

Merci de votre aide
-----

[gts2]

Déjà, vu que vous utilisez Cp et que l'on vous demande les variations avec P, il est plus simple de partir de H et S.

Vous écrivez dH et dS en fonction des deux variables demandées P et T, pour T c'est connu, pour P vous posez un paramètre inconnu (à moins que vous n'ayez fait le cours dessus) disons que l'on pose
Et vous utilisez le théorème de Schwarz pour exprimer que dH et dS sont des différentielles.

[Nestati]

en partant de dH= TdS + VdP j'obtiens simplement dH = TdS + nRT(dP/P)
et dS= nCv dT/T + P/T ( nR/P dT - nRT/P² dP )
Sinon je vois pas trop

[gts2]

en partant de dH= TdS + VdP

Bon point de départ

j'obtiens simplement dH = TdS + nRT(dP/P)

Là vous avez appliqué la loi des gaz parfaits !

dS= nCv dT/T + P/T ( nR/P dT - nRT/P² dP )

1- c'est cp qui vous intéresse
2- évitez d'utiliser la loi des gaz parfaits pour un gaz réel.

Donc avec les bons paramètres dS=Cp dT/T + k/T dP
k inconnu mais pas grave, on a deux équations (dS et dH différentielles) pour trouver k et la relation Cp(P) / B(T) .

[A voir en vidéo sur Futura]

[Nestati]

Ma faute, dH = TdS + (RT/P + B)dP
donc dH = T(CpdT + kdP) + (RT/P +B) dP
Ensuite ?

[gts2]

Ensuite, il faut suivre l'indication du texte "dU (traduit en dH) et dS sont des différentielles totales exactes" et ma précision "utilisez le théorème de Schwarz"

[Nestati]

J'en suis arrivé à ce calcul pour dS mais comment poursuivre ?
Merci

[gts2]

Il faut faire la même chose avec dH et par combinaison entre les deux vous allez trouver k d'une part et dCp/dP d'autre part.

[Nestati]

J'arrive à ces deux équations mais je suis pas certain

[gts2]

L'image n'est pas encore validée, vous devriez trouver :

et

[gts2]

Je ne comprends pas trop comment vous obtenez vos équations :
la première est en contradiction avec celle que vous avez obtenu à partir de dS : (1) : où est passé k/T ?
la deuxième n'utilise pas les bonnes variables T et P et le deuxième membre est nul.

Avec dH, vous avez du obtenir (2)
(1) et (2) sont très proches et il est donc facile d'obtenir k.

Ensuite, il faudra bien faire intervenir la loi du gaz pour calculer

[Nestati]

avec V= nRT/P je trouve que dV/dT = nR/P et donc que K= -nRT/P soit = -V

[gts2]

Oui c'est bien cela si k=-V, alors TdS=CpdT-VdP, soit TdS+VdP=CpdT=dH 2ème loi de Joule des gaz parfaits.

C'est juste, mais j'avais cru comprendre qu'on s'intéressait au gaz d'équation P(V-b +β/Tⁿ)=RT

[Nestati]

Oui en effet
Après changement d'équation j'obtiens dV/dT = nR/P + nβ/T^(n+1)

[gts2]

C'est bien cela mais enlever le premier n (R/P et non nR/P) : l'équation donnée est celle d'une mole et on risque de confondre avec le n de Tⁿ.

[Nestati]

J'obtiens que K = -V -nβ/T^n
et donc que dCp/dP = n²β/T^(n+1) + R/P + nβ/T^(n+1)

[gts2]

J'ai l'impression que vous faites toujours la même erreur :
, d'accord mais P/RT n'est pas égal à V (çà c'est le gaz parfait)