Bonjour,
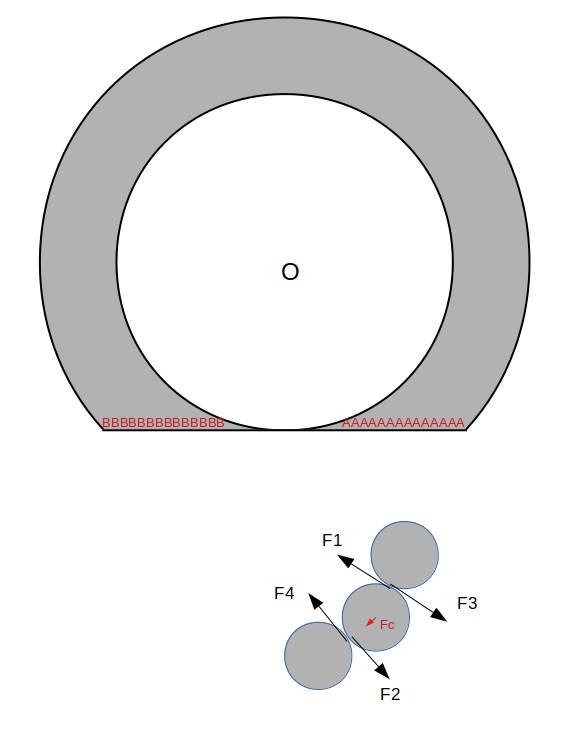
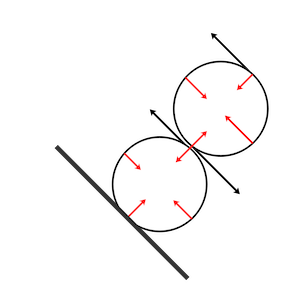
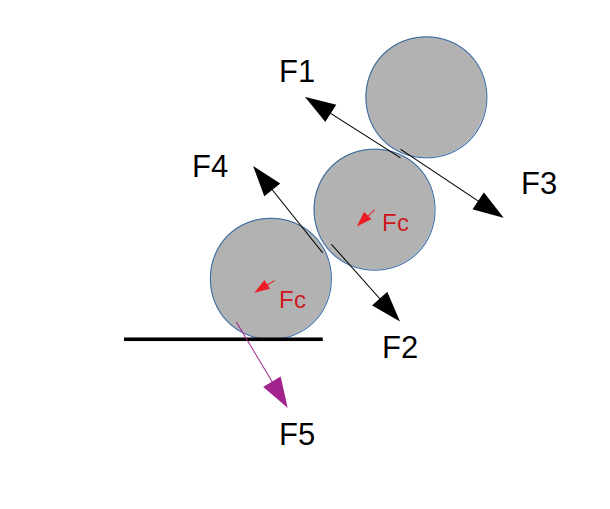
J'ai une géométrie où je n'arrive pas à trouver la somme des forces à 0. C'est une géométrie assez simple et les deux gradients de pression sont perpendiculaires, mais je dois prendre une mauvaise pression car je ne sais pas comment calculer de manière générale la force de pression lorsqu'il y a plusieurs gradients de pression. Vous savez ? Je peux expliquer la géométrie si c'est nécessaire, dites moi.
Bonne journée à tous.
BL
Bonjour,
Un dessin ou une description serait utile, sinon les gradients c'est linéaire, donc si vous avez deux gradients, le gradient résultant est la somme des deux (la dérivée d'une somme est la somme des dérivées).
On ajoute les gradients de manière scalaire ou vectorielle ?
Voilà pour la géométrie:
La couleur grise est l'équivalent d'un fluide. Donc il y a une multitude de sphères à l'intérieur du récipient. Les parois noires sont fixes. Un dispositif externe insère des sphères en "AAAAAAA" et les sors en "BBBBBBB", ceci perpendiculairement à l'écran. Les sphères ont toutes la même vitesse angulaire autour de 'O' et il n'est pas nécessaire d'en insérer beaucoup, c'est juste pour avoir les forces comme je l'ai dessiné. Il y a de la friction entre les sphères uniquement comme je l'ai dessiné: forces F1, F2, F3, F4, etc. car les sphères ne tournent pas sur elles mêmes et comme elles tournent autour de 'O' sens trigo alors elles tournent l'une vis à vis de l'autre en sens horaire. Sur chaque sphère il y donc une force "Fc" qui a la direction de la tangente, c'est le premier gradient de pression, il est circulaire. La paroi circulaire interne du récipient (petit cercle) a un gradient de pression qui va de 0 à 2pi (à multiplier par un facteur). La paroi circulaire externe, ne va pas de 0 à 2pi, pour un rayon donné, la paroi interne a plus de pression que la paroi externe, donc il y a un deuxième gradient de pression, qui est radiale cette fois. Bien entendu il y a des forces de pressions sur la paroi horizontale (le segment). Je m'intéresse à la somme des forces horizontales car je ne trouve pas 0, j'ai bien entendu ajouté les forces "terminales" que le dispositif externe doit donner aux sphères de "bout" en "AAAAAAA" et "BBBBBBB" pour avoir sur chaque sphère la force "Fc".
Si c'est pas assez clair, je peux réexpliquer sans problème.
Pour ce qui est du gradient, explicitement,
Sinon pourquoi vous attendez-vous à une résultante de pression horizontale nulle ? C'est peut-être la résultante totale qui est nulle en prenant en compte les frottements ?
"les sphères ne tournent pas sur elles mêmes et comme elles tournent autour de 'O' sens trigo alors elles tournent l'une vis à vis de l'autre en sens horaire"
Pourriez-vous préciser : si les sphères sont en translation circulaire, alors elles ne tournent pas "l'une vis à vis de l'autre".
Avez-vous une expression des deux gradients, ou est-ce numérique ?
A la question de la résultante de pression horizontal nulle, je suis parti du fait que la somme des forces est toujours nulle, donc elle l'est sur l'axe horizontal aussi. J'ai calculé la somme des forces venant des parois et les forces "terminales" que le système externe doit donner aux sphères en "AAAAAAA" et "BBBBBBB". Ensuite, chaque sphère possède une somme des forces nulle puisque s'il y a "Fc" sur chaque sphère, il y a aussi un équivalent de la poussée d'Archimède et donc chaque sphère a une somme des forces nulle. J'ai supposé que l'équivalent de la poussée d'Archimède agit en fonction des 2 gradients de pression.
Pour la précision: si les sphères sont en translation circulaire...: le système externe empêche que les sphères ne tournent sur elles-mêmes, est ce votre question ?
Oui, j'ai une expression du gradient: c'est une fonction de l'angle et de la force de friction. Je peux développer si nécessaire.
Pour ce qui est de votre expression du gradient, c'est la définition générale ou celle appliquée à ma géométrie ? J'ai quelques difficultés à saisir votre équation.
"la somme des forces est toujours nulle" : si vous prenez comme système le tuyau immobile, on peut très bien imaginer qu'il y a un support (et je suppose qu'il existe) donc 0=F(billes->tuyau)+F(support->tuyau)
La sphère a un mouvement circulaire, donc la somme des forces n'est pas nulle.
"le système externe empêche que les sphères ne tournent sur elles-mêmes" OK
Pour le gradient cela signifie que vous connaissez dp/dr (radial) et dp/d\theta "circulaire" et vous cherchezou plus exactement
Vous dites que la somme des forces n'est pas nulle à cause du mouvement circulaire des sphères, ceci à cause de la masse ? mais je peux considérer la masse quasi nulle pour m'éviter des calculs complexes, ou si faible que la masse n'intervient plus. Dans ce cas il faut bien que la somme de toutes les forces soit nulle, oui en prenant en compte le support car il y en a un. Je compte les forces dues à la pression sur les parois, je compte la réaction des forces que le système externe doit donner aux sphères limites en "AAAAAAA" et "BBBBBBB". La somme des forces sur chaque sphère est-elle bien nulle à cause de l'équivalent de poussée d'Archimède comme je le suppose ?
Ce que vous appelez "tuyau" ce sont mes parois en vue en coupe ?
Pour le calcul des forces de pression sur les parois circulaires externe et interne, je n'ai considéré que le gradient circulaire, je n'ai pas pris en compte le gradient radial car il est toujours perpendiculaire. Je peux donner les calculs que j'ai effectué mais si la méthode n'est à la base pas bonne il vaut mieux que je les refasse avec la bonne méthode.
"Ce que vous appelez "tuyau" ce sont mes parois en vue en coupe ? " Oui
"je n'ai pas pris en compte le gradient radial car il est toujours perpendiculaire". Vous l'avez pris en compte puisque vous dites que "la paroi interne a plus de pression que la paroi externe", cela c'est le le gradient radial.
Mais en intégrant sur une paroi à r constant, par définition P(r=Cte,\theta) ne dépend que de \theta, si c'est ce que voulez dire, on est d'accord.
Vous dites qu'on peut négliger la masse des billes, pourquoi pas.
Le gradient de pression vient des forces de contact ?
Oui, j'ai constaté qu'il y a un gradient de pression radial mais pour calculer la force provenant de la pression sur les parois je ne tiens compte que du gradient circulaire qui est différent, pour un angle donné, pour chaque paroi curviligne (interne/externe). Oui, cela dépend de \theta.
Le gradient de pression circulaire provient des forces de friction entre les sphères, chaque force '"Fc" sur chaque sphère. Il y a un gradient de pression radial parce que la paroi externe "démarre" plus tard (au niveau de l'angle) que la paroi interne.
En revenant à la question de départ, si vous négligez la masse des billes, vous aurez bien F=0 mais il y a d'une part les forces de pression et d'autre part les forces de frottements, c'est la somme des deux qui doit être nulle.
La somme des deux ? les frottements entre les sphères donnent les forces "Fc" sur chaque sphère, l'équivalent de la poussée d'Archimède annule les forces "Fc" sur chaque sphère. Il reste les forces sur les parois provenant de la pression et la réaction parce que le système externe applique les forces aux sphères terminales (pour avoir Fc aussi sur les sphères terminales). Selon vous, les forces "Fc" doivent être comptées ?
Au niveau du contact paroi sphère, les forces de frottement (l'équivalent de F1 2 3 4 entre sphères) existent aussi, non ? Sinon les sphères du bord ne respecteraient pas F=0.
Non, il n'y a pas de friction entre les parois et les sphères. La friction est juste entre les sphères pour avoir les forces "Fc" et bien sûr il faut ajouter les forces des sphères terminales en "AAAAAAA" et "BBBBBBB". Ce que vous appelez les sphères du bord ce sont du bord des parois ? Je ne comprends votre dernière phrase: Sinon les sphères du bord ne respecteraient pas F=0.
Prenons la sphère en bas de votre dessin soumise à F4 et supposons qu'elle soit en contact avec la paroi, F=0 sur cette sphère va donc donner un cas particulier puisque contrairement à la sphère au-dessus soumise à F2 et F1, il n'y a pas l'équivalent de F2. Quelle est la conséquence de ce cas particulier ? gradient de pression élevé aux parois ?
Le système externe donne les forces qui manquent aux sphères terminales (uniquement les sphères en "AAAAAAA" et "BBBBBBB") pour avoir justement juste "Fc" même sur ces dernières sphères. Comme cela le gradient de pression est toujours valable. Dans ma somme des forces horizontales, j'ai tenu compte de la réaction de ces forces que le système externe doit exercer.
OK frottement entre sphères et pas sur la paroi, mais si on regarde la sphère du bas sur la paroi comparée à la sphère du haut, F=0 va engendrer un gradient de pression (rouge) nettement plus important au bord qu'au milieu, puisque cette fois il n'y pas les deux forces de frottement qui se compensent presque ?
Autre remarque, on a quand même l'impression qu'il y a un moment et les sphères ne tournent pas ?
Dernière modification par gts2 ; 28/11/2020 à 17h59.
Il y a un moment sur chaque sphère mais ce moment est annulé par le dispositif externe pour ne pas qu'elles tournent et que justement il y ait bien les forces de friction entre sphères.
La force F5 est ajoutée par le dispositif externe:
Donc toutes les sphères ont "Fc" comme somme des forces. Pour vous, le gradient n'est pas le même aux bords ?
Si vous avez F5 qui est appliquée, pas de problème.
Et dans ce cas somme des forces=0 concerne {paroi, dispositif externe}
Cela ressemble à quoi "en vrai" ce dispositif externe ?
Dans mes calculs je ne trouve pas du tout la somme des forces horizontale à 0. Avec R1 le rayon interne et R2 le rayon externe, F la force de friction entre les sphères (la même valeur pour toutes):
La force horizontale sur la paroi interne: -2piFR1
La force horizontale sur la paroi externe: R2*intégrale de (y-x)*sin(y) dy de x à 2pi-x avec x = acos(R1/R2)
La force de réaction due aux forces terminale (comme F5) : 2*intégrale de sin(atan(y/R1)) dy de 0 à R2*(pi/2-x)
J'obtiens pas 0. Si la méthode n'est pas en cause c'est sans doute mes calculs.
Sans détails, on a du mal à comprendre les calculs :
Exemple : La force horizontale sur la paroi interne:
Peu importe le nombre de sphères, l'angle et donc la force "Fc" va changer en fonction de la taille. Vous pouvez reprendre l'intégrale de la paroi externe si vous voulez.
OK, et donc le fait que cela ne soit pas homogène à une force ?
Oui, bien vu, mais la pression est une fonction de l'angle comme vous l'avez indiqué plus haut (et aussi de la force) donc le 2piF représente une pression (par unité de longueur) et non une force.
Je ne suis sûr d'être d'une grande utilité, je raisonnais par analogie avec un fluide visqueux dans un tuyau, cela n'a pas l'air d'être très pratique.
J'ai un peu de mal à suivre, par exemple votre F5 existe sur tout le pourtour, j'ai l'impression que vous ne sommez que sur la base.
Si, vous m'aidez à me poser des questions auxquelles je n'avais pas pensé comme l'homogénéité dans le calcul de la force. Comme vous m'avez posé la question de la somme des moments, j'y ai regardé et idem je ne trouve pas 0.
Effectivement, pour le calcul de F5, mon calcul ne tient pas compte de la densité du nombre de sphères, si j'ai 100 sphères sur le segment horizontal, la somme des forces sur l'horizontal ne sera pas la même que si j'ai 1000 sphères. Cela ne pose pas de problème sur le calcul du gradient circulaire. Je vais y réfléchir.
Je pense que je dois tenir compte de la taille des sphères et donc les calculs deviennent:
La force horizontale sur la paroi interne: -2piFR1/(2r)
La force horizontale sur la paroi externe: R2/(2r)*intégrale de (y-x)*sin(y) dy de x à 2pi-x avec x = acos(R1/R2)
La force de réaction due aux forces terminale (comme F5) : 2/(2r)*intégrale de sin(atan(y/R1)) dy de 0 à R2*(pi/2-x)
avec r le rayon des sphères. C'est logique pour le calcul des forces à donner sur les sphères terminales mais finalement même sur les parties curvilignes, la pression est une fonction de l'angle et de la force F mais plus j'ai de sphères et plus j'ai de forces sur les parois. Mais cela ne change pas la somme.
Si on connaissait les tenants et aboutissants du problème, on pourrait peut-être un peu plus répondre.
C'est un dispositif concret du type : sphères sur une couche qui s'écoulent entre deux parois ?
C'est une modélisation d'écoulement de grains ?
C'est une modélisation d'un fluide particulier ?
On vous a fourni un début de modélisation et vous complétez, ou la modélisation est fournie et il faut que vous en tiriez quelque chose ?
...
C'est un dispositif concret, une couche suffit. C'est une question que je me pose pour comprendre comment calculer les bonnes pressions dans ce genre de problème.
