Calcul de force dans un vérin

[gabrieldom]

Bonjour,

Je dois résoudre ce problème et je m'empêtre dans les calculs.

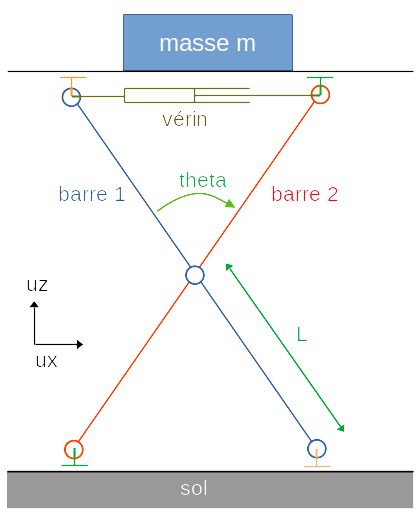
Tout se place dans le plan (ux, uz).
Une masse m est posée sur un plateau horizontal, qui est porté par un croisillon. Les deux barres du croisillon sont liées au milieu par une liaison pivot, et sont liées par leurs extrémités au plateau et au sol par des liaisons sphère-plan (ou pivot + glissière).
Un vérin permet de contrôler l'écartement des deux barres, sur l'axe ux, à leurs extrémités supérieures.
Exprimer la force que doit exercer le vérin pour retenir les deux extrémités, en fonction de theta.

J'ai commencé le bilan de forces :

• Poids exercé en C : P1=-mg/2 * [uz] en C
• Poids exercé en D : P2=-mg/2 * [uz] en D
• Force exercée par le vérin sur la barre 1 : F1=F*[ux] en C
• Force exercée par le vérin sur la barre 2 : F2=-F*[ux] en D
• Force exercée par le sol sur la barre 1 : R1=+mg/2 * uz]
• Force exercée par le sol sur la barre 2 : R2=+mg/2 * uz]

Je pensais faire le bilan de moment en O, qui doit être nul lorsque le système ne bouge pas. On a alors :
Mo([P1])+Mo([P2)+Mo([F1])+Mo([F2])+Mo([R1])+Mo([R2]) = 0
donc [OC]^-mg/2 [uz] + [OD]^-mg/2 [uz] + [OC]^F*[ux] + [OD]^-F*[ux] + [OA]^mg/2 [uz] + [OB]^mg/2 [uz] = 0
or [OA]+[OB] et [OC+OD] sont 2 vecteurs verticaux (selon uz) donc ([OA]+[OB])^mg/2 [uz] = 0 et [OC+OD]^-mg/2 [uz] = 0

Il me reste [OC]^F*[ux] + [OD]^-F*[ux] = 0, ce qui ne me sert à rien !

Sauriez-vous m'aider ? Je ne vois pas bien comment m'en sortir...

Merci d'avance


-----

[Tifoc]

Bonsoir,
Isolez une demi-barre (supérieure)

[Tifoc]

La nuit porte conseil : idolez une barre (complete)

[gabrieldom]

Bonjour,
Merci de votre réponse !

J'ai réessayé avec cette méthode.

Bilan de forces :
Poids exercé en C : [P1]=-mg/2 * [uz] en C
Poids exercé en D : [P2]=-mg/2 * [uz] en D
Force exercée par le vérin sur la barre 1 : [F1]=F*[ux] en C
Force exercée par le vérin sur la barre 2 : [F2]=-F*[ux] en D
Force exercée par le sol sur la barre 1 : [R1]=+mg/2 * [uz]
Force exercée par le sol sur la barre 2 : [R2]=+mg/2 * [uz]
Force exercée par la barre 2 sur la barre 1, et réciproquement : [F(2->1)]=-[F(1->2)]

Soit deux vecteurs unitaires [u1] et [u2] situés dans les axes des barres 1 et 2, dirigés vers le bas.

Isolons la barre 1 : [F1]+[R1]+[F(2->1)]=0
Projetons sur [u1] : mg*cos(theta/2)+F*cos(Pi-Pi/2-theta/2)+[F(2->1)].[u1]=0
Isolons la barre 2 : [F2]+[R2]+[F(1->2)]=0
Projetons sur [u2] : mg*cos(theta/2)+F*cos(Pi-Pi/2-theta/2)+[F(1->2)].[u2]=0

Je suppose que [F(2->1)].[u1]+[F(1->2)].[u2]=0 (mais je ne sais pas comment le montrer).

J'obtiens, en sommant les deux équations : 2*mg*cos(theta/2)+2*F*sin(theta/2)=0
soit : F=-mg*cos(theta/2)/sin(theta/2)=-mg/tan(theta/2)

C'est un peu contre-intuitif :
- le vérin doit pousser (signe "-") les barres vers l'extérieur plutôt que les rapprocher
- si theta tend vers Pi, la force devient nulle, et si theta tend vers 0, la force devient infinie... j'aurais plutôt imaginé l'inverse !

[A voir en vidéo sur Futura]

[Tifoc]

C'est un peu contre-intuitif

C'est surtout faux

j'aurais plutôt imaginé l'inverse !

Vous devriez faire un peu plus confiance à votre intuition

Bon sérieusement, isolez la barre 1, elle est soumise à 4 forces dont deux entièrement connues et parallèles, une de direction connue et perpendiculaire aux deux autres, écrivez l'équation de moment au point d’application de la quatrième (le centre du croisillon) et hop, c'est fini