Théorie des moments pour rotor caréné

[Nekama]

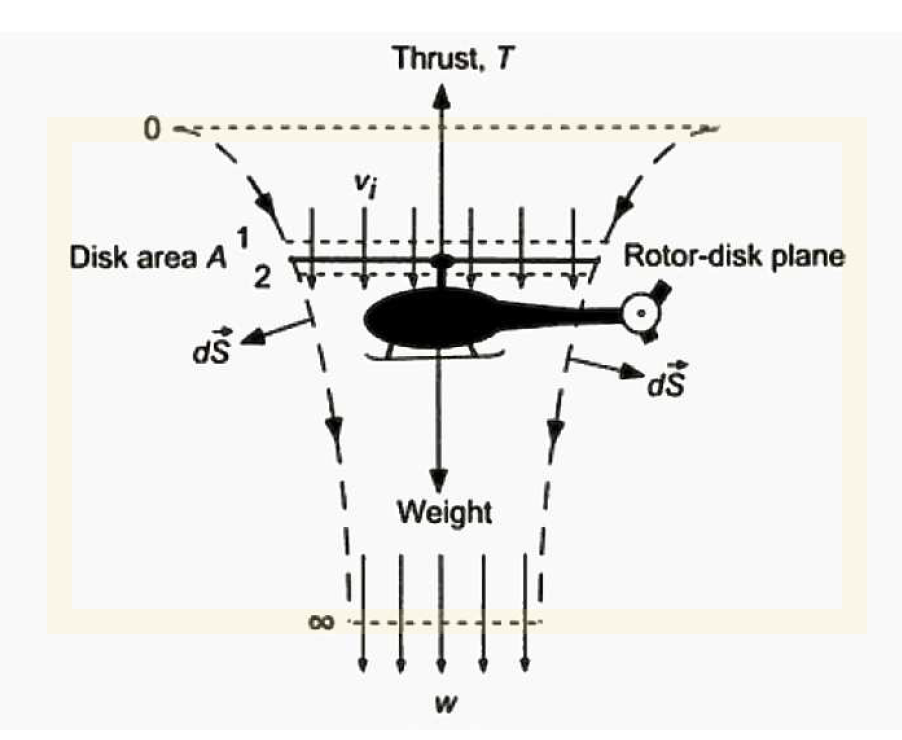
Bonjour à tous,

J'essaie d'appliquer la théorie des moments à un rotor (d'hélicoptère) caréné.
Je me demande si ce que j'écris est correct et sinon, si qqn pouvait corrigé mon calcul et/ou raisonnement.

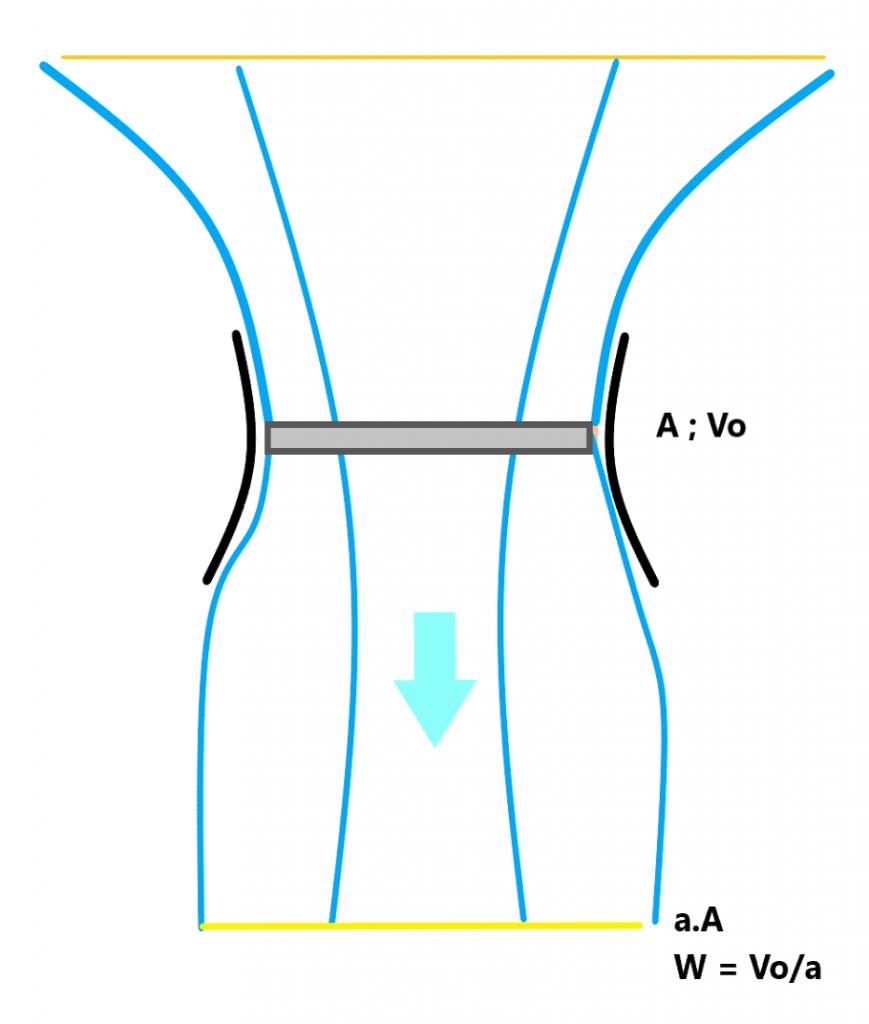
La vitesse induite à l'air au niveau du rotor est Vo.
Le rotor agit sur une surface A.
La forme du carénage est telle que l'air sort à une vitesse W = Vo / a
On note rho, la densité de l'air.

La Poussée de l'air sur l'ensemble vaut :

T = m'.W = rho.A.Vo.W = rho.A.Vo^2 / a (1)

La Puissance idéale nécessaire vaut :

P = T.Vo = rho.A.Vo^3 / a (2)

Le rapport T/P vaut donc :

T/P = 1 / Vo (3)

En tirant l'expression de Vo en fonction de P de l'expression (2), on obtient :

T/P = ( rho.A / P.a )^1/3

J'en déduis qu'à densité rho, puissance P et surface A égales,
le rapport Poussée / Puissance T/P est d'autant plus grand (et donc meilleur) que a est petit.

On en conclut donc que le rajout d'un carénage (même de masse négligeable) augmente la puissance à fournir pour une même poussée P (ou puisqu'il s'agit d'un rotor d'hélicoptère pour un même poids à sustenter) puisqu'il empêche (ou diminue) la contraction de l'air.

-----

[gts2]

Pour la conclusion, un carénage augmente bien la puissance à fournir.

Pour les calculs par contre, j'ai du mal à comprendre : d'où vient T = m'.W ?

[f6bes]

On en conclut donc que le rajout d'un carénage (même de masse négligeable) augmente la puissance à fournir pour une même poussée P (ou puisqu'il s'agit d'un rotor d'hélicoptère pour un même poids à sustenter) puisqu'il empêche (ou diminue) la contraction de l'air.
Pièce jointe 436147

Bjr à toi,
Ca c'est bien pour l'ascension!
Mais comment qu'on fait pour se déplacer....horizontalement ?
Le carénage empéche le les pales du rotor de "mordre" dans l'air ! (déplacement latéral)
Ne pas oublier que les pales sont la aussi pour avancer( ou reculer) l'engin.
Bonne journée
Bonne journée

[Nekama]

Merci pour le réponses.

Avec le W pour vitesse, ce n'est pas très lisible.
C'est : F = dp/dt = d(m.v)/dt = d(m)/dt . v = m'.W

Mon soucis est que la conclusion est le contraire de ce que je lis dans Leishman, 'Principles of helicopter aerodynamics', 2006, p.326

Il dit que pour une même poussée, la puissance à fournir est plus petite avec un carénage (a > 1) que sans (a = 1/2).

Je conclus pile l'inverse.

[A voir en vidéo sur Futura]

[calculair]

Bonjour,

Cela ne m'étonne pas .....

La theorie de Bernoulli appliquée à une hélice me donne des résultats avec une erreur de plus de 50%

D'apres ce que j'ai lu sur les carénages , il faut que l'hélice passe tres près du bord du carénage. Le gain est lié à la réduction des tourbillons en bout de pale.

Par contre je n'ai aucune idée comment démontrer cela avec les équations .....

Merci pour le réponses.

Avec le W pour vitesse, ce n'est pas très lisible.
C'est : F = dp/dt = d(m.v)/dt = d(m)/dt . v = m'.W

Mon soucis est que la conclusion est le contraire de ce que je lis dans Leishman, 'Principles of helicopter aerodynamics', 2006, p.326

Il dit que pour une même poussée, la puissance à fournir est plus petite avec un carénage (a > 1) que sans (a = 1/2).

Je conclus pile l'inverse.

Pièce jointe 436168

[gts2]

C'est : F = dp/dt = d(m.v)/dt = d(m)/dt . v = m'.W

d(mv)/dt ne donne pas dm/dt.v : c'est un système ouvert : il faut prendre +mv en aval et -mv en amont. Voir par exemple : wikibooks

[Nekama]

Yeap ! C'est vrai que le carénage permet d'éviter les tourbillons en bout de pâles si la distance entre le carénage et le bout de pâle est faible.
Dans les équations, les auteurs rajoutent un facteur correctif (B ~ 0.96) dans le calcul du C_T (Thrust Coefficient) pour en tenir compte.

Le problème est ici vraiment théorique. D'ailleurs, il faudrait noter P_id plutôt que P

Mais Leishman en est bien conscient.
On est dans un calcul théorique de physique ici.

[Nekama]

d(mv)/dt ne donne pas dm/dt.v : c'est un système ouvert : il faut prendre +mv en aval et -mv en amont. Voir par exemple : wikibooks

Ok. Oui.

Dans la théorie des moments (et c'est ce que font tous les auteurs), on considère l'apport en amont comme nul car la vitesse est nulle.
C'est ce que fait Leishman aussi. Pas de soucis à de niveau.

Le calcul correspond bien à ta remarque.

W est la vitesse en bas du carénage dans la veine "stationnaire" (cf. le schéma du 1er post)

On calcule le débit m' au niveau du rotor et on utilise W, pas Vo

[Nekama]

Le schéma ci-dessous (sans carénage) illustre comment la 'théorie des moments' est utilisée pour les hélicoptères.
On peut démontrer que W = 2 Vo dans ce cas.

Le carénage permet d'avoir une veine inférieure moins contractée et W = Vo/a.

Ma question est de savoir si cela diminue (mon calcul) ou augmente (Leishman) le rapport T/P

[harmoniciste]

Bonjour,
L'effet principal d'un carénage n'est pas dû à la suppression des tourbillons marginaux en bouts de pales. Il est dû aux pressions aérodynamiques s'appliquant sur les surfaces propres du carénage

[Nekama]

Ma question ne se veut pas "pratique" mais bien théorique sur le principe de calcul par la théorie des moments. C'est le contexte dans lequel Leishman se place également. (En prenant l'hypothèse que la qtt de mvt via l'entrée d'air dans le système est nulle ce qui conduit à une poussée induite par son éjection en dessous du rotor. On a un fluide compressible supposé parfait.)

Je ne comprends pas comment il peut arriver à dire que le rajout d'un carénage augmente le rapport poussée / puissance alors que le calcul me semble montrer que c'est l'inverse (et qu'en tout cas la conclusion semble bonne et donc celle de Leishman fausse a priori).

Je ne comprends pas la remarque relative aux pressions aérodynamiques sur le carénage. C'est la poussée seule dont il est question et on peut supposer le carénage droit (un bout de cylindre vertical) et sans frottement (fluide parfait).

Je mettrai le calcul de Leishman en ligne pour la différence de raisonnement mais je pense plus neutre de d'abord "conclure" sur le calcul et la conclusion qui en découle.

[harmoniciste]

Je ne comprends pas la remarque relative aux pressions aérodynamiques sur le carénage. C'est la poussée seule dont il est question et on peut supposer le carénage droit (un bout de cylindre vertical).

Peut-être devez-vous éclaircir votre idée de "poussée seule".
Si vous sous-entendez "poussée de l'hélice seule" alors un carénage droit ne changera quasiment rien, sauf la suppression des pertes marginales
Une différence de poussée totale (Hélice + carénage non droit) provient essentiellement de la poussée qui s'applique sur les parties "non-droites" du carénage.

[Nekama]

Effectivement... Avec la carénage que vous proposez, on a une poussée vers le haut supplémentaire avec un effet de portance (et aussi une poussée supplémentaire vers le bas avec la traînée mais a priori moindre).

Cela me fait penser que dans le cas étudié par Leishman (cf. mon dessin au premier post), on a encore une poussée négative supplémentaire sur la partie basse du carénage due à l'évasement.

Mais ma question porte sur la contraction de la veine et je cherche bien la poussée totale sur le rotor (et son carénage) avec l'effet de contraction (ou de non-contraction) de la veine qui nait suite au carénage car pour moi, on a :

T/P = ( rho.A / P.a )^1/3

et donc si a augmente, T/P diminue à P constant.

[harmoniciste]

Bonjour,
Je pense qu'il y a une confusion dans votre raisonnement.
En vol stationnaire, V₀ de votre croquis est la vitesse induite au droit de l'hélice. Comme son adjectif l'indique, elle est une conséquence (malheureuse) de la poussée, et non une cause.
Car pour une poussée donnée sur les pales de l'hélice, plus la vitesse induite sera faible, plus les pertes d'énergie cinétique emportée dans ce flux induit seront réduites. Ainsi, moins de puissance sera à fournir sur l'arbre.
Pour vous en convaincre pensez à l'effet de sol qui, diminuant cette vitesse induite, diminue aussi très notablement la puissance nécessaire au vol stationnaire.

[Nekama]

Bonjour,

C'est bien la vitesse induite, oui. Et elle est bien une conséquence de la rotation du rotor. Je ne dirais pas qu'elle est une conséquence de la poussée mais la cause (ou en tout cas simultanée : par conservation de la qtt de mvt, le déplacement d'air vers le bas s'accompagne d'une poussée du rotor vers le haut).

Le raisonnement n'est pas de moi... Le voici dans Leishman p.63 et on le trouve dans tous les ouvrages sur les hélico's.
Ce qui est de moi, c'est d'essayer de l'appliquer à un carénage et je me focalise sur T/P.

...

Pièce jointe 436352

[harmoniciste]

Les pales s'appuient sur l'air pour développer leur portance. En conséquence cet air est accéléré vers le bas. Les théories doivent donc tenir compte de ce fait (en particulier celle de Froude) pour prévoir la puissance nécessaire au vol.
En négligeant les pertes par friction de l'air sur les pales on a P_uissance = T_raction* V_induite
Pour T donnée, plus Vi est faible, moins il faut de puissance

[Nekama]

Oui. Je suis d'accord.

J'ai noté Vo pour V_ind

Mais on a aussi que T = m'.W = ( rho.A.Vo ) W

Pour T donné, si W augmente, Vo diminue.

Et justement si la veine se resserre, W augmente (conservation du débit)

Donc Vo diminue et P diminue pour T constant si la veine reserre.

[Nekama]

For the record :

L'erreur vient de la seconde équation.

P = T.Vo = rho.A.Vo^3 / a (2)

T représente ici la poussée totale mais c'est seulement la poussée du rotor qu'il faut prend en compte.

Mais T a 2 sources :
- le rotor
- le carénage (qui peut fournir un T > 0 ou < 0 )

P = (T - T_D) . Vo

Et la conclusion finale était fausse.

La carénage doit élargir la veine pour augmenter le rapport T/P, comme indiqué dans Leishman (et les ouvrages qui traitent du sujet).