
- Forum
- Futura-Sciences : les forums de la science
- MATIERE
- Physique
- Comment le prof est passé de cette formule a une autre
Comment le prof est passé de cette formule a une autre
- 06/04/2021, 12h41 #1invite4c0d74f9
- Date d'inscription
- janvier 1970
- Messages
- 5
 Comment le prof est passé de cette formule a une autre
Comment le prof est passé de cette formule a une autre
------
Dernière modification par albanxiii ; 06/04/2021 à 21h17. Motif: titre, évitez de confondre être et avoir !

- 06/04/2021, 12h45 #2Deedee81
- Date d'inscription
- octobre 2007
- Localisation
- Courcelles - Belgique
- Âge
- 63
- Messages
- 47 509
Re : Comment le prof a passé de cette formule a une autre
Salut,
Que signifie "Pe" ?"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
- 06/04/2021, 12h52 #3obi76
- Date d'inscription
- mai 2007
- Localisation
- Normandie
- Âge
- 41
- Messages
- 17 669
Re : Comment le prof a passé de cette formule a une autre
Dernière modification par obi76 ; 06/04/2021 à 13h04.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 06/04/2021, 14h01 #4invite4c0d74f9
- Date d'inscription
- janvier 1970
- Messages
- 5
Re : Comment le prof a passé de cette formule a une autre
phi : potentiel de vitesse ; psi : fonction de courant ; Pe: nombre sans dimension , qui caractérise l’importance relative de la conduction et de la convection

- Aujourd'huiA voir en vidéo sur Futura
- 06/04/2021, 14h10 #5gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Comment le prof a passé de cette formule a une autre
On a l'impression que dans la première équation, la partie droite est vectorielle avec des
 et
et  et que Pe est un scalaire, alors que le second membre est scalaire.
et que Pe est un scalaire, alors que le second membre est scalaire.
C'est quoi ? (pas le
? (pas le  )
)
Si ce n'est pas le cas que désigne et
et 
Un énoncé plus détaillé serait bienvenu pour qu'on puisse répondre.
- 06/04/2021, 14h12 #6obi76
- Date d'inscription
- mai 2007
- Localisation
- Normandie
- Âge
- 41
- Messages
- 17 669
Re : Comment le prof a passé de cette formule a une autre
Ha c'est de la méca flu ??
Fallait deviner...\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 06/04/2021, 14h36 #7Deedee81
- Date d'inscription
- octobre 2007
- Localisation
- Courcelles - Belgique
- Âge
- 63
- Messages
- 47 509
Re : Comment le prof a passé de cette formule a une autre
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
- 06/04/2021, 16h15 #8obi76
- Date d'inscription
- mai 2007
- Localisation
- Normandie
- Âge
- 41
- Messages
- 17 669
Re : Comment le prof a passé de cette formule a une autre
Ben là on est toujours dans le flou le plus complet. pe en général c'est le nombre de Peclet : https://fr.wikipedia.org/wiki/Nombre_de_P%C3%A9clet
Or je ne vois pas où il s'agit de température ici.
Bref, sans un énoncé un poil plus clair, on parle dans le vide.\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 06/04/2021, 16h52 #9invite4c0d74f9
- Date d'inscription
- janvier 1970
- Messages
- 5
Re : Comment le prof a passé de cette formule a une autre
Ces nouvelles variables qui sont habituellement nommées «coordonnées des lignes de courant», ont été introduites pour la première fois par Boussinesq en mécanique des fluides dans l’analyse des écoulements à grand nombre de Reynolds.
ce symbole désigne la température adimensionnelle .
désigne la température adimensionnelle .

- 06/04/2021, 16h58 #10obi76
- Date d'inscription
- mai 2007
- Localisation
- Normandie
- Âge
- 41
- Messages
- 17 669
Re : Comment le prof a passé de cette formule a une autre
Merci, mais comment voulez-vous qu'on le devine ?Ces nouvelles variables qui sont habituellement nommées «coordonnées des lignes de courant», ont été introduites pour la première fois par Boussinesq en mécanique des fluides dans l’analyse des écoulements à grand nombre de Reynolds.
ce symbole Pièce jointe 436485 désigne la température adimensionnelle .
A défaut d'avoir un tantinet plus d'éléments sur la question initiale, vous n'aurez pas de réponse : on n'a AUCUNE idée du contexte. On ne va pas l'inventer. Il aura déjà fallu 4 messages pour savoir qu'on parle de mécanique des fluides, 9 messages pour comprendre qu'il y a la température dans la première formule, que Pe c'est Peclet.... Bref on ne va pas passer la journée à essayer de deviner ce que vous demandez.\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 06/04/2021, 17h10 #11gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Comment le prof a passé de cette formule a une autre
Et vous n'avez pas répondu sur le caractère vectoriel ou non.
On a l'impression que dans la première équation, il y a le gradient de température à gauche et le Laplacien de la température adimensionnée à droite.
Il faut expliciter.
- 06/04/2021, 18h54 #12Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Comment le prof a passé de cette formule a une autre
Pourquoi ne pas demander directement au prof ?
Sans questions il n'y a que des problèmes sans réponses.
- 06/04/2021, 18h55 #13invite4c0d74f9
- Date d'inscription
- janvier 1970
- Messages
- 5
Re : Comment le prof a passé de cette formule a une autre
l y a le gradient de température à gauche et le Laplacien de la température adimensionnée à droite
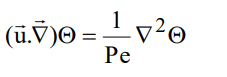

- 06/04/2021, 18h56 #14obi76
- Date d'inscription
- mai 2007
- Localisation
- Normandie
- Âge
- 41
- Messages
- 17 669
Re : Comment le prof a passé de cette formule a une autre
Donc déjà, première déduction : il s'agit d'un état stationnaire. 14 messages qu'on aurait pu éviter si on avait eu un minimum d'éléments de la part du primo-posteur...
Dans 30 messages on va peut-être apprendre qu'il est incompressible, aussi...
Vais ouvrir ma roulotte, moi...Dernière modification par obi76 ; 06/04/2021 à 19h15.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 06/04/2021, 19h34 #15invite4c0d74f9
- Date d'inscription
- janvier 1970
- Messages
- 5
Re : Comment le prof a passé de cette formule a une autre
je vais clarifier les choses pour qu'elless soient évidentes . ( on travaille en utilisant les coordonnées cylindriques)
5.png
et 6.png
psi : la fonction de courant , voir la deuxième photo
phi : le potentiel de vitesse , voir la première photo.
le but est comment de passer de coordonnees cylindriques ( r, theta )à coordoonnees de bousinesq ( psi , phi )
- 06/04/2021, 19h42 #16gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Comment le prof a passé de cette formule a une autre
Ce n'était pas ce qui était écrit dans le premier message !l y a le gradient de température à gauche et le Laplacien de la température adimensionnée à droite
Pièce jointe 436493
Discussions similaires
-
Comment compter les H dans cette formule de triglycérides ?
Par invite6726c303 dans le forum ChimieRéponses: 2Dernier message: 30/09/2018, 19h00 -
Comment lit-on cette formule ?
Par Meiosis dans le forum Mathématiques du supérieurRéponses: 13Dernier message: 07/02/2018, 23h25 -
Comment trouver formule NRJ cinetique et autre du meme genre
Par invite40f82214 dans le forum PhysiqueRéponses: 9Dernier message: 26/12/2007, 20h47 -
prof après une autre carrière
Par invite4021e8ad dans le forum Orientation après le BACRéponses: 0Dernier message: 05/07/2007, 00h11 -
comment on passe de la basique formule pour calculer une concentration molaire C=n/V
Par invite3ef66143 dans le forum ChimieRéponses: 4Dernier message: 31/10/2005, 18h11
Fuseau horaire GMT +1. Il est actuellement 15h31.


 (ou à n'importe qui arrivant à comprendre).
(ou à n'importe qui arrivant à comprendre).