Comment lit-on cette formule ?

[Meiosis]

Bonjour,

J'essaye depuis plusieurs heures de calculer cette formule (en pièce jointe), ne serait-ce que pour n=1 mais je n'y parviens pas, pouvez-vous me dire comment ça se calcule ?

Merci à vous.


-----

[azizovsky]

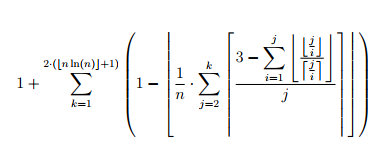
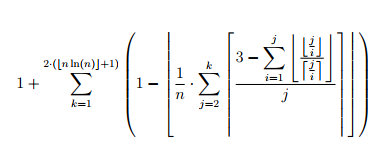
Bonjour, pour les symboles, regarde ici : https://fr.wikipedia.org/wiki/Partie..._fractionnaire

[minushabens]

pouvez-vous me dire comment ça se calcule ?

tu cherches quoi au juste? un équivalent quand n tend vers l'infini?

[jacknicklaus]

le résultat est jamais bien loin de 2n.Ln(n)

[A voir en vidéo sur Futura]

[Meiosis]

Bonjour, pour les symboles, regarde ici : https://fr.wikipedia.org/wiki/Partie..._fractionnaire

En fait ce que je ne comprends pas ce sont les sommations. J'ai bien compris les arrondis par excès et par défaut.

tu cherches quoi au juste? un équivalent quand n tend vers l'infini?

Avoir un exemple avec n=1 pour savoir comment ça se calcule.
Après je saurai le faire avec le reste.

[gg0]

Comme toujours, avec des symboles emboités, il faut partir de l'intérieur pour comprendre, mais comme il y a des sommes, on est obligé de prendre le temps d'exécuter ces sommes : donc pour n=1, la somme qui suit le 1 va de 1 à 2 pour k; on prend k = 1 puis on a 1 moins une partie entière à traiter. C'est la partie entière d'une expression qui est une somme (1/n=1) pour j variant de 2 à k, donc une somme vide, ça fait 0. On reprend à k=2, et on se retrouve avec une somme pour j variant de 2 à 2, un seul terme que tu peux écrire facilement et décoder.

A noter : Cette expression est mal écrite, car la valeur k=1 donne toujours une somme vide.

Cordialement.

[Meiosis]

Merci.

Je ne suis pas certain du tout : on obtiendrait donc 1 pour cette expression pour n=1 ?

[jacknicklaus]

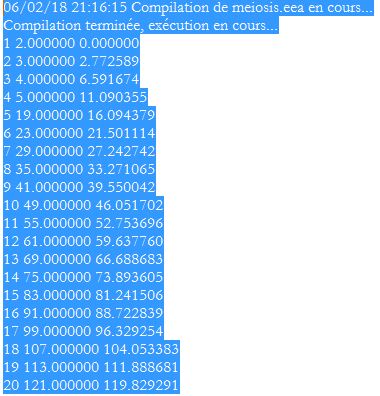
Les 3 nombres sont : n, le résultat de ta formule, et 2.n.Ln(n)
sauf erreur...

[Meiosis]

Merci pour cette réponse.

[Meiosis]

Juste une petite question : tu aurais la formule que tu as entré sur excel (je pense) ? Merci.

[jacknicklaus]

Non, pas Excel. C'est un petit script dans un langage proche du C. je pense que si tu connais le C tu le liras sans difficulté. le seul truc à savoir est que % est une balise de début ou fin de définition de fonction

%Plancher(x)
%return(Flottant(Entier(x)))

%Plafond(x)
%Return(Flottant(Entier(x+1)))

%f(j)
k = 0.0
kj = Flottant(j)
for(i=1;i<=j;i+=1)
ki = Flottant(i)
k += Plancher(kj/ki)/Plafond(kj/ki)
endfor
%return((3 -k)/kj)

%g(k,n)
s = 0.0
for(j=2;j<=k;j+=1)
s += Plafond(f(j))
endfor
%return(1-Plancher(s/n))

%h(n)
r = 0.0
for(k=1; k<=(Plancher(n*Log(n))+1)*2;k+=1)
r += g(k,n)
endfor
%return(1+r)
//
for(n=1;n<=20;n+=1)
Message("%z %z %z",n,h(n),2*n*Log(n))
endfor

[Médiat]

%Plafond(x)
%Return(Flottant(Entier(x+1)))

Donc le plafond(2) = 3 ...

[jacknicklaus]

Donc le plafond(2) = 3 ...

damned !

oh le vilain bug débusqué !

[Meiosis]

En effet ce n'est pas excel, je me suis mal exprimé, je voulais juste savoir s'il y avait un moyen de la rentrer sous excel. Je pense que oui.

Sinon merci pour ce programme, je vais le regarder de plus près.