Pendule simple

[Anduriel]

Bonjour,

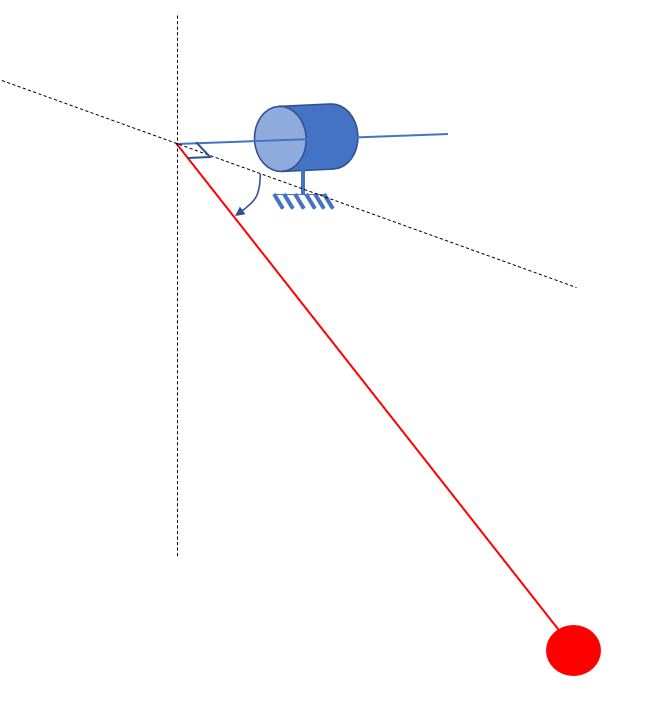
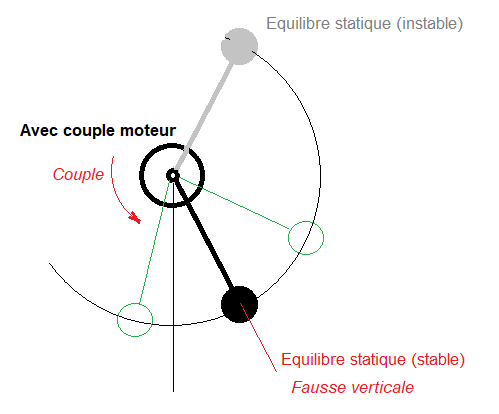
Je considère un pendule simple avec une masse M au bout d'un fil de longueur l et tournant autour d'un point O (fixe) qui représente un axe moteur tournant.
Je néglige tout frottement.
1) L'équation du pendule simple me donne: d²(theta)/dt² = -g/l*sin(theta)
2) L'équation du moteur donne: J*d²(theta)/dt² = Couple appliqué
3) Or le couple, à chaque instant, vaut C = Mlg*cos(theta).

En mettant 1) dans 2) j'ai J*(-gsin(theta)/l) = Mlg*cos(theta) soit M = -J/l²*tan(theta)

Ca me semble complètement grotesque et sans aucun sens (J, M, l constant, mais pas theta)... où est l'erreur?
Merci
-----

[gts2]

Bonjour,

On a du mal à comprendre : vous prenez deux problèmes différents :
1- un pendule soumis uniquement à la gravité
2- un moteur

Pourquoi voulez-vous qu'il y ait un rapport entre les deux (3) ?

[Anduriel]

Bonjour,

Le pendule est attaché à l'axe moteur, qui l'entraîne donc en rotation. Il y a 2 systèmes reliés par le fil du pendule.

[gts2]

Avec un schéma cela serait plus simple, mais on peut essayer : je suppose l'axe du moteur horizontal, axe sur lequel coulisse le fil (de manière à ce qu'il n'y ait pas d'enroulement) ; dans ce cas les deux sont différents, l'un représente l'angle du fil, l'autre l'angle de rotation de l'axe sans lien entre eux.

[A voir en vidéo sur Futura]

[Sethy]

Je pense qu'il s'agit d'un pendule à la mode du "Professeur Tournesol" avec un axe vertical.

Même si j'ai bien compris le problème, je rejoins gts2 sur le fond : les 2 theta n'ont rien à voir entre eux. Il vaudrait mieux utiliser deux notations différentes (theta et phi par exemple).

[Anduriel]

Bonjour,

Voici un schéma. Pour moi les angles sont les mêmes puisque la liaison est rigide entre les 2 systèmes (rouge: pendule, bleu: axe moteur).

[coussin]

Il vous faut une équation différentielle faisant intervenir thêta. Dans votre message #1, vous avez fait disparaître thêta’’ donc il ne reste plus grand chose de dynamique
L'équation sera thêta’’ = -g/l*sin(theta) + (le terme dû au moteur que je ne connais pas) et c'est cette equa diff qu'il faut résoudre.

[gts2]

Si la liaison est rigide, ce n'est pas un fil donc ce n'est plus un pendule simple.

Et donc il y a deux moments qui s'exercent sur la tige : le moment du moteur et le moment du poids.
Donc l'équation (1) est inexacte et l'équation (2) est rigoureusement (après correction) la même que l'équation (1)

[Black Jack 2]

Bonjour,

Pas clair.

Si le moteur tourne à vitesse de rotation w constante, alors theta = w * t

Si le moteur fournit un couple constant ... alors il faut le préciser.

Ou alors, doit-on trouver la valeur du couple moteur nécessaire en fonction de theta pour conserver une vitesse constante ?

Ou quoi d'autre ?

Quelle est l'équation différentielle demandée (quoi en fonction de quoi) ?

[Anduriel]

En fait, oublions que c'est un moteur ça sera plus simple.
Le schéma représente juste un axe en rotation (dans le pivot) entrainé par la masse (en rouge), via le coude à 90°.
Il n'y a aucun frottement/résistance de l'axe dans ce pivot.

Le couple au niveau du pivot, induit par la masse, vaut C = mglcos(theta).
Mais quelle est l'équation différentielle régissant le mouvement du "pendule"?
Pour moi il s'agit des équations du pendule simple (après tout, sur la masse s'appliquent simplement la tension du "fil" et le poids de la masse, puisqu'on néglige tout effort au niveau du pivot).

Edit: peut-être que tout simplement mon incompréhension vient du fait que le système global est rigide donc il n'y a pas de tension du fil.
Si j'applique le PFD au niveau de l'axe dans le pivot (d'inertie J), j'ai tout simplement: Jd²theta/dt² = mglcos(theta).
Si oui, connaissez-vous une méthode de résolution ?

[gts2]

Donc vous tombez bien sur l'équation du pendule simple après avoir supprimé le moteur.

Il n'y a pas de solution analytique à cette équation.

[Anduriel]

Je ne retombe pas dessus puisque l'équation du pendule vaut d²theta/dt² = -gsin(theta)/l

[gts2]

Vous avez changé la signification de \theta : usuellement c'est l'angle par rapport à la verticale, vous l'avez pris par rapport à l'horizontale.

[Anduriel]

J'ai realisé après 13 messages que j'avais mal pris ma référence de theta sur le pendule... Merci !

[le_STI]

Salut

Il n'y a aucun frottement/résistance de l'axe dans ce pivot.

Le couple au niveau du pivot, induit par la masse, vaut C = mglcos(theta).

S'il n'y a ni moteur ni frottement dans la liaison pivot, pourquoi introduis-tu un couple hypothétique?

Comme l'ont dit d'autres, il faut distinguer le cas "pendule simple" et le cas "masse entrainée par un moteur".

[le_STI]

A vrai dire tu cites 3 situations différentes :

1) L'équation du pendule simple me donne: d²(theta)/dt² = -g/l*sin(theta)
2) L'équation du moteur donne: J*d²(theta)/dt² = Couple appliqué
3) Or le couple, à chaque instant, vaut C = Mlg*cos(theta).

1. Pendule simple, on ne peut pas introduire de couple moteur
2. Equation uniquement utile dans le cas où on a à faire à un mouvement accéléré
3. Equation régissant le couple moteur dans le cas où la vitesse est constante

Il est donc logique que tu ne parviennes pas à concilier les trois...

[harmoniciste]

Il n'y a pas de solution analytique à cette équation.

Bonjour,
Je subodore quand-même que pour de petits angles, de position d'équilibre statique dû au couple, et de position initiale (par rapport à la verticale), la solution reste très proche de celle du pendule simple en remplaçant la verticale par la position d'équilibre statique stable
Rien ne va plus, évidemment, si l'angle maximum de l'oscillation par rapport à la verticale s'approche trop de la position d'équilibre statique instable (car alors le mouvement alternatif n'aurait plus rien de sinusoïdal et sa période tendrait vers l'infini (équilibre en ce point)