
- Forum
- Futura-Sciences : les forums de la science
- MATIERE
- Physique
- Biprisme de Fresnel :
Biprisme de Fresnel :
- 13/10/2022, 15h18 #1lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Biprisme de Fresnel :
------

- 13/10/2022, 15h27 #2gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Le schéma a) vous donne le schéma de Young équivalent (les deux sources S1 et S2)

- 13/10/2022, 15h32 #3lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
Merci.
Néanmoins, je vois pas comment continuer le calcul, il y a bien une symétrie entre S1 et S2 mais ça ne m'aide pas...
Par ailleurs il y a cette égalité que je ne parviens pas à comprendre ...
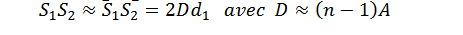
Dernière modification par lesurveilleur ; 13/10/2022 à 15h36.

- 13/10/2022, 15h37 #4gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Pour Young on a delta= ax/D
Quel est l'équivalent de D ?
Quel est l'équivalent de a ?
En notant O le sommet du prisme, dans le triangle S1SO, quel est l'angle S1OS ?
- Aujourd'huiA voir en vidéo sur Futura
- 13/10/2022, 15h41 #5lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
a=S1S2/2
D=l+d
S1S2/d=tan(alpha)
On trouve : S1S2=(d * alpha * x)/2D
Ce n'est pas se que je dois trouver
Dernière modification par lesurveilleur ; 13/10/2022 à 15h43.

- 13/10/2022, 16h06 #6gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
C'est presque cela : pourquoi /2 dans a=S1S2/2 ? que représente alpha ?
J'ai du mal à voir un rapport entre vos expressions initiales et celle-ci.
En prenant vos expressions, je trouve S1S2=d tan(alpha)=2a qui est presque exact aux problèmes soulevés près.
Vous reportez après correction dans ax/D et vous devez trouver la bonne expression.
- 13/10/2022, 16h18 #7lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
Résumons :
D=A(n-1)=l+d
S1S2=2a
i=ax/D
J'essaye de trouver i :
i = (S1S2/2) * x / (A(n-1))
Cela me donne pas se qu'il faut...
- 13/10/2022, 16h27 #8gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Le D de la formule d'Young est la distance entre les sources et l'écran ; D=l+d OK
Alors que D=A(n-1) est l'angle de déviation, à ne pas confondre !
Je en vois toujours pas d'où vous sortez le 2.
erreur précédente A(n-1) est un angle, D vaut l+d.
Il faut maintenant calculer S1S2
- 13/10/2022, 16h32 #9lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
J'ai :
i=S1S2 * x/ (l+d)
Je dois maintenant faire apparaître l'angle A(n-1) :
Je suis pas sur mais je dirais :
A(n-1)=l/M(y)=tan (alpha) ; M(y) le point sur l'écran...Dernière modification par lesurveilleur ; 13/10/2022 à 16h35.

- 13/10/2022, 16h35 #10gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Qu'appelez-vous M(y) et alpha ?

- 13/10/2022, 16h38 #11lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
M(y) le point sur l'écran,
alpha=D celui de la figure j'ai changé le nom car ça porte à confusion...
- 13/10/2022, 16h41 #12gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Le point de l'écran est déjà pris en compte : c'est le x.
En notant O le sommet du prisme, dans le triangle S1S2O, quel est l'angle S1OS2 ?
En déduire S1S2=a
- 13/10/2022, 16h43 #13lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
On a S1S**2+d**2=S1O**2
On en déduis que S1S2=a
Comment injecter A(n-1) ?Dernière modification par lesurveilleur ; 13/10/2022 à 16h47.

- 13/10/2022, 16h49 #14gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Je répète :
"En notant O le sommet du prisme, dans le triangle S1S2O, quel est l'angle S1OS2 ?"
- 13/10/2022, 16h51 #15lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
tan(D)=S1S/d En négligeant la déviation du prisme...

- 13/10/2022, 16h55 #16gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Si on néglige la déviation du prisme S1S2=0 !
L'angle vaut bien S1S2/d et que vaut cet angle en fonction de la déviation du prisme alpha=A(n-1)
- 13/10/2022, 16h59 #17lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
d*A(n-1)=d*D=S1S2
Par ailleurs tan(D)=x/lDernière modification par lesurveilleur ; 13/10/2022 à 17h04.

- 13/10/2022, 17h08 #18gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
On y est presque : l'angle vaut 2D=2A(n-1) (voir le dessin)

- 13/10/2022, 17h10 #19lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
2A(n-1)=2dx/l ?

- 13/10/2022, 17h13 #20gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664

- 13/10/2022, 17h17 #21lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
Donc, d*A(n-1)=2D (1)
Or, ax/(l+d)=delta (2)
On injecte (2) dans (1) grâce à d
- 13/10/2022, 17h32 #22lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
Je corrige mon anergie :
d*A(n-1)=2*D* d= S1S2
Or, ax/(l+d)=delta
Ici a=S1S2
(S1S2) * x/(l+d)= delta
Donc,
2*D* d * x/(l+d)= delta
- 13/10/2022, 17h38 #23gts2
- Date d'inscription
- janvier 2018
- Localisation
- Touraine
- Messages
- 13 664
Re : Biprisme de Fresnel :
Aux fautes de frappe près OK.
d*2*A(n-1)=S1S2
- 13/10/2022, 17h40 #24lesurveilleur
- Date d'inscription
- septembre 2022
- Âge
- 30
- Messages
- 146
Re : Biprisme de Fresnel :
merci beaucoup j'ai enfin compris...
Merci pour ta patience

« Variation de l'enthalpie négative ou enthalpie négative?
|
Temple maya de Tikal.. au look de haut-parleur anti-sismique ? »
Discussions similaires
-
Probleme de comprehension concernant le Biprisme de Fresnel
Par invite22415ee4 dans le forum PhysiqueRéponses: 1Dernier message: 27/05/2021, 07h38 -
Fresnel
Par invite1dc24275 dans le forum PhysiqueRéponses: 2Dernier message: 31/10/2018, 09h08 -
Transformée de fourier / biprisme de Fresnel
Par invite814a7e57 dans le forum PhysiqueRéponses: 1Dernier message: 26/02/2016, 16h37 -
problème de compréhension biprisme de fresnel
Par Minialoe67 dans le forum PhysiqueRéponses: 9Dernier message: 06/01/2014, 20h22 -
Biprisme Fresnel
Par invite1d656ca6 dans le forum PhysiqueRéponses: 2Dernier message: 13/01/2007, 21h09
Fuseau horaire GMT +1. Il est actuellement 06h47.

