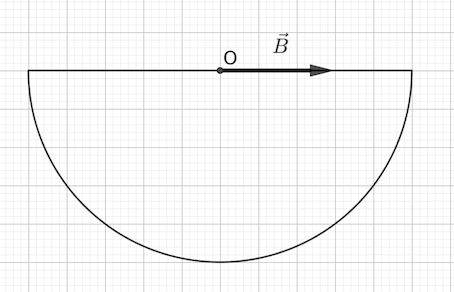
Bonsoir j'ai un exercice dans le quel on me demande de trouver le champ magnétique en un point de l'axe de révolution d'un demi-cylindre parcourus par un courant en analysant les symétrie et les invariance je sais que le champ est perpendiculaire à l'axe mais à partir de là je suis bloqué . Aidé moi s'il vous plaît
Bonjour,
J'ai bien peur qu'on ne puisse aller plus loin avec uniquement les symétries.
Champ perpendiculaire à l'axe est exact, mais il faudrait être plus précis.
Je pense que le champ est porté par u(tétâ) mais sa s'arrête là,je voudrais savoir comment trouver le champ sur l'axe
u theta n'a pas de sens sur l'axe (il n'est pas défini).
Il reste maintenant à intégrer Biot et Savart en ne prenant que l'intégrale utile.
Merci mais pouvez vous être un peu plus clair
u theta est défini comment étant perpendiculaire à OM, si vous êtes en O, perpendiculaire à OO n'est pas défini.
B est parallèle au plan du demi-cylindre
Pour ce qui est de Biot et Savart, on découpe le cylindre en fil de section dS (à prendre en coordonnées cylindriques), ce champ est connu, on projette sur la direction utile et on intègre.
Donc si je comprends le champ est porté par (0z)
Mais le champ créé par un fil élémentaire est porté par u (theta). dB=(Uo*dI)/(2π×r)
C'est ce vecteurs que je dois projeté sur oz?
Dernière modification par GFC03 ; 22/03/2023 à 14h48. Motif: Incomplet
Tout dépend ce que vous appelez z ...
Un dessin pour être sûr :
Votre champ élémentaire est correct, il reste à le projeter et intégrer.
Merci en prenant compte de tout ça j'ai exprimé u(theta) en fonction de ox et oy mon champ final est donc. B=-((UoJsR)/π)j(vecteur)
Est ce correct ?
Dernière modification par GFC03 ; 22/03/2023 à 19h33. Motif: Incomplet
Cela m'a l'air correct.
Merci
