Diable/chariot à 3roues ( dit à escalier) ... Comment ça marche ?

[sh42]

Bonjour,

J'ai essayé de mettre en équation le système à 3 roues mais c'est trop fort pour mes compétences.
Cependant une comparaison chiffrée des deux systèmes doit être réalisable.
Je mets ce que j'ai fait.

Calcul des forces
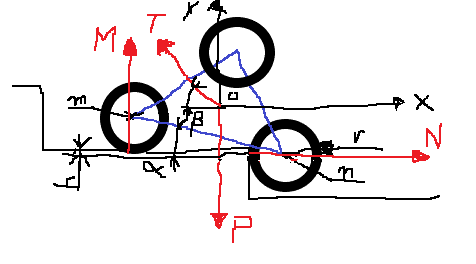
Calculons le moment de M par rapport au point o*:
MM = - M *om * cos (30° - α)

Calculons le moment de N par rapport au point o*:
MN = N * on * sin ( 30° + α )

Les moments de P et de T sont MP = 0, MT = 0 car elles passent par le point o.

Comme la somme des moments = 0, nous avons*:
[ - M * om * cos (30° - α) ]+ [ N * on * sin ( 30° + α) ] = 0
donc*: M * om * cos (30° - α) = N * on * sin ( 30° + α)
comme om =on du fait de la construction, nous avons M * cos (30°- α) = N * sin (30° + α),
donc nous avons N = ( M * cos (30°- α) ) / ( sin (30° + α))
sin α = ( r + h ) / l , si H est la hauteur de la marche
α varie de α = arc sin [(r + H ) / l] à α = 0, r étant le rayon des roues.

Projetons les forces sur ox et oy
sur ox N-T cosβ = 0, soit en remplaçant N, ( M * cos (30°- α) ) / ( sin (30° + α)) – T cosβ = 0
sur oy -P + M + T sinβ = 0,
-----

[mécano41]

Bonjour à tous,

Je remonte ce sujet car il m'a donné l'idée de m'amuser...

C'est pour EXCEL uniquement (à cause du VBA). Il faut valider les macros à l'ouverture.

Nota 1 :

- comme indiqué, le calcul d'efforts ne tient pas compte des frottements de roulement des roues ni de ceux de leurs axes de rotation
- le cycle est la montée d'une marche ; il y a plusieurs phases
- les données principales sont à mettre dans les cellules jaunes (voir nota2)
- l'inclinaison est donnée par un curseur (voir nota 2)
- la position, dans la montée, sur une trajectoire parallèle aux marches, est donnée par un curseur

Nota 2 :

- après ces opérations, il y a un temps de réponse car il y a des calculs pour le graphique d'effort sont faits selon une méthode qui n'est pas rapide

Tous les éléments sont dans les diverses feuilles...

Cordialement

[sh42]

Bonsoir,

Beau travail mécano41. Cela va permettre à marzan de voir quel sera le meilleur compromis pour son besoin, ( voir #8).

Cependant du fait du transport qu'il a à faire, ( un moteur hors-bord), qui a toute la masse " en tête ", la position des roues ne devra pas être à la position d'un diable classique mais plus sous le centre de gravité du moteur.

marzan se posait aussi la question si le diable classique n'était pas plus avantageux que le diable à 3 roues.

[mécano41]

Bonjour,

Pour le CdG de la charge, il suffit de changer sa position dans les cellules correspondantes de l'appli...(toutes les cellules jaunes sont modifiables). Il faut vérifier que la charge et la nacelle ne touchent pas les nez de marches...

J'ai oublié de dire :

- l'appli. est limitée à des marches ayant des proportions proches du standard. En dehors de cela, soit il y a disparition du dessin, soit on ne représente pas la totalité du mouvement
- l'appli. part du principe que les roues ne franchissent jamais le nez de marche en s'appuyant dessus comme lorsqu'il y a une seule roue. C'est l'appui d'une roue sur une marche et la contremarche qui fait basculer le croisillon pour amener une autre roue au contact du dessus de la marche suivante
- l'appli. ne traite pas non plus du cas des marches sans contremarche

... on ne peut pas tout faire

Cordialement

[sh42]

Bonjour,

J'ai utilisé un diable à 3 roues dans un escalier sans contremarches. C'est galère, car c'est le croisillon qui prend appui sur le nez de marche et qui fait basculer le croisillon. En plus le diable doit reculer pour permettre à la roue la plus basse de " passer " le nez de marche.

les roues ne franchissent jamais le nez de marche en s'appuyant dessus comme lorsqu'il y a une seule roue

Ca, ce ne doit pas être toujours appliqué dans la vie courante car il faut une certaine adéquation entre le diamètre des roues, la distance entre les axes des roues, la hauteur des marches et le giron.