Bonjour,
Dans cette image:
angle.jpg
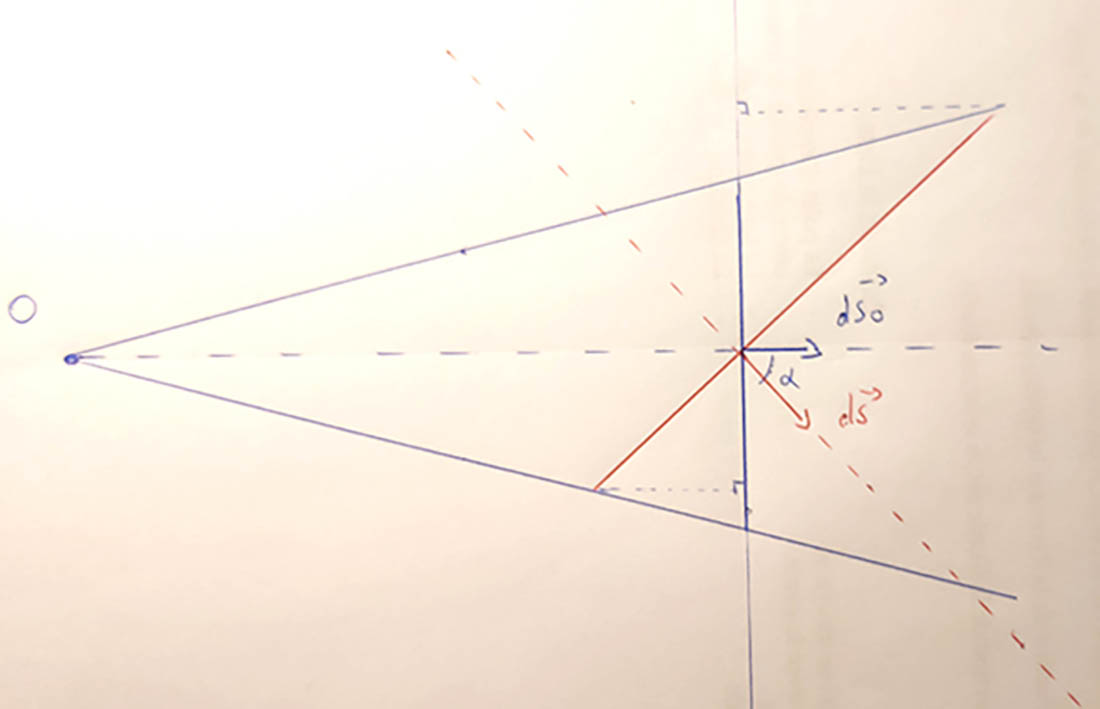
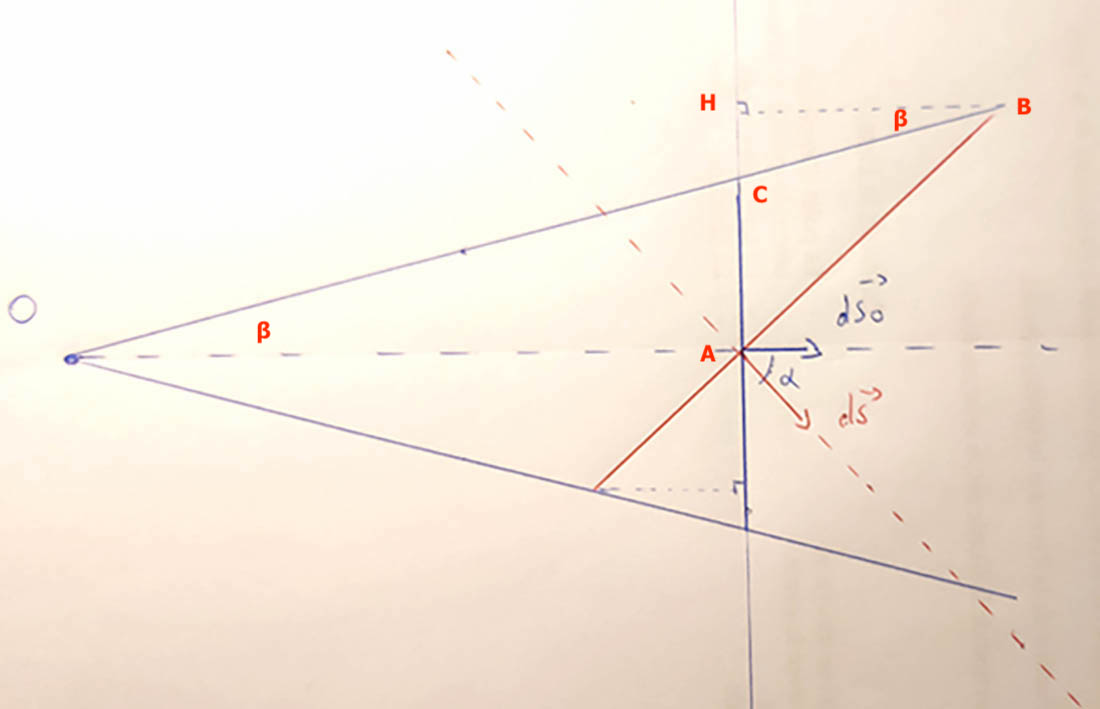
On a donc une surface élémentaire dS qui a pour surface apparente, vu du point O, égale à dS.cos(alpha). Du coup l'angle solide est dOmega = dS.cos(alpha)/R²
Juste pour avoir confirmation. La surface apparente est approximativement dS cos(alpha). Je voudrais avoir la confirmation que ce n'est pas une égalité stricte mais bien une approximation qui dépend de R et alpha ?
Merci
Out! Out! You, Demons Of Stupidity!!
Bonjour,
On est bien d'accord que dΩ est la différentielle de Ω ?
Si oui, c'est bien une égalité.
Par contre Ω = S.cos(α)/R² est bien une approximation
dΩ est l'angle solide élémentaire donc oui la différentielle à priori.Envoyé par gts2
Mais le vecteur0 =
le produit scalaire, c'est à dire que par définition le projeté de la surface élémentaire pour obtenir la surface élémentaire apparente.
Voir mon dessin:
donc je ne comprends pas pourquoi c'est une égalité ?? On voit sur mon dessin que le projeté ne correspond pas à la surface élémentaire apparente. Pourtant le produit scalaire correspond à cela.
Merci
Dernière modification par mamono666 ; 15/08/2023 à 00h04.
Out! Out! You, Demons Of Stupidity!!
HC est l'écart entre la projection et la surface apparente
HB=AB sin(α) ; HC=HB tan(β)=AB sin(α)tan(β) avec AB et β infiniment petit d'ordre 1, donc la correction à appliquer est d'ordre 2 (peut-être moins parce q'il y excès en haut et défaut en bas)
Donc par passage à la limite, cela disparait bien.
Si on cherche la petite bête, S est la surface de la calotte sphérique, cela fait une autre "erreur" qui disparait elle aussi.
Ok donc c'est bien une approximation.
Merci pour les précisions.
Out! Out! You, Demons Of Stupidity!!
Non, ce n'est pas une approximation, la différentielle est l'application linéaire tangente, donc par définition, il n'y a pas de termes d'ordre deux.
