Bonsoir a tous ! Comme indique dans le titre j'ai un petit probleme de contrainte concernant l'optimisation d'une fonction, cette fonction représente l’évolution de l’énergie dégagée par 3 aimants qui flottent dans un bassine circulaire remplie d'eau, leur position d’équilibre est un triangle équilatérale (ils se repoussent simultanément), cette position est stable.
Le but est de trouver cette position d’équilibre en utilisant la fonction fmincon, comme on a trois aimants, on a 3 points a trouves et donc 6 coordonnées (x1,x2,x3,y1,y2,y3).
Mes contraintes décrivent l’équation d'un cercle (la bassine).

Fonction :

Code:
[ Energie ] = W(X)

 on note ici y1 = x4 , y2=x5 , y3=x6

R12=sqrt((X(1)-X(2)).^2+(X(4)-X(5)).^2);
R23=sqrt((X(2)-X(3)).^2+(X(5)-X(6)).^2);
R13=sqrt((X(1)-X(3)).^2+(X(4)-X(6)).^2);

Energie=1/R12 + 1/R13 + 1/R23;
et les contraintes non linéaires (c est la contrainte d’inégalité, ceq la contrainte d’inégalité)

Code:
[c,ceq]=constraint(X)

% C(X) <= 0
% Ceq(X) = 0

c = [] ;
    
ceq = [X(1).^2 + X(4).^2 -1 ; X(2).^2 + X(5).^2 -1 ; X(3).^2 + X(6).^2 -1];
Voici le code pour optimiser la fonction :

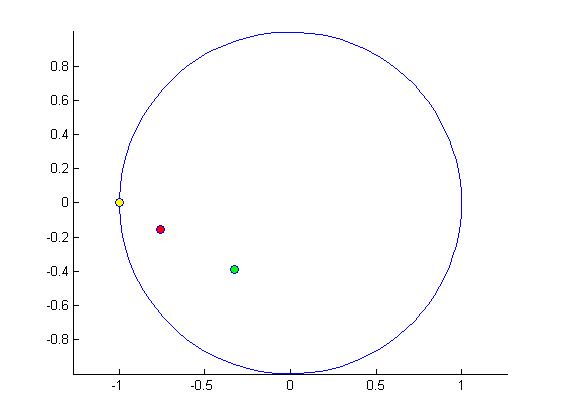
Code:
n=3;  %nombres d'aimants

% Position Initiale


X0=[0.1;0.2;0.3;0.1;0.2;0.3];

% Minimisation

LB = [-1;-1;-1;-1;-1;-1];
UB = [1;1;1;1;1;1];

opts = optimset('Display','iter','Algorithm','interior-point', 'MaxIter', 100000000, 'MaxFunEvals',100000000);


[X,fval]=fmincon(@W,X0,[],[],[],[],LB,UB,@constraint,opts);

%coordonnees des aimants

A1=[X(1);X(4)]
A2=[X(2);X(5)]
A3=[X(3);X(6)]

X(1)=-1;

X(4)=0;
J'ai aussi fixe la position de l'aimant 1 pour avoir moins de calcul cependant matlab semble bloque et il me donne donc ca au final :

Code:
No feasible solution found.

fmincon stopped because the size of the current step is less than
the default value of the step size tolerance but constraints are not
satisfied to within the default value of the constraint tolerance.

<stopping criteria details>


A1 =

   -1.0000
    0.0003


A2 =

   -0.7628
   -0.1556


A3 =

   -0.3281
   -0.3879
Nom : untitled.jpg Affichages : 292 Taille : 14,7 Ko

ce qui est totalement puisque normalement les position des aimants 2 et 3 devraient être [+/- sqrt(3)/2 ; 0,5 ]

Merci d'avance pour votre aide !