Bonjours ,
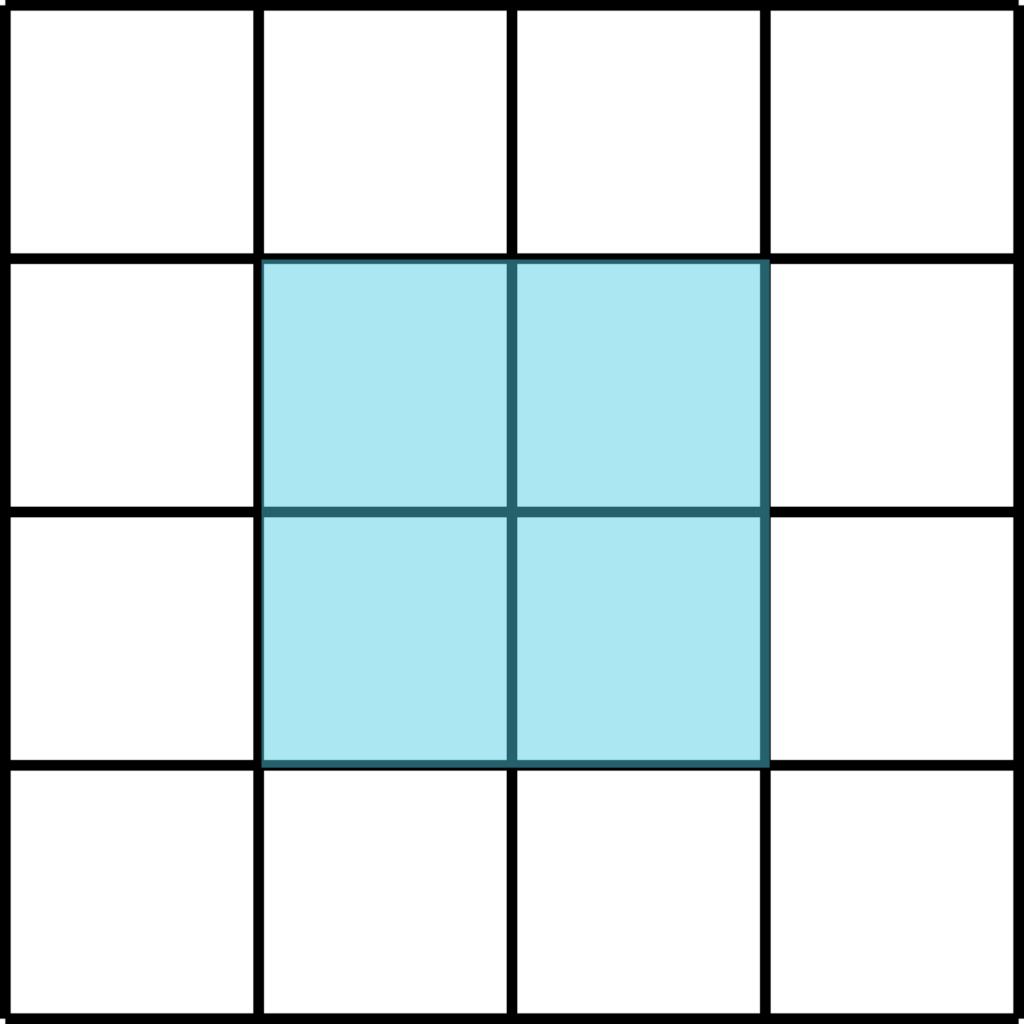
j'aimerais que vous puissiez me donner un algorithme permettant de remplir un carré de dimension n² x n² remplie de tous les entier de 1 à n^4 , et dont la somme des nombres de chaque carré n x n est constant , merci .
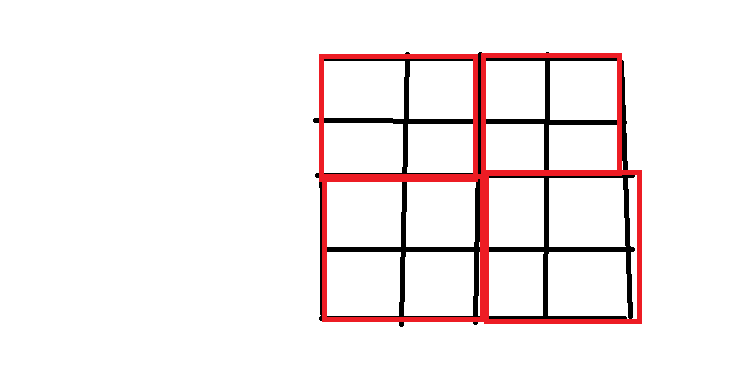
Édit: aucun carré n x n n'est confondu partiellement ou totalement
Dernière modification par gienas ; 11/03/2017 à 12h29. Motif: Édit à la demande de l'auteur
Bonjour,
Qu'entendez-vous par "algorithme" ?
Si c'est au vrai sens, c'est à dire suite des actions et tests pour résoudre ce problème, ce peut être un défi à lancer.
Si c'est un programme que vous espérez, là je pense qu'il y ait peu de chance que vous ayez une réponse.
Tu bloques où ?
Ca ressemble plus à une question de math que d'info.
Je ne bloque pas , je voudrais comparé l'algorithme que j'ai trouvé au votre .
Alors donne le tien parce qu là on a l'impression que tu veux nous faire résoudre un exercice.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
Je peux le donner mais pour éviter que ceux des autres soit inspirer du mien je le donnerais dans une archive avec mot de passe je donnerais le mot de passe quand je le déciderais mais je le donnerais .
C'est bien ce que je pressentais : un exercice. Et surtout garder pour soi les résultats. Il ne faut pas que les copains copient.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
Déja, je ne comprend pas le problème.Envoyé par 610987
Qu'est-ce qu'un "carré" ?
Remplir un tableau du type x[1..n, 1..n, 1..n, 1..n] , ou autre manière de présenter, array[1..n] of array[1..n] of array[1..n] of array[1..n], comme en pascal, ok.
Avec des entiers au choix allant de 1 à n^4, ok.
Mais "dont la somme de chaque carré n x n ... ", pas ok, pour moi ça ne veut rien dire.
Si c'est claire chaque carré n x n soit les n^2 carrés n x n doivent contenir n^2 entier dont la somme est constante dans tous les carré n x n.
Et tu penses qu'il va mieux comprendre en lui répétant exactement la même phrase ?
Par exemple, dans un carré 4x4, tu comptes combien de carrés 2x2 ?
C'est simple 4 .
C'est pas si simple tu vois, j'en compte 5.
Tu te trompe il y a quelque soit n toujours n^2 carré n x n dans un carré n^4 .
regarde ca.
Voilà j'ai terminé mon algorithme , ca prouve que je ne suis pas un tricheur maintenant j'attend des solutions :
carré.zip
.
je vois ce que tu veux dire par 5 carrés mais tu te trompe il y en a 9 , et quand j'ai dit 4 j'ai dit aucun carré n'est confondu partiellement ou totalement , c'est ça que l'on considère ici.
Il y a une raison pour ne pas considerer ce carré ?
Ah, mais ça tu ne l'avais pas précisé au début... Ca change en cours de route...
Et du coup c'est beaucoup plus simple de régler le problème, ça devient même enfantin.
Lie mes précédent message au lieu d'écrire si rapidement n'importe quoi , parce qu'il n'y aucune raison également de ne pas considérer 4 carré supplémentaires .
Tu peux commencer .
tu voit que c'est faux maintenant .
Personne ?
Presque 600 affichages et personne ne donne de solution .
Si il vous plait répondez , si vous être capable de résoudre ce problème .
Salut,
Il me semble que ton histoire relève de l'arithmétique.
Il me semble qu'il faut en premier lieu démontrer que ton histoire tient la route.
Si c'est le cas l'algorithme coule de source. n2 c'est quoi ?
Cordialement
Ludwig
Salut,
il semblerait que je ne sois pas seul à ne pas comprendre l'histoire.
Quelques explications complémentaires s'imposent je crois
Cordialement
Ludwig
Bonjour ,
Les carré n x n commencent en haut à gauche puis complètent le rectangle de dimension n x n^2 , en s'ajoutant l'un après l'autre , puis le rectangle de dimension n x n^2 juste en bas ... , jusqu'à compléter le carré n^2 x n^2 , la somme des entiers dans un carré n x n est constante pour tous les autre carré
n x n du carré n^2 x n^2 .
Et j'ai modifié mon premier message pour rendre l'énoncé plus claire .
Je vais répéter la question posé depuis le début, où bloquez-vous ?
Le problème est enfantin. Quelques secondes m'ont suffit, et je ne suis pas un génie des math.
Je ne bloque pas j'aimerais voire vos solutions .
Sauf que tu dis en avoir une et que tu ne veux pas la montrer publiquement. Sais-tu quel doit être l'esprit d'un forum ? j'en doute.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
JPL vous voulez dire l'esprit de CE forum , en plus ça n'est pas juste censé être un forum pour poser des questions .
Je donnerais le mot de passe au bout de quelque solutions ça dépendra .
Un forum c'est un lien de partage et toi tu viens y faire tes courses.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
