Bonjour à tous,
Après des heures de recherches, je ne trouve pas de réponses à mon problème.
J'exploite et je traite un signal reçu sur la voie série, rien de bien compliqué.
Je souhaite en faire une transformée de Fourrier.
Les valeurs recues sont des tensions analogiques déjà échantillonnées par un CAN 16 bits, à 25Hz. Je convertis ces valeurs en un signal d'angle en fonction du temps.
J'ai donc un tableau de valeurs et un tableau des temps correspondants.
Comment à partir de ces deux tableaux faire un FFT grâces aux bibliothèques disponibles sous python ?
Avec un signal continu, et un échantillonnage j'ai trouvé ce programme que je comprends à peu près ( pas assez pour l'adapter à mon problème).
Sauriez-vous m'aider ?
Merci d'avance !
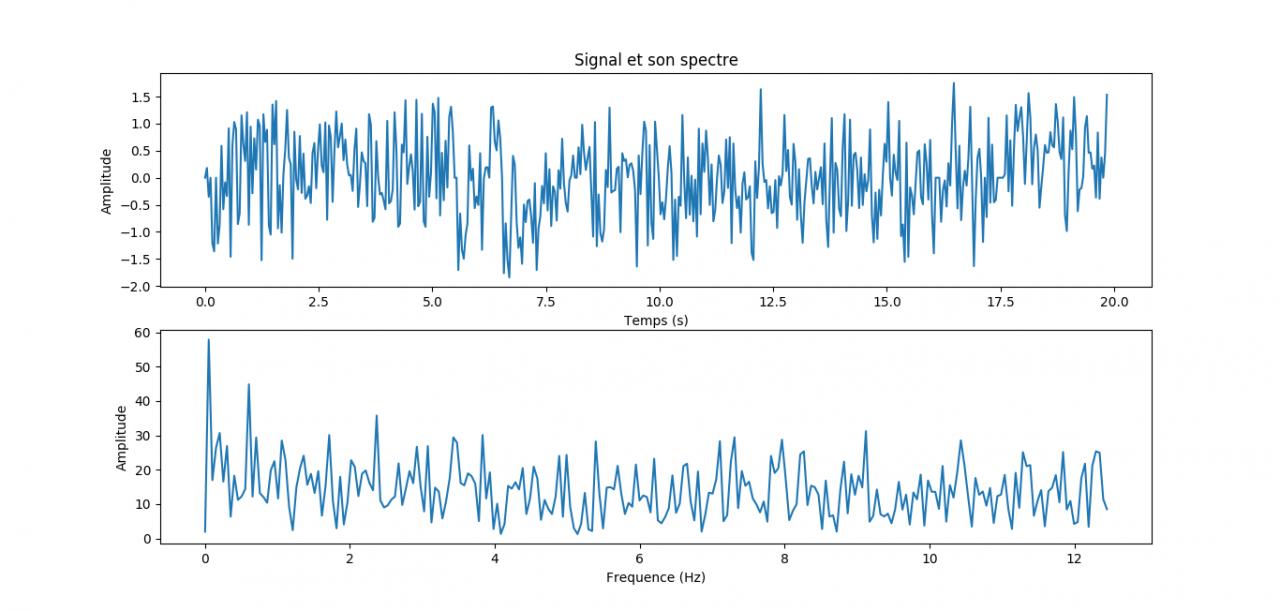
Voilà ce que je veux pour mon signal : figure_1.pngCode:# programme d'experimentation FFT FFTExperience1-0 # Dominique Lefebvre pour TangenteX.com # 12 aout 2014 # # importation des librairies from numpy import pi, sin, linspace, log10 from numpy.fft import fft, fftfreq import matplotlib.pyplot as plt # d�finition des constantes du signal K = 2*pi # facteur conversion p�riode/fr�quence A0 = 4 # amplitude fr�quence fondamentale A1 = 8 # amplitude premi�re harmonique f0 = 2 # fr�quence fondamentale (Hz) f1 = 8 # fr�quence premi�re harmonique (Hz) # d�finition temporelle du signal t0 = 0 # d�but de l'acquisition du signal t1 = 10 # fin de l'acquisition (s) # d�finition des param�tres d'�chantillonnage FreqEch = 1024 # fr�quence d'�chantillonage PerEch = 1./FreqEch # p�riode d'�chantillonnage N = FreqEch*(t1 - t0) # nombre de points �chantillonn�s sur l'intervalle # d�finition du temps t = linspace(t0, t1, N) # d�finition du signal signal = A0*sin(f0*K*t) + A1*sin(f1*K*t) # d�finition des donn�es de FFT FenAcq = signal.size # taille de la fenetre temporelle # calcul de la TFD par l'algo de FFT signal_FFT = abs(fft(signal)) # on ne r�cup�re que les composantes r�elles # r�cup�ration du domaine fr�quentiel signal_freq = fftfreq(FenAcq,PerEch) # extraction des valeurs r�elles de la FFT et du domaine fr�quentiel signal_FFT = signal_FFT[0:len(signal_FFT)//2] signal_freq = signal_freq[0:len(signal_freq)//2] #affichage du signal plt.subplot(211) plt.title('Signal et son spectre') plt.ylim(-(A1+5), A1+5) plt.plot(t, signal) plt.xlabel('Temps (s)'); plt.ylabel('Amplitude') #affichage du spectre du signal plt.subplot(212) plt.xlim(0,f1+5) plt.plot(signal_freq,signal_FFT) plt.xlabel('Frequence (Hz)'); plt.ylabel('Amplitude') #plt.title('Signal et son spectre') plt.show()
Voici mon code python et l'allure de mon signal :
figure_1bis.jpgCode:import serial import matplotlib.pyplot as plt import time import numpy as np from numpy.fft import fft, fftfreq signal=[] temps=[] serie=serial.Serial('COM5',9600) # ouvre une liaison serie en 9600bps plt.style.use('bmh') plt.ylabel("Delta (°)") plt.xlabel("Temps (sec)") plt.ion() # on entre en mode interactif start=time.time() # mesure de l'instant initial i=0 while (i<400): mesure1, mesure2 = map(float, serie.readline().split()) #lit la donnee sur la laison serie angle1 = mesure1 / (1/180) #conversion tension - degrés (2V = 360°) angle2 = mesure2 / (1/180) if i == 3: #les premières mesures ne sont pas fiables ref = (angle2-(angle1)*(1/25)) #différence entre theta et theta_theorique if abs(angle1) <= 1: ref = (angle2-(angle1)*(1/25)) instant=time.time()-start # calcul du temps ecoule depuis l'instant initial if i >= 3: temps.append(instant) # ajout de instant a la liste des temps valeur = (angle2-(angle1)*(1/25))-ref #on veut un écart autour de 0 if abs(valeur) >= 1.5: valeur = 0 signal.append(valeur) print(valeur,instant) # affiche dans la console les coordonnees du point plt.plot(temps,signal,marker='') # trace la courbe plt.draw() # affiche la courbe en mode interactif i=i+1 plt.show() plt.ioff() # on quitte le mode interactif pour rendre la main a l'utilisateur sur la courbe
-----




 ...
... )
)