J'ai besoin de résoudre par la méthode de différences finies l'équation dans le fichier ci-joint.
Lien supprimé
Le but est d'avoir 3 vecteurs :
- x composé de M+2 blocs identiques chacun comportant xi de i = 0 à i = N+2
- y composé de M+2 blocs chacun comportant N+2 fois la valeur tj = j * Delta t
- Z composé M+2 blocs chacun comportant les valeurs de u(xi,tj) pour tj fixé et i de 0 à N+2
ces vecteurs seront utilisés pour le traçage du plot 3D de u(x,t).
Voici mon code :
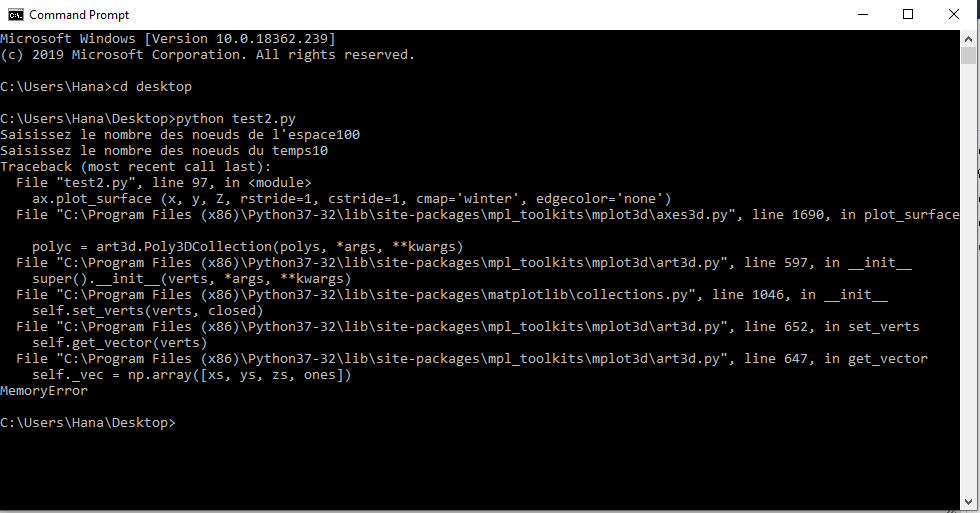
Pour N = 10 et M =10, le code marche parfaitement. Mais, pour N = 100 et M =10, j'obtiens un Memory error.Code:import numpy as np import scipy.sparse as sps from scipy.sparse.linalg import spsolve ** ** # Saisie des inputs par l'utilisateur c = -1 e = 1 L = 1 T = 1 U0t = 2 ULt = 1 Ux0 = 1.5 N = input ("Saisissez le nombre des noeuds de l'espace") N = int (N) M = input ("Saisissez le nombre des noeuds du temps") M = int (M) ** # Calcul du pas de l'espace h = L/(N+1) ** # Discrétisation de l'intervalle [0,L] selon le pas h X = np.linspace (0.0,L,N+2) ** ** # Calcul du pas du temps t = T/(M+1) ** ** # Remplissage de A matrice tridiagonale symétrique de taille N*N def tridiag(P, Q, R, k1=-1, k2=0, k3=1): ****N = len(Q) ****return (sps.spdiags(P,-1,N,N) + sps.spdiags(Q,0,N,N) + sps.spdiags(R,1,N,N)) ** P = (1/h**2)*np.ones(N) ** Q = (c - 2/h**2)*np.ones(N) ** A = sps.csc_matrix(tridiag(P,Q,P)) ** ** # Remplissage de B vecteur colonne de taille N B = np.zeros(N) B[0] = (1/h**2)*U0t B[N-1] = (1/h**2)*ULt ** ** # Initialisation de Uj à l'instant tj=0 U = Ux0*np.ones(N) ** # Nouvelle A A = sps.csc_matrix((e/t)*np.eye(N) - A) ** ** # Intialisation de x, y = t et Z = u (x,t) à l'instant y = t = 0 ** x = X y = np.zeros(N+2)** z = np.insert (U,0,[U0t]) z = np.append (z,[ULt]) Z = z ** # Calcul de Uj+1 à partir de Uj ** for j in range (1,M+2): ****# Insertion du jème bloc des xi* ****x = np.append(x,X) ****# Insertion du jème bloc de tj ****y = np.append(y,[j*t*np.ones(N+2)]) ****# Calcul de Uj à partir de Uj-1 ****V = (e/t)*U + B ****U = spsolve(A,V) ****U = np.ravel(U) ****# Insertion de u(0,tj) et u(L,tj) ****z = np.append (U,[ULt]) ****z = np.insert (z,0,[U0t]) ****# Insertion du jème bloc de u(xi,tj) ****Z = np.append (Z,z) ** ** # Traçage du plot 3D de u(x,t) ** Z = np.reshape(Z,((N+2)*(M+2),1)) ** from mpl_toolkits import mplot3d import matplotlib.pyplot as plt ** fig = plt.figure() ax = plt.axes(projection="3d") ax.plot_wireframe(x, y, Z, color='green') ax.set_xlabel('x') ax.set_ylabel('t') ax.set_zlabel('u') ax.plot_surface (x, y, Z, rstride=1, cstride=1, cmap='winter', edgecolor='none') ** plt.show()
Comment faire pour résoudre ce problème ?
Merci de votre aide
-----