comment définir une surface dans l'espace

[Praesilia]

Bonjour a tous/toutes,

Je post ici a propos d'un problème nécessitant un niveau de math bien supérieur au mien mais surement très abordable pour les lecteurs de ce forum.

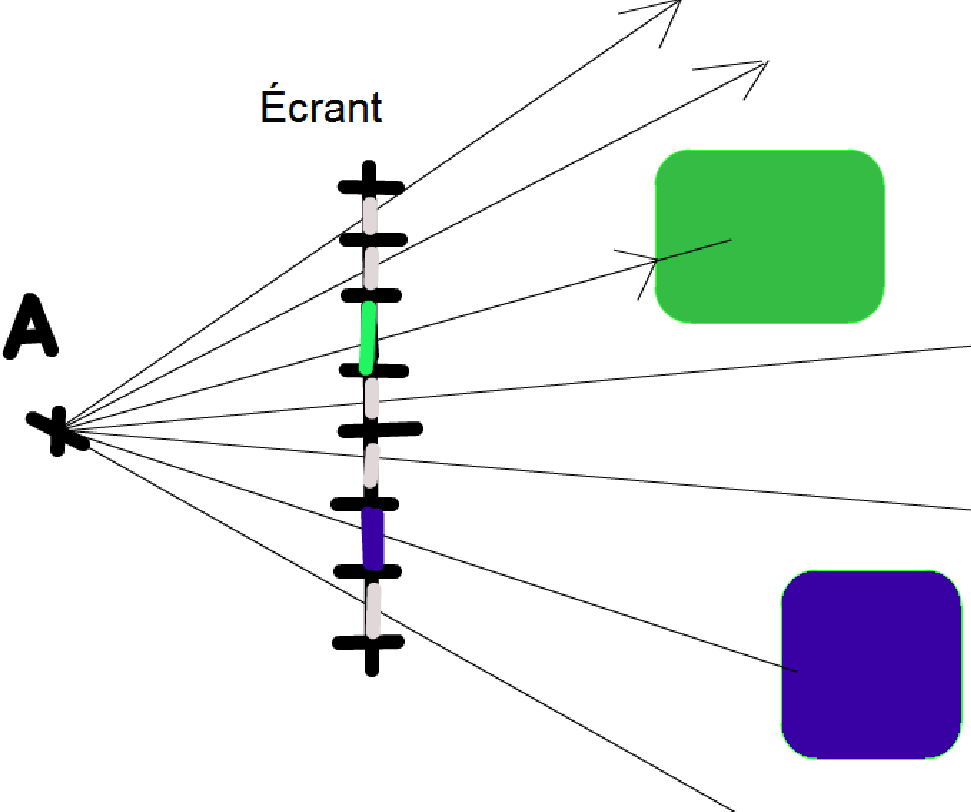
Je suis actuellement sur un projet informatique visant a coder un moteur de vue 3D mais je me trouve face a un problème:
je ne sais pas définir mathématiquement une surface finie sans courbes, plane dans un espace a trois dimensions.

Je sais comment obtenir l’équation d'un plan, je suis au point sur les vecteurs/produit scalaire et autre joyeuseté du début de licence (chimie, pas math pour ceux qui se demandent) mais je ne vois pas comment arrêter la surface de mon plan le long d'une ligne (le long d'une courbe je m'en fout, sauf si c'est aussi simple, mais j'en doute fortement)
L'idée étant au final de pouvoir calculer si il y a intersection entre la surface et un vecteur, je vous serais très reconnaissant de m'aider a trouver la forme mathématique la plus adaptée a mon problème


Merci d'avance pour votre aide !
-----

[Dlzlogic]

Bonsoir,
Votre question manque de précision.
Qu'appelez_vous une surface finie ? La représentation la plus habituelle et la plus facile à utiliser est une surface constituée de triangles. Un polygone [plan] peut toujours être divisé en triangles. Si un polygone n'est pas plan, il faut le diviser en triangles. Il y a deux configurations possibles, longitudinale, comme le serait une route et centrée, comme le serait un parking de grande surface.
Un triangle est un ensemble de trois points en XYZ défini dans un sens conventionnel. C'est à dire qu'on peut distinguer le côté pile du côté face (ou le dessus du dessous).
Pour ce genre de représentation, une courbe est toujours transformée en polygone dont la longueur des côtés dépend de la précision voulue et de rien d'autre. Autrement dit, cette division ne concerne que la représentation.
D'après la suite de ce que vous dites, votre préoccupation est ce qu'on appelle le problème des surfaces cachées.
Un conseil, oubliez les notions d'équation de plan, de vecteurs etc. Ramenez tout à des triangles et traitez les triangles. C'est à dire l'objet à traiter est "le triangle". Pour faire les opérations informatiques, tous les outils sont à disposition, sauf à se focaliser sur certains.
Par ailleurs, il existe, je suppose, des logiciels qui font ça. Telle que votre question est posée, je suppose que ce n'est pas ce que vous cherchez.
Ce n'est pas un problème vraiment facile, ce qui est important est de partir de bonnes bases.
Comme vous vous en doutez, j'ai développé cela, donc n'hésitez pas à poser des questions.

[Praesilia]

tout d'abord, merci pour votre réponse.

Comme vous l'avez deviné je ne cherche pas de logiciel traitant ce problème a ma place, l'idée étant de le faire moi-même

Donc si je comprend bien, plutôt que de composer avec des surfaces de formes differentes, je compose avec des triangles définis par leurs trois extrémités ? Ca parait plus simple effectivement, mais je ne vois pas comment calculer ce que vous appelez le "problème des faces cachée".

apres un petit tour sur wikipedia:
https://fr.wikipedia.org/wiki/D%C3%A...s_cach%C3%A9es

l'idée du "Viewing frustum culling" m’était déjà venue a l'esprit (pas besoin d'avoir bac+38 pour savoir qu'on ne voit pas un objet qui se trouve derrière la camera ), mais je bloque pour savoir comment un de mes triangle en cache un autre.

Mon idée de base était:
- Prendre un point A et le définir comme origine de la camera
- Faire partir plusieurs vecteurs, tous d'origine A, et passant tous en un point différent d'une grille X/Y ou X = résolution largeur de l’écran et Y = résolution hauteur de l'écran.
- vérifier quel est la première face que le vecteur croise
- donner la couleur de cette face au point de coordonnée X/Y de la grille

et au final on obtient une image de résolution x/y
Petit schéma 2D pour plus de clarté:


Image supprimée

(un petit T fougueux est apparut a la fin d'écran, pardonnez le)

Mais avec cette méthode il faut faire beaucoup de calcul pour tester les collision entres les vecteurs et les faces, du coup je ne sais pas si c'est très adaptée... Si vous avez mieux ( et vous avez surement mieux !) je suis preneur !
Encore merci pour votre aide et merci d'avance pour vos réponses

[JPL]

Les illustrations doivent être postées en pièces jointes et non sur un serveur externe. Merci.

[A voir en vidéo sur Futura]

[Praesilia]

Réupload de l'image en pièce jointe (désolé pour le doublon)

[Dlzlogic]

Bonjour,
J'ai lu deux thèses sur le sujet, la seconde faisant référence à la première.
Tous les détails ne sont plus très clairs dans mon esprit. Mon programme date d'une quinzaine d'années. Je connaissais la méthode des "rayons lancés", personnellement je préfère une méthode plus pas à pas, c'est à dire que les triangles sont tels qu'il n'y a par d'intersection entre eux. Un triangle peut en cacher un autre, ou pas etc. Ce type de test est rapide. Par contre, en aucun cas tester pixel par pixel.
Vous ne m'avez pas dit si vos objets étaient en 3D vrai, comme une pièce mécanique qui ignore la verticale, ou en 2.5D où la verticale est une réalité et où on doit en profiter.
Pour être efficace dans les calculs, il faut, à tout instant, les faire dans un plan. Soit 2 triangles A et B, on sait qu'ils ne s'intersectent pas. Chaque triangle firme une pyramide de base A ou B et a le même sommet, la caméra. il est rapide de tester les différents cas possibles. Ponsez toujours à projeter que le plan horizontal puis sur le plan vertical, passant par la caméra.
Petit secret, c'est l'un de mes sujets favoris, ne le répétez pas.

[Praesilia]

Bonjour,
deja un premier point pour clarifier: je n'ai rien codé, je reflechis sur papier a comment coder correctement, avant de me lancer tete baissée, donc rien n'existe

L'idée est quand meme de creer de la 3D, pas de la 2,5D. Ce que je ne comprend pas, c'est le test specifique a effectuer entre les triangles et la camera pour savoir lequel est le plus proche. Et je ne comprend pas non plus comment retranscrire le resultat de ce calcul (C'est a dire: quel triangle est le plus proche) en affichage, sans passer par une analyse pixel par pixel.

Si vous pouviez m'eclairer sur ces sujets je vous en serais infiniment reconnaissant.

Merci beaucoup pour votre aide, et par avance pour l'aide que vous m'apporterez, en vous souhaitant une bonne fin de journée

[ansset]

c'était la base des premiers logiciels 3D : coder la vue d'un ensemble de triangles vue depuis un point fixe.
commence par rechercher ce que donne la vue d'un seul triangle , qui est bêtement défini par 3 points qcq.
c-a-d, que donne la projection (selon les coord sur le plan que tu choisis ) des trois points sur "l'écran" de vision en fonction de leurs coord et des angles ( vert , horiz ) de vision.(*)
(*) tu peux aussi prendre l'angle horiz et le rapport H/L , ce qui revient au même.

[minushabens]

Il y a déjà pléthore de moteurs de rendu 3D, je ne vois pas l'intérêt d'en créer un nouveau. Mais quoi qu'il en soit, certains sont open-source et de toutes façons les algorithmes de base sont publiés. Du temps où je m'intéressais un peu à la question, un bouquin de référence était le Foley & van Dam. Mais ça doit être dépassé...

[ansset]

Il y a déjà pléthore de moteurs de rendu 3D, je ne vois pas l'intérêt d'en créer un nouveau. Mais quoi qu'il en soit, certains sont open-source et de toutes façons les algorithmes de base sont publiés. Du temps où je m'intéressais un peu à la question, un bouquin de référence était le Foley & van Dam. Mais ça doit être dépassé...

ben , justement, ça me semble correspondre à la démarche initiale de Praesilia.
les bases antiques !

[Dlzlogic]

Bonjour,

L'idée est quand meme de creer de la 3D, pas de la 2,5D. Ce que je ne comprend pas, c'est le test specifique a effectuer entre les triangles et la camera pour savoir lequel est le plus proche. Et je ne comprend pas non plus comment retranscrire le resultat de ce calcul (C'est a dire: quel triangle est le plus proche) en affichage, sans passer par une analyse pixel par pixel.

En fait, la seule distinction important entre 3D et 2.5D est la prise en considération de la notion de verticale et d'horizontale. Avec la 3D, cette notion n'existe pas, par ex un hélice de bateau ou un avion de voltige, par contre un ballon aura toujours sa nacelle sous le ballon. Rien n'interdit de tourner autour d'un objet mais un objet 2.5D aura toujours une verticale.

Si vous faites un dessin avec le point de caméra et le point visé, c'est à dire le centre du rectangle correspondant à l'écran, qu'il faut comparer à une fenêtre par laquelle vous regardez et un point quelconque, cette droite va rencontrer 2 triangles. ces triangles ne se coupent pas, donc il n'y a pas de doute sur leur position relative par rapport à la caméra. Il n'y a qu'à calculer les deux distances et comparer.

Donc, supposons que votre objet est bien divisé en triangles. Dans le cas général, ils auront deux à deux un côté commun. Chaque triangle, outre la liste des 3 points qui le constitue devra posséder des caractéristiques, par exemple l'objet auquel il appartient, sa couleur, ses voisins etc. Il faudra prévoir une caractéristique, telle "Vu à un instant donné". Quand un triangle est caché, ce ne sera plus la peine de le tester.

[LeMulet]

L'idée est quand meme de creer de la 3D, pas de la 2,5D. Ce que je ne comprend pas, c'est le test spécifique a effectuer entre les triangles et la camera pour savoir lequel est le plus proche. Et je ne comprend pas non plus comment retranscrire le résultat de ce calcul (C'est a dire: quel triangle est le plus proche) en affichage, sans passer par une analyse pixel par pixel.

La question est : Pour quoi faire ?

Ce qu'il faut comprendre ici, c'est que le "triangle" est l'unité de base gérée par les cartes graphiques.
Il est inutile de vouloir gérer un certain nombre de traitements, qui sont effectués à la vitesse de l'éclair (les cartes graphiques sont multiprocesseurs, multitâches, avec des algorithmes dédiés au traitement 3D).
On appelle ça "le" GPU.
Le CPU, lui, c'est l'ordinateur, et il faut éviter de lui faire faire des traitements inutiles (il en a déjà assez à faire, même dans une application 3D gérée par le GPU)

Au niveau traitement GPU :
Le triangle est "mappé" à plat sur le "plan de vue" (l'écran en gros) au niveau pixel (qui est l'unité de base d'affichage).
Or les cartes graphiques savent décider quel pixel se trouve "au dessus" d'un autre relativement au "point de vue" gràce à un buffer de profondeur, un DEPTH BUFFER.
Si le pixel se trouve "au dessus" d'un autre (traduisez, "derrière" relativement au point de vue) il efface le pixel invisible de la bitmap à plat (celui qu est affiché sur l'écran).

Ceci n'est valable QUE si le pixel est opaque (3 couleurs, r,g,b) mais échoue à la tâche si le pixel est transparent (4 couleurs r,g,b,a)
C'est dans ce cas de figure et uniquement dans ce cas de figure, que vous avez besoin de savoir quel "forme" (le triangle en occurrence ici) se trouve devant l'autre.
Ceci afin d'envoyer les données d'affichages les triangles dans le bon ordre (du plus lointain au plus proche).
Cette méthode n'a pas de solution générale, puisque dans le cas général les triangles peuvent se recouper et qu'il faut alors découper les trangles... l'horreur quoi. )

De la même manière, si un triangle ne se trouve pas "dans le bon sens", comprenez par là ; que le vecteur normal au plan du triangle est dans le sens contraire à la "direction de la vue", depuis le point de vue, alors le GPU décide de ne pas traiter ni afficher le triangle (qui est une unité de base dans le traitement, comme dit précédemment).
Ceci à condition d'avoir demandé à la carte de le faire... en openGL, on active le "Cull Face", par exemple glenable(GL_CULL_FACE).
Donc là, attention, un triangle doit être "orienté", (sinon, vous comprenez bien qu'un triangle aurait deux vecteurs normaux possibles)

Maintenant, pour ce qui est des traitements mathématiques, produites par le CPU (ou envoyés au GPU pour libérer le CPU mais là c'est d'un niveau de programmation assez costaud avec le langage GLSL), ils peuvent être effectivement utiles.
Mais pas pour l'affichage à proprement parler.
Par exemple pour décider quels sont les "primitives" (les triangles) à envoyer dans la mémoire du GPU (de manière à accélérer l'affichage), certains pouvant être hors du cadre d'affichage (derrière le point de vue, sur le côté etc)
Ou typiquement dans une application 3D pour savoir quel objet visible est pointé si on ne veut pas pouvoir traverser les objets qui se situent sur le chemin de la vue.

Donc comme dit : Pour quoi faire ?
Que fait le programme ?
A partir de là, on peut commencer à parler mathématiques et effectivement il y a de nombreuses méthodes adaptées à chaque cas.

[ansset]

Bonjour,
J'ai lu deux thèses sur le sujet, la seconde faisant référence à la première.
Tous les détails ne sont plus très clairs dans mon esprit. Mon programme date d'une quinzaine d'années. Je connaissais la méthode des "rayons lancés", personnellement je préfère une méthode plus pas à pas, c'est à dire que les triangles sont tels qu'il n'y a par d'intersection entre eux. Un triangle peut en cacher un autre, ou pas etc. Ce type de test est rapide. Par contre, en aucun cas tester pixel par pixel.
.

!!!! c'est pourtant à la base des logiciels , balayage en ligne et en colonne.
me demande si tu as toi même programmé un logiciel de ce type ( ou plutôt de celui que tu proposes ).
Cdt

[ansset]

ps : deux triangle n'ont pas besoin de s'intersecter pour qu'une partie de l'un cache une partie de l'autre.

[Dlzlogic]

Bonjour LeMulet,
Par rapport à la question initiale, on a déjà bien avancé. On est parti de surface dans l'espace à triangle caché. Ne brulons pas trop vite les étapes.
Un point important, évident, mais ça va mieux en le disant : il n'y a que les triangles qui constituent des plans. C'est à dire, sauf cas particulier, un quadrilatère dans l'espace n'est pas plan. Autre point utile à rappeler est qu'une courbe sur un écran, sera toujours un polygone.
D'après ce que j'ai compris, Prescillia voudrait étudier les notions à la base pour être sûr de les comprendre. Et sur ce point, on ne peut que l'approuver.

[Dlzlogic]

A propos de triangles.
C'est un problème que je connais un peu. En 86, j'ai encadré le projet de fin d'étude d'un binôme de l'école des Mines de Douai. A cette époque, nous n'avions pas d'écran graphiques, il y avait bien les Tecktonik, mais mon service n'y avait pas accès.
La question de division de triangles est effectivement fondamentale. Il est bien évident que deux triangles n'ont pas besoin de s'intersecter dans l'espace pour que l'un cache une partie de l'autre. Mais en fait, cette question doit venir en amont, si des triangles constituent la représentation d'un objet, alors il est impossible que deux triangles se coupent.
Il est rare que l'on travaille au niveau du pixel. Cela ne se fait que pour des cas particuliers, par exemple le traitement d'images raster. D'ailleurs, il est nécessaire de trouver des techniques particulières.
A mon avis, ce point ne concerne pas la demande de Praecillia. L'unité de travail doit être la facette triangulaire.
D'autre part, si on travaille au niveau du pixel, on travaille au niveau de l'écran et non pas d'une vue de l'objet.

[LeMulet]

je ne sais pas définir mathématiquement une surface finie sans courbes, plane dans un espace a trois dimensions.

Et pour quand même répondre à cette question, au cas où vous voudriez faire un "moteur 3D antique".
Personne ne sait définir mathématiquement cet objet (en tous cas, pour ma part je n'ai jamais vu personne modéliser cet objet, ce qui serait pratique on est d'accord)

Par contre sait définir un plan et on sait vérifier si un point se trouve "devant" ou "derrière" un plan (notion qu'il vous faut comprendre)

Donc ici, si vous voulez un début de réponse à votre question (indépendamment de l'aspect GPU), à savoir, est-ce qu'une droite intesecte avec un triangle, il faut procéder par étapes.
D'abord, vous cherchez les point d'intersection entre la droite et le plan de ce triangle.
Ensuite, vous vérifiez si le point trouvé se trouve dans ce triangle en vérifiant successivement que ce point se trouve "devant" les 3 plans composés de la manière suivante: Du point de vue et de deux points du triangle. (ce qui fait 3 test pour les trois plans des trois faces de la "pyramide" (du tétraèdre en fait).

Pour obtenir les équations de ces 3 plans :
Vous prenez les trois points indiqués plus haut et produisez un plan, qui sera alors orienté, par l'ordre des points passés à la fonction qui retourne l'équation du plan
Ensuite (et pour peu que vous ayez passé les points à la fonction dans le bon ordre), vous vérifiez si le point d'intersection trouvé précédement pour le triangle de recherche, se trouve devant ou derrière le plan.
Le "bon ordre", c'est celui qui est cohérent.
Je m'explique : Vous devez vous placer mentalement en face du triangle qui va définir le plan, puis CHOISIR un sens de rotation, et toujours garder ce sens (comme ça, c'est "cohérent").
Vous passez à la fonction les positions (points) des sommets du triangle dans le sens dextrogyre par exemple, ou dans le sens levrogyre, au choix (mais toujours le même)

Pour établir ces deux fonctions, il est nécéssaire de choisir la bonne représentation pour un plan (il y a plusieurs formules possibles).
Exemples tout faits en Pascal pour savoir si un point est devant un plan (en équation paramétrique, je crois qu'on appelle ça comme ça):

//****************************************************************************//
//** Retourne Vrai si la position passée en v est devant le plan défini     **//
//** par l'equation parametrique du plan                                    **//
//****************************************************************************//
function EstDevantPlan(v: TVector; p: TPlan): boolean;
begin
  if p.a*v.x + p.b*v.y + p.c*v.z + p.d<0.0 then EstDevantPlan:=false else EstDevantPlan:=true;
end;

//****************************************************************************//
//** Retourne les quatres coeficients de l'equation d'un plan               **//
//** d'apres 3 points  du plan passes en parametre                          **//
//****************************************************************************//
function EquationPlanPoints(v1,v2,v3: TVector): TPlan;
begin
  EquationPlanPoints.a:=v1.y*(v2.z-v3.z) + v2.y*(v3.z-v1.z) + v3.y*(v1.z-v2.z);
  EquationPlanPoints.b:=v1.z*(v2.x-v3.x) + v2.z*(v3.x-v1.x) + v3.z*(v1.x-v2.x);
  EquationPlanPoints.c:=v1.x*(v2.y-v3.y) + v2.x*(v3.y-v1.y) + v3.x*(v1.y-v2.y);
  EquationPlanPoints.d:=-(v1.x*(v2.y*v3.z-v3.y*v2.z) + v2.x*(v3.y*v1.z-v1.y*v3.z) + v3.x*(v1.y*v2.z-v2.y*v1.z));
end;

Reste à coder la fonction qui donne le résultat de l'intersection d'une droite (en équation paramétrique) avec un plan.

[ansset]

Je ne saisi pas précisément le but de Praesilia.
s'il s'agit pour elle de programmer elle même un moteur 3D de base, tout en comprenant le B.A.BA on peut effectivement se procurer la dernière version ( certes ancienne ) du Foley & Van Dam ( et Hugues ).
Cette version donne en plus des bouts de code en C.
Je n'ai pas ouvert ce livre, donc je ne connais pas l'étendu des propositions de programmation.

[Praesilia]

Bonjour,

Je me suis absenté assez longtemps de répondre pour observer les differentes idées proposées ici.
Alors deja je clarifie: oui je parle de réinventer la roue, ce que je cherche a faire a déja été fait plusieurs fois et bien mieux que ce que je ne ferai jamais (donc je réinvente une roue moche).

Le but est de comprendre comment fonctionne un moteur a la racine même de l'idée, et essayer de voir comment en creer un moi-meme (Et oui pour ceux que ca inquiete, le moteur tournera sur le CPU, parce que quand on est pas tres fort en programmation on ne sait pas allouer le calcul a la carte graphique)
On reste calme, la santé de mon ordinateur n'est pas en danger, si j'arrive afficher une pyramide je serait content (on en est pas au niveau d'une foret ou autre scene a 12M de triangles....)


Du coup j'ai avancé de mon coté et j'ai fait deux choses:
- j'ai calculé comme projeter les coins d'un triangle qui est dans le champs de vision sur l'ecrant (en reprenant mon idée de faire partir des vecteurs, sauf que je projete sur l'ecrant, c'est effectivement bien mieux)

-j'ai calculé comment modifier les coordonées des points en fonction des déplacement rectilignes et angulaires et de ma camera.

Ce dernier point semble peut etre illogique, en fait je ne sait pas comment m'y prendre. La camera doit pouvoir se deplacer, sinon je créé un rendu qui est une seule image fixe d'une scene 3D.
Mais en déplacant ma camera je me trouve face a un probleme: dois-je définir le repère de mes coordonées sur ma camera, et faire varier la position de toutes les coordonées de tous polygone du monde en fonction des mouvements de la camera, ou doit-je positionner les objets par rapport a un repère arbitraire, et calculer a la volée pour chaque triangle dans mon champs de vision, les nouvelles coordonées par rapport a la camera, avant de projeter ?

J'etais partit sur la deuxieme option mais je ne sais pas si elle est trop gourmande en calcul. Je ne sais pas non plus si il existe une alternative.

Je m'en remet donc a vous,
cordialement

[ansset]

-j'ai calculé comment modifier les coordonées des points en fonction des déplacement rectilignes et angulaires et de ma camera.

Ce dernier point semble peut etre illogique, en fait je ne sait pas comment m'y prendre. La camera doit pouvoir se deplacer, sinon je créé un rendu qui est une seule image fixe d'une scene 3D.
Mais en déplacant ma camera je me trouve face a un probleme: dois-je définir le repère de mes coordonées sur ma camera, et faire varier la position de toutes les coordonées de tous polygone du monde en fonction des mouvements de la camera, ou doit-je positionner les objets par rapport a un repère arbitraire, et calculer a la volée pour chaque triangle dans mon champs de vision, les nouvelles coordonées par rapport a la camera, avant de projeter ?

J'etais partit sur la deuxieme option mais je ne sais pas si elle est trop gourmande en calcul. Je ne sais pas non plus si il existe une alternative.

Je m'en remet donc a vous,
cordialement

c'est un bel objectif quand même de recréer un logiciel de base.

pour répondre à ta question:
concernant la caméra :
elle doit être définie par : ( outre le ratio 4/3 ; 16/9 , etc )
-sa position
-sa direction de visée
-son angle. ( horizontal par ex , ce qui donne le vertical avec le ratio , par trigo )
pour la direction , on a le choix entre des angles, ou une "mire" ( point regardé )
en général, on utilise la mire :
plus facile quand on tourne autour d'un objet.
facile aussi quand on veux regarder devant soi même avec une trajectoire non linéaire ( il suffit que la mire ait la même trajectoire que la caméra mais un peu en avance )

pour la réactualisation , c'est bien la deuxième approche. ( celle que tu as prise )
il faut prendre un repère global fixe dans lequel le paysage est fixe , et la caméra + evt diff objets sont mobiles.
( pour plein de raisons diff à résumer )
donc réactualiser les projections de chaque polygone ( "coord sur l'écran" )à chaque image. Ce que tu dois faire de toute façon.
lourd ou pas. !?
le plus lourd dans ce type de soft , c'est le rendu quand tu rajoutes des sources de nature diverses, des textures, des ombres, etc.......
(voir bien plus complexe)
en espérant t'avoir répondu en partie.

[Dlzlogic]

Bonjour,
Ca fait plaisir de vous relire.
A mon avis, il y a deux options : soit votre image plastique est compliquée, c'est à dire qu'il y a beaucoup d'éléments. Alors, à mon avis la seule solution est de créer le film image par image, que vous stockez quelque par pour les visionner ensuite en continu.
Soit votre image plastique est simple, alors vous pouvez créer chaque image, par exemple 10 images par seconde, en temps réel. Concernant le traitement, c'est pareil, la seule différence est la gestion des résultats.

Bien-sûr, je pourrais vous détailler la façon dont j'ai procédé pour faire cela. J'ai utilisé beaucoup de papier et usé mes crayons. La difficulté n'est pas la programmation mais de savoir ce que l'on veut programmer. Dans tous les cas il faut procéder image par image. Suivant les temps d'exécution, on les stocke ou pas.

[Tryss2]

pour la réactualisation , c'est bien la deuxième approche. ( celle que tu as prise )
il faut prendre un repère global fixe dans lequel le paysage est fixe , et la caméra + evt diff objets sont mobiles.
( pour plein de raisons diff à résumer )

Ah, donc ceux qui ont développé OpenGL ont tout faux?

As far as OpenGL is concerned, there is no camera. More specifically, the camera is always located at the eye space coordinate (0., 0., 0.).

[ansset]

Tu ne cites que l'intro de l'article, pas la suite qui concerne les mouv de caméra!!!!
de toute façon, on peut ( et on doit ) faire une transformation matricielle dans un sens ou l'autre si la caméra bouge.
anyway, si on veut faire du mouvement , l'interface pour définir ce mouvement se fait à partir d'un mouv de caméra dans l'espace.

ps: à programmer c'est plus "intuitif" aussi. et je ne vois pas pourquoi ce serait plus lourd.

[ansset]

n'oublions pas que la question de base est de programmer "from scratch" un soft3D simple.

[Dlzlogic]

Un petit rajout concernant le système de référence.
Si l'image plastique observée est un paysage, alors ce paysage est connu dans son système de référence d'origine. La raison en est surtout que on ne voit qu'une partie, donc, ce serait idiot de faire un changement de référence sur l'ensemble. C'est la caméra qui bouge et le point visé. L'angle d'ouverture, c'est à dire la focale utilisée, est une convention, soit il est défini par la distance entre la caméra et le point visé, solution que j'ai adoptée, soit c'est défini autrement, alors le point visé n'est qu'une direction.
Autre hypothèse, l'objet observé n'a pas de verticale propre, alors, la caméra est fixe et c'est l'objet qui tourne sur lui-même, se rapproche ou s'éloigne..

[ansset]

n'oublions pas que la question de base est de programmer "from scratch" un soft3D simple.

puisqu' on a cité OpenGL, il faut savoir qu'il fait "le boulot' à ta place , en connexion avec une carte graphique compatible.
mais je pensais que "l'idée" de départ était un programme de base , totalement indépendant.

si praecilia le souhaite ; je peux en parler par MP .

[ansset]

question importante :
avec quel logiciel de programmation travailles tu ?

[Dlzlogic]

@ annset,
Je pense que précilla a été très clair. Il ne s'agit en aucun cas de faire une application qui remplacerait je ne sais quel logiciel existant, mais de faire l'applicatif lui même. Autrement dit, qu'importe l'efficacité, les performances, il s'agit tout simplement de le faire soi-même.
Ceci pour dire que toute référence à des choses existantes est sans objet. De même que la question "quel logiciel de programmation ?", d'autant que le terme plus approprié serait plutôt "quel langage de programmation ?". Par exemple on peut supposer que c'est C/C++ + QT, mais cela n'a aucune importance, considérant la formulation très précise et confirmée.
D'un autre côté, je suis bien d'accord qu'il y aura un moment où il faudra "voir" un résultat, mais actuellement, laissons précilla se poser et résoudre les bonnes questions.
Pour ma part, j'ai réfléchi très longtemps et beaucoup écrit (papier/crayon) avant de taper la moindre ligne de code.

@ précilla, un conseil, il faut toujours se ramener à des calculs en 2D, c'est à dire sur un plan. C'est là que Thalès est notre mathématicien préféré.

[ansset]

@ annset,
Je pense que précilla a été très clair. Il ne s'agit en aucun cas de faire une application qui remplacerait je ne sais quel logiciel existant, mais de faire l'applicatif lui même.

j'ai vu que tu faisais ref à cette discussion sur un autre fil.
et ce n'est pas mon interprétation de la question initiale.
alors je ré itère, OpenGL est un logiciel "bas-niveau" en direct avec la carte graphique.
et concernant Praesilia, mon interprétation était qu'elle voulait essayer d'écrire un logiciel à partir de rien.
(d'où ses premières questions sur la projection du rectangle.)
dans cet esprit prendre l'architecture logicielle d'OpenGL en ref pour ré écrire les fonctions de base en logiciel haut niveau me semble être à priori discutable.

[ansset]

à l'opposé, et si je te suis, autant prendre directement 3DSmax ou Maya par exemple , et écrire des plugs-in , non ?