Bonjour,
La dilatation du temps en relativité générale est régulièrement traitée à partir de la métrique de Schwarzschild, donc de la gravité. Pourtant les choses me semblent plus simples en utilisant à partir de la RR l'accélération "ordinaire" au lieu de celle de gravité, et le principe d'équivalence.
On part de l'invariant :
c².dτ² = c².dt² - v².dt²
(je n'explicite pas les termes, utilisant les conventions habituelles d'écriture).
Si v est variable et le mouvement uniformément accéléré,
v = γ.t d'où c².dτ² = c².dt² - γ².t².dt²
En divisant par c² : dτ² = dt² - (γ².t²/c²).dt² soit
(1) dτ² = (1 - γ².t²/c²).dt²
Le mouvement étant uniformément accéléré, d=1/2.γ.t² donc γ.t² = 2.d soit
γ².t² = 2.γ.d
Dans γ.d on reconnait le potentiel gravitationnel Φ, d'où
γ².t² = 2.Φ
En reportant dans l'équation (1) : dτ² = (1 - 2.Φ/c²).dt² soit
dτ = √(1 - 2.Φ/c²).dt
Au signe près, on reconnait la formule de dilatation du temps dans la métrique de Schwarzschild, le "-" ici étant dû au fait qu'on a supposé l'accélération dans le sens des x alors que dans la métrique de Schwarzschild, l'axe des x est dirigé vers l'extérieur de la masse sphérique tandis que g pointe vers la masse.
Ma méthode est-elle légitime ?
Merci
-----




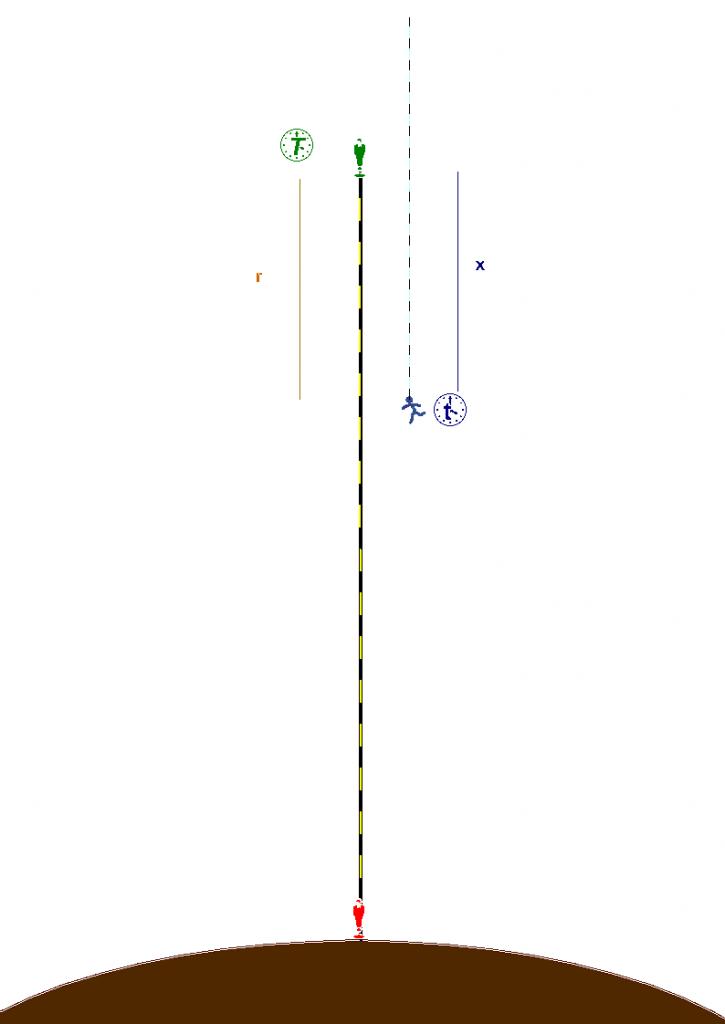
 ( Vert) et
( Vert) et