Bonjour à tous,
Je me pose la question suivante : Comment s'exprime le temps sur un cercle situé à un rayon R1 du centre d'une galaxie, par rapport au temps situé sur un cercle de rayon R2, tel que le prédit la Relativité Générale ? Voici une image :
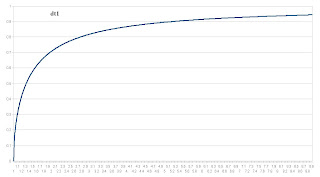
Pouvons nous dire selon ce qui est décrit ici, que R2 étant >> R1 (très loin du centre), alors dt1 = racine (1-rs/r1) dt2 ?
Donnant cette courbe pour dt1 en fonction de r1 :
Dernière modification par Galuel ; 22/11/2009 à 10h21.
Bonjour,
Dans ton dessin les 2 cercles ne subissent pas les effets gravitationels de la même masse (il s'agit grosso modo de la quantité de matière de à l'intérieur des cercles).
De ce fait la valeur du rayon de schwarzschild n'est pas utilisable directement comme ça. Il faut que le rapport des masses apparaisse.
De plus, les effets gravitationnels dans un objet peu homogène tel que notre galaxie n'est pas si simple. Ce que je veux dire c'est que depuis la surface de la Terre, l'effet gravitationnel qui domine n'est pas la galaxie, ni même le Soleil mais la Terre. Donc la comparaison de la différentielle de Temps dépends en réalité plus de l'objet le plus proche de ton observateur dans ce cas.
Mainteant si tu let deux observateurs sur de des cercles plus grands que la galaxie ton expression peut s'appliquer
Comment traiter le problème au sein de la galaxie en connaissant la répartition de sa masse supposée homogène sur un cercle r : M(r) ?Envoyé par physeb
Il afut justement que tu exprime ta métrique de Schwarzshild avec 'm' la masse contenu dans le cercle de rayon r.
Ton rayon de Schwarzschild (rs) s'exprime en fonction de cette masse.
Donc si tu n'a pas les mêmes masses à l'intérieur de tes cercles tu ne peut avoir le même rs.
Il faut exprimer les deux métriques puis les comparer.
Certes, mais donc je dois avoir une idée de M(r) pour une galaxie, et même peut-être pour l'histoire d'une galaxie une idée de M(r,t), avons nous ce genre d'information ?
Le ralentissement temporel dépend du ratio entre le rayon de Schwarzschild et le rayon de la masse.
Avec Rs le rayon de Schwarzschild et r le rayon de la région considérée.
Soit une masse galactique de disons 400 GMo.
Rs = 2GM/c2 ~ 1015m
r ~ 35 000 al soit ~ 3.1020 m.
Soit un ratio t/tau qui ne diffère de 1 qu'à la 6e décimale.
a+
Parcours Etranges
Imaginons un disque (les galaxies sont planes, comme les systèmes stellaires, à peu de choses près...)...
Je peux supposer que la masse se répartit sur le disque selon : M(r) = M0 x pi r²
Rs = 2G M0 pi r² / c2, donc Rs / r est proportionnel à r
Et donc dt1 = racine (1-r/r0) dt2 avec r <= r0, r0 étant donc la distance de l'observateur lointain où dt1 = dt2.
Correct ?
Je corrige :
Imaginons un disque (les galaxies sont planes, comme les systèmes stellaires, à peu de choses près...)...
Je peux supposer que la masse se répartit sur le disque selon : M(r) = M0 x pi r²
Rs = 2G M0 pi r² / c2, donc Rs / r est proportionnel à r
Et donc dt1 = racine (1-r/r0) dt2 avec r <= r0, au sein du disque...
Puis au delà du disque on a tout le temps Rs = 2GM(du disque)/c2 = constante, et :
dt1 = racine (1-Rs/r) dt2
Juste ?
Si M0 est la masse de la galaxie et r0 son rayon alors ça serait plutôt :
M(r) = M0 x pi (r/r0)²
C'est 1/racine()dt1 = racine (1-Rs/r) dt2
Mais sinon tu as vu qu'à la base, le calcul d'ordre de grandeur montre qu'il n'y a pas de différence de temps propre significative entre les différentes région d'une galaxie (disque, bulbe...), sauf bien sûr très localement, au voisinage immédiat des astres compacts (naine blanche, étoile à neutron, trou noir), je ne vois pas trop où tu veux en venir, j'avoue.
a+
Parcours Etranges
Oui certes...
Ben ça dépend de quel observateur on parle ! En l'occurrence ce qui m'intéresse ici n'est pas la valeur du temps quand on s'éloigne de la galaxie par rapport à un observateur près du centre, mais l'inverse, je prends pour référence un observateur très lointain, et je m'en rapproche (voir l'image avec les cercles).
C'est donc racine et pas 1/racine
Significative par rapport à quel type de phénomène, et selon quelle échelle spatio temporelle ? Je crois qu'on ne peut pas dire que ce soit n'est pas significatif si on ne précise pas exactement ce sur quoi on veut faire porter du sens. Pour l'instant je m'intéresse juste à ne pas faire d'erreur sur les sphères temporelles liées à une galaxie, par rapport à un observateur lointain, pas à leur signification.
Je résume donc étant donné M0,r0 le disque de matière on a :
r<r0 : dt1 = racine (1-r/Rs0) dt2
r>r0 : dt1 = racine (1-Rs0/r) dt2
Avec Rs0 = 2G M0 pi / c²
C'est correct ?
Je corrige (décidément ! :=) )
Je résume donc étant donné M0,r0 le disque de matière on a :
r<r0 : dt1 = racine (1-r.Rs0/r0²) dt2
r>r0 : dt1 = racine (1-Rs0/r) dt2
Avec Rs0 = 2G M0 pi / c²
C'est correct ?
Me suis encore fourvoyé M(r) = M0.r²/r0², il n'y a pas de "pi", n'est-ce pas (comme quoi tout le monde peut se tromper).
Je résume final :
(r<r0) dt1 = racine (1-r.Rs0/r0²).dt2 et (r>r0) dt1 = racine (1-Rs0/r).dt2
Ca donne donc cela.
Voici la suite des courbes retraçant les sphères temporelles lors de l'histoire de l'effondrement du disque, par rapport à un observateur se tenant à 20 rayons de Schwarzchild d'un disque de matière initial d'un rayon de 12 Rs.... Au delà de r0 les courbes se rejoignent toutes, ce qui est normal...
Dans le cas d'une boule la masse homogène s'écrit : M(r) = M0.r^3/r0^3, c'est la seule chose qui change ! Et donc tout simplement on a :
(r<r0) dt1 = racine (1-r2.Rs0/r0^3).dt2
(r>r0) dt1 = racine (1-Rs0/r).dt2
La seule chose qui change vraiment c'est donc à l'intérieur de la boule de matière où le facteur r2/ro^3 remplace r/r0^2, ce qui donne pour l'histoire de l'effondrement de la boule ceci pour les sphères temporelles :
C'est quoi une boule qui s'effondre comme ça ? C'est simplement une étoile qui se transforme en trou noir (si elle passe sous Rs0 en rayon, elle devient trou noir)...
Je me trompe jusqu'à présent ou pas ?
