Résouble problème à n corps avec Newton

[invite5c1d24aa]

Bonjour à tous,
J'ai réaliser un algorithme pour simuler le problème à n corps à partir de la loi de Newton F=GMm/d².
J'utilise MathCad Prime.
Le principe est simple:
pour chaque corps "i" je calcule les vecteurs déplacements générés par les autres corps "j".
Dans le cas ou i=j le vecteur déplacement est celui causé par la vitesse propre du corps.
Pour chaque "i" Je somme les vecteurs "j" et j'obtiens le vecteur résultant.
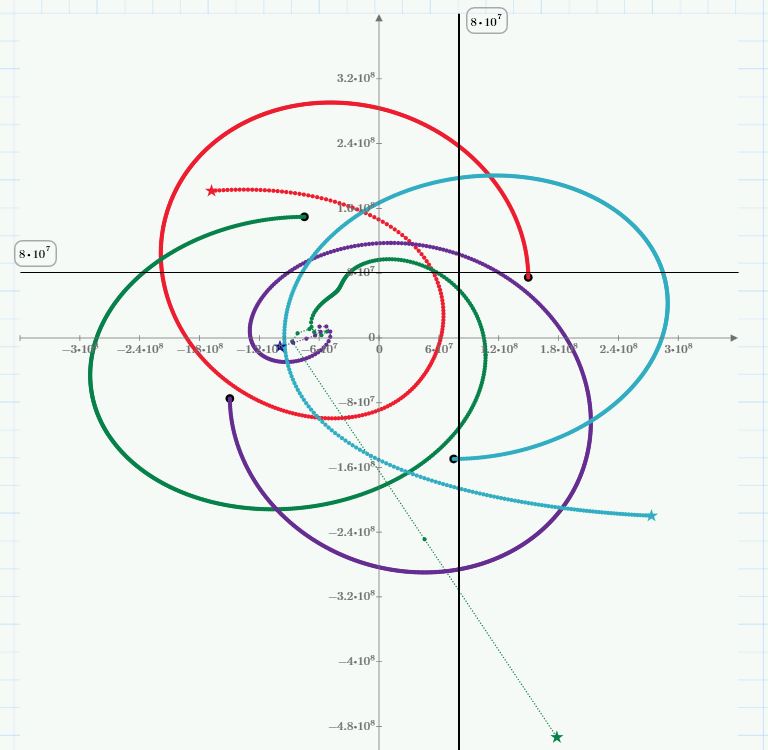
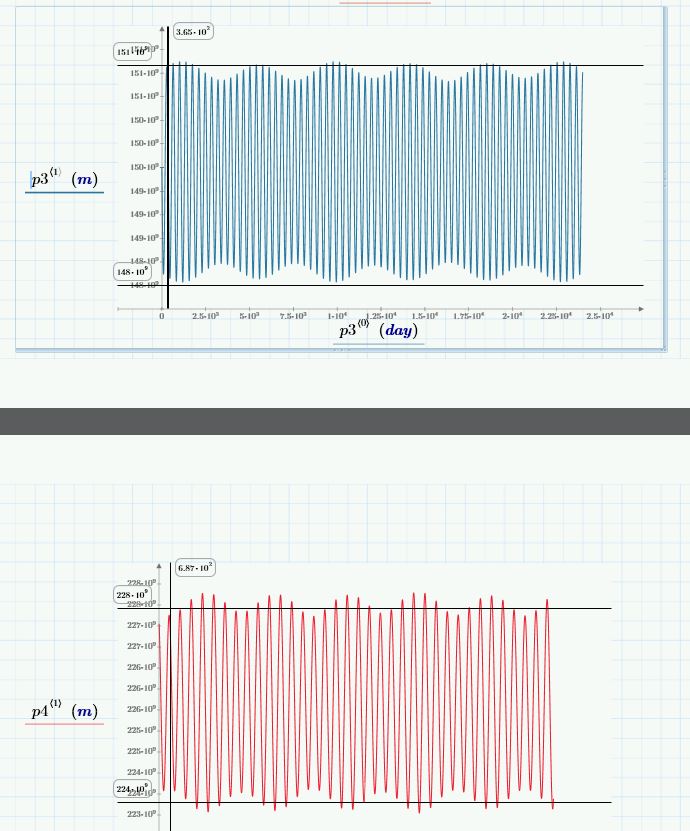
Pour le système solaire les résultats (grand axe, petit axe, excentricité, vitesses ...) sont convaincants.
Mais ... j'ai constaté que le soleil se déplaçait sans jamais revenir à sa position initiale !
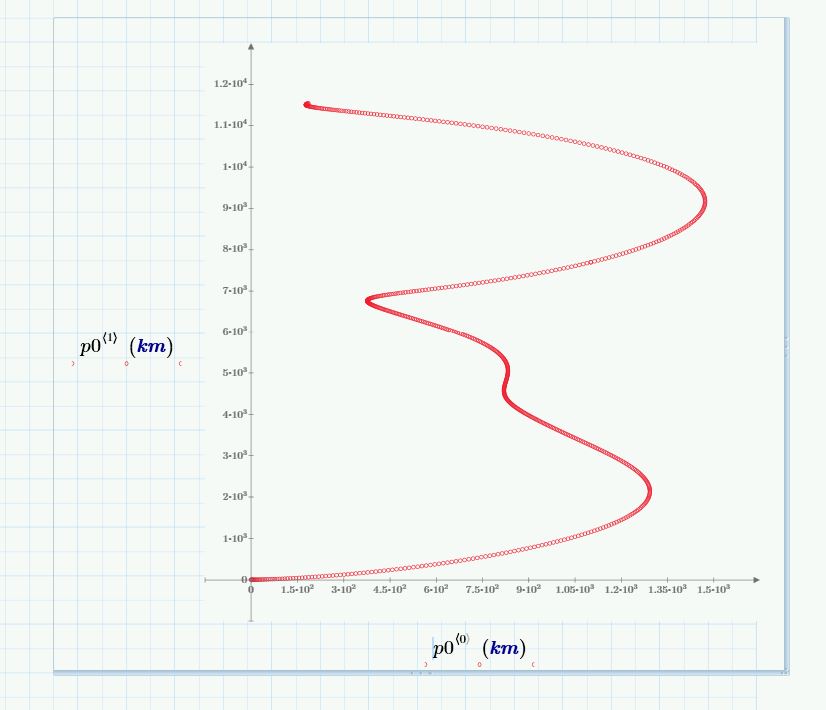
J'ai dons réalisé la simulation avec le système Terre-Lune (au départ la Terre a une vitesse nulle.
Et la surprise: la Terre se déplace sur l'axe des "y" à raison de 30.000Km par révolution lunaire sans jamais revenir à son point de départ.
La logique voudrait que la Terre effectue un "8" pour revenir à sa place initiale.

Qu'en pensez vous ?
Merci de m'apporter un éclairage nouveau.

Cordialement.

PS je peut poster la programmation MathCad Prime si Vous le souhaté.
-----

[phys4]

Bonjour,
S'il n'y a pas d'erreur de programmation , la vitesse globale non nulle peut provenir des conditions initiales : si l'ensemble des vitesse initiales du modèle ne correspondent pas à un barycentre immobile, il y aura un déplacement d'ensemble à chaque période du mouvement.

[invite82078308]

Difficile de répondre à priori, toutefois, je soupçonnerais l'impact d'erreurs d'arrondi cumulées.
Voir cependant d'abord comme le soupçonne phys4, si un référentiel adéquat (centré sur le barycentre du système) ne permet pas de régler le problème.

[phys4]

Par exemple :

J'ai dons réalisé la simulation avec le système Terre-Lune (au départ la Terre a une vitesse nulle.
Et la surprise: la Terre se déplace sur l'axe des "y" à raison de 30.000Km par révolution lunaire sans jamais revenir à son point de départ.
La logique voudrait que la Terre effectue un "8" pour revenir à sa place initiale.

La vitesse initiale de la Terre ne doit pas être nulle mais opposée à celle de le Lune et dans le rapport des masses.

La logique veut que les deux corps tracent des ellipses homothétiques.

[A voir en vidéo sur Futura]

[invite5c1d24aa]

Bonjour à tous et merci pour vos réponses.

La remarque de Schrodies-Cat concernant la précision des calculs n'est pas fondée. J'utilise un logiciel de math et par exemple je trouve pour l'excentricité de la Terre 0.01699022 contre 0,016710220 dans une revue.

La première remarque de Phys4 concernant le référentiel est intéressante mais la deuxième est moins pertinente car pourquoi devrait-on modifier les conditions initiales d'un des corps ?

Je me suis donc concentré sur le changement de référentiel.
Donc pour le Soleil J'ai remplacé les coordonnées absolues en coordonnées différentielle.
Et voilà ce que j'obtient pour le système Soleil-Terre-Mars.
TrajSoleilTM.JPG
et pour le système Soleil-Mercure-Vénus-Terre-Mars
TrajSoleilMVTM.JPG

[mach3]

La première remarque de Phys4 concernant le référentiel est intéressante mais la deuxième est moins pertinente car pourquoi devrait-on modifier les conditions initiales d'un des corps ?

si vous voulez que votre système dans son ensemble ne se déplace pas (c'est à dire que le barycentre soit immobile et que le soleil reste confiné au centre même si il bouge un peu), vous devez avoir :



et vous pouvez ajouter :



si vous voulez que le barycentre soit à l'origine.

Cela contraint vos conditions initiales. Si vous avez n astres, vous avez 2n vecteurs à spécifier comme conditions initiales (positions et vitesses). Si vous imposez que l'ensemble ne se déplace pas, l'une des n vitesses dépend des n-1 autres, vous n'avez plus que 2n-1 paramètres libres pour vos conditions initiales. Vous arrivez à 2n-2 si en plus vous voulez que le centre de masse soit à l'origine.

Vérifiez que vos conditions initiales respectent bien la première contrainte. Si elle n'est pas respectée, alors l'ensemble de votre système possède une quantité de mouvement et se déplace donc en ligne droite.

m@ch3

[invite5c1d24aa]

Merci mach3 pour ce développement très clair.
Effectivement dans ce cas le barycentre "Soleil" ne bouge pas.
Mais je ne souhaite pas imposer cette contrainte.
Je souhaite reproduire ce qui se passe réellement.
Et voila ce que j'obtiens : déplacement de la Terre dans le système Terre-Lune en 29 Jours
TrajTerreLabs.JPG
Et voila ce que j'obtiens : déplacement du Soleil dans le système Soleil-Mercure-Vénus-Terre-Mars en 730 Jours
TrajSoleilMVTMabs.JPG

Donc selon vos dire, cela est réel.

[mach3]

Mais je ne souhaite pas imposer cette contrainte.
Je souhaite reproduire ce qui se passe réellement.

ça n'a rien à voir avec réel ou non réel, c'est simplement un choix de référentiel, dans l'un le barycentre bouge, dans l'autre il ne bouge pas et il n'y a pas un point de vue plus réel qu'un autre.
vous pouvez très bien spécifier les 2n conditions initiales (alors votre barycentre bougera en mouvement rectiligne uniforme), puis ensuite changer de référentiel pour que le barycentre ne bouge pas, voir même de coordonnées pour que ce barycentre soit à l'origine, ce faisant vous décalerez vos conditions initiales (application de transformation de Galilée et de transformation affine) et implicitement ce sera comme-ci vous n'aviez spécifié que 2n-1 ou 2n-2 condition initiale (l'autre ou les deux autres se déduisant seules). Ça ne change rien et il n'y a pas une approche plus "réelle" qu'une autre.

m@ch3

[invite5c1d24aa]

Je vois.
Tout est question de point de vue comme l'avait prédit Einstein.
Merci pour cet éclairage.

[Gilgamesh]

Je vois.
Tout est question de point de vue comme l'avait prédit Einstein.

Rendons à César...

La relativité qui s'applique ici est celle de Galilée ("le mouvement est comme rien").

[invitedd63ac7a]

Mais ... j'ai constaté que le soleil se déplaçait sans jamais revenir à sa position initiale !

Comment le logiciel calcule-t-il les déplacements des corps sous l'influence de la gravité des autres. Je suppose qu'il y a une intégration numérique des trajectoires, quelle est la méthode utilisée ?

[invite5c1d24aa]

Voila l'algorithme

Il y a n corps de coordonnée M(x,y), de Masse K, vitesse v, angle du vecteur vitesse α.
En 2 dimensions. Soleil coordonnée (0,0) vitesse= 0
Pour chaque seconde
Pour chaque corps i0 de 1 à n
Pour chaque corps i de 1 à n
Si i = i0 (interaction du corps avec lui-même)
Calcul du déplacement d du corps Ci à partir vecteur vi
Calcul des Δ des coordonnées Mi à partir de d ; α i.
Sinon
Calcul de la distance d entre Ci et Ci0
Calcul de l’angle θ = atan(Δy / Δx) entre d et l’abscisse
Calcul de l’accélération subit par Ci = G.Ki0 / d2 = γ
Calcul du déplacement d du corps Ci = γ .t2
Calcul des Δ des coordonnées Mi à partir de d ; θ.
Fin boucle corps i
Calcul des nouveaux paramètres de Mi
Δx = ∑ Δxi0 Δy =∑ Δyi0
vi = √∆2x + ∆2y
Mx i = Mx i + Δx
My i = My i + Δy
α i = atan(Δy / Δx) ajustement en fonction signe des Δ
Fin boucle corps i0
Stockage coordonnée Mn(x,y)
Fin boucle temps

Les orbites des planètes sont bien des ellipses.
Et le soleil se déplace comme ci-dessous
Conditions initiales: Soleil, Mercure, Vénus, Terre, Mars alignés sur l'axe des X.
Durée 700 jours ( > révolution de Mars)

[phys4]

Les orbites des planètes sont bien des ellipses.
Et le soleil se déplace comme ci-dessous
Conditions initiales: Soleil, Mercure, Vénus, Terre, Mars alignés sur l'axe des X.
Durée 700 jours ( > révolution de Mars)

Très joli résultat, vous devriez constater qu'avec ces données initiales, les orbites des planètes se déplacent avec le même écart que le Soleil.
La vérification précise ne peut sans doute se faire que sur plusieurs orbites.

C'est l'alignement des planètes en x, qui crée le départ rapide du Soleil vers les x, puis son entrainement en y.

[invite5c1d24aa]

Discussion très enrichissante.
Exemple illustré : système Terre Lune (calcul plus rapide)
effectivement dans le cas d'une Terre "mobile" le système se déplace par sauts de puce (parabole couchée)
TerreLuneDyn.JPG
si la Terre reste immobile le système ne se déplace pas.
l'orbite elliptique de la Lune est illustré par un tracé montrant la variation du rayon en fonction du temps
TerreLuneSta.JPG
et pour le fun voici un ballet de 4 Soleils à 30km/s distant d'une ua durée 200 jours
4Etoile2_a_200.JPG
merci à tous

[phys4]

Le ballet des 4 "Soleils" est surement instable et devrait se finir de façon cataclysmique, il me semble qu'il y a un point de quasi collision sur le graphique.

Le système Terre Lune est typique, une belle cycloïde pour la trajectoire de le Terre avec ces conditions initiales.

[Calvert]

il me semble qu'il y a un point de quasi collision sur le graphique.

Oui, cela doit d'ailleurs poser des problèmes numériques. Un bon test pour ce genre de simulation est de vérifier que l'énergie totale est bien conservée au cours du temps.

[invite5c1d24aa]

J'ai intégré une détection de collisions, mais sur ce modèle il n'y en a pas.
Les croisements existent bien mais pas de collision !
J'ai même poussé la simulation à 500 jours (4 heures au moins de calcul !) mais pas de collisions
Tracé à 500 jours .. flèche bleu = points de départs, flèches vertes =point d'arrivées.

[Calvert]

Oui, mais le brusque changement de direction du corps violet (celui du bas), montre qu'il est passé très près d'un autre corps. Dans ce cas, il est possible (probable si tu as un point à chaque pas de temps), que ton pas de temps devienne trop grand dans cette configuration. Il faut adapter le pas de temps pour s'assurer que les vitesse ne "changent pas trop" d'un pas de temps au suivant.

[invite5c1d24aa]

Sur le tracé, le pas de temps est de 1 jour mais dans le calcul le pas de temps est de une seconde !
C'est pour cette raison que le calcul est très long : plus de 4 heures pour le "ballet des Soleil".

[Calvert]

Sur le tracé, le pas de temps est de 1 jour mais dans le calcul le pas de temps est de une seconde !

Ah oui, d'accord !

Du coup, c'est un aspect de ton code qui peut sans doute être optimisé : il n'est peut-être pas utile d'avoir tout le temps un pas de temps aussi court.

[invite5c1d24aa]

Merci Calvert pour la suggestion.
J'ai maintenant un pas d'un jour, que je peux modifier.
Mon module de détection de collision a du être sérieusement revu et corrigé !
Voila ce que cela donne avec ces nouveautés.
Configuration initiales légèrement différentes et durée de 618 jours et une collision détectée une!
On en profite pour percevoir l'effet de l'accélération gravitationnelle avant la collision courbe verte.

[Calvert]

J'ai maintenant un pas d'un jour, que je peux modifier.

Les collisions sont un sérieux problème, de même que les passages rapprochés. Comment gère tu ton pas de temps ? Idéalement, il faudrait t'assurer que la vitesse ne change "pas trop" pendant un pas de temps (ce qui peut devenir très faux dès que tes objets sont très proches). Pour chaque corps, il faudrait tester la vitesse avant-après, et définir une contrainte (par exemple, le module de la vitesse ne doit pas changer de plus de n% pendant un pas de temps, et l'angle de m radians). Si cette contrainte n'est pas respectée, revenir au pas de temps précédent, et utiliser un pas de temps plus petit.

Ceci évite des comportement bizarres lors des passages rapprochés.

De même, tu peux faire en sorte que ton code augmente le pas de temps lorsque les vitesses changent très peu.

Mais c'est un gros travail. Les codes à "n-corps" pro utilisent des pas de temps différents pour chaque corps pour optimiser le temps de calcul.

PS: mais bravo pour le travail ! C'est déjà remarquable !

[invite5c1d24aa]

En fait, à l'origine je souhaitais modéliser le système solaire avec la seule loi de Newton.
Et constater que cette seule équation permet de modéliser le cosmos est fascinant.
Le fait de passer d'un pas d'une seconde à un jour me permet de modéliser l'ensemble du système en un temps record.
Le pas est modifiable au début du programme et c'est tout.
L'idée du ballet des étoiles avec (ou sans collisions) est venus après pour conforter le génie de Newton et pour la beauté du tracé.
Pour info, le programme de calcul des trajectoires tient sur 2 pages.
Le programme de calcul de détection de collision prend lui 2 pages également!
En fait le principe est le suivant :
il faut avoir les coordonnées spatiales des 2 corps c1 et C2 à analyser à l'instant t et t1=t+pas
trouver les paramètres a et b de l'équation affine f(x)=ax + b correspondant à la trajectoire (supposée rectiligne pendant le pas de temps) du corps c1
trouver les paramètres a' et b' de l'équation affine g(x)=a'x + b' correspondant à la trajectoire (supposée rectiligne ...) du corps c2
résoudre le système d'équation
s'il y a une solution (intersection), vérifier que ces coordonnées appartiennent à [c1] et [c2] dans l'espace de temps t,t1.
et le corps qui a l'énergie cinétique la plus élevée absorbe l'autre.
Pour l'instant ca s'arrête là.
il n'y a pas de gestion de choc avec les conséquences sur la trajectoire.
mais ca va venir !

ci-dessous , tracé montrant la variation du rayon de la Terre (bleu) et Mars (en rouge) autour du soleil (fixe)
avec la présence jupiter et saturne
le calcul s'étale sur 60 ans (période nécessaire pour que les planètes se retrouvent à leur point de départ avec un pas de 1 jour (25000 itérations)

on remarque que les trajectoires ne sont pas des ellipse pures mais avec quelques "ondulations" (duent à la présence de jupiter et saturne) dans la variation du rayon.