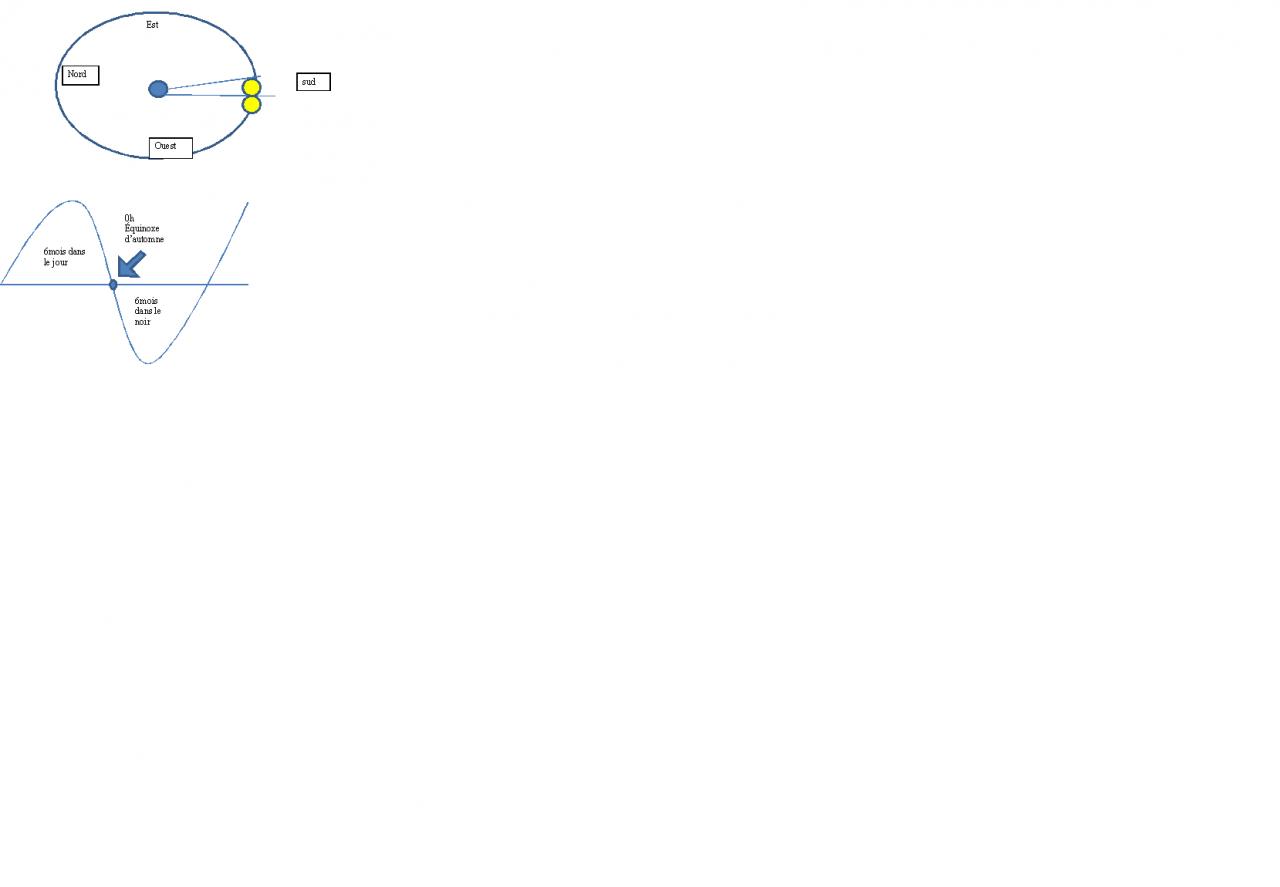Trouver la distance terre-lune ? Trouve le temps du coucher de soleil ?

[invite77165402]

Bonjour,

j'ai un devoir d'astrophysique à remettre et j'ai quelques problèmes...

Voici la première question :

Ptolémé à mesuré la distance Terre-Lune en terme du diamètre de la Terre. Pour ce faire, il a observé un angle
de 44.05◦ entre la Lune et les étoiles au zénith. Il savait que 3 heures plus tôt, la Lune était elle-même au zénith.
Dans son calcul, il tient compte de la révolution de la Lune autour de la Terre (et ignore le mouvement de la Terre
autour du Soleil). Retrouvez la mesure de la distance Terre-Lune de Ptolémé (par rapport au diamètre de la Terre)
en utilisant ses observations.

j'ai fait un triangle rectangle dans lequel j'ai trouvé un autre angle de 44.95. J'ai pris le rayon de la terre qui vaut 6371km...

Ensuite je me suis dit que la période sidérale (temps que la une doit parcourir pour revenir dans la même configuration p/r aux astres),
soit le temps(donc 27.5j) qu’elle prend pour faire le tour de la terre(soit 360°) était égal au rapport de trois suivant :

27,3j/ 360° = 3h/X
Conversion jour en heure:
27j = 655,2h
Règle de trois pour trouver la valeur de l’angle p/r au centre de la terre:
360° X 3h / 655,2h = x
x =1,648°.

Ensuite on pourrait utiliser la règle des sinus pour un triangle quelconque :
A/ sinA = B/SinB = C/sinC
6371/Sin? = ?/sin1,648 = C/sin135.95°

...Bref je galère...


Ensuite deuxième question :


Le jour solaire est défini par le temps que met le Soleil pour revenir au même endroit dans le ciel. Appelons ce jour
solaire “le vrai jour solaire” (soit 24 heures sur nos montres). (b) Dans ce nouveau système, avec la révolution terrestre inversée et plus rapide, calculez la durée
du coucher du Soleil (soit le temps entre le moment où le Soleil touche l’horizon et le moment où il disparaît sous l’horizon) pour quelqu’un qui
habite à une latitude de 90◦ sud. (c) Quelle est la durée de ce même coucher de Soleil pour quelqu’un qui le voit de
l’´equateur? (N´égligez l’effet de la réfraction atmosphérique.)

Quelqu'un aurait un éclair de génie SVP ?


Merci!
-----

[phys4]

Bonsoir,
je vous laisse pour la première question qui utilise la parallaxe terrestre pour trouver la distance Terre-Lune, il faut utiliser une période orbitale lunaire très précise pour avoir un résultat approché.

Le jour solaire est défini par le temps que met le Soleil pour revenir au même endroit dans le ciel. Appelons ce jour
solaire “le vrai jour solaire” (soit 24 heures sur nos montres). (b) Dans ce nouveau système, avec la révolution terrestre inversée et plus rapide, calculez la durée
du coucher du Soleil (soit le temps entre le moment où le Soleil touche l’horizon et le moment où il disparaît sous l’horizon) pour quelqu’un qui
habite à une latitude de 90◦ sud. (c) Quelle est la durée de ce même coucher de Soleil pour quelqu’un qui le voit de
l’´equateur? (N´égligez l’effet de la réfraction atmosphérique.)

Pour cette question , la personne qui se trouve à l'équateur voit le soleil se coucher à cause de la rotation de la Terre : donc rotation de 360° pour 24 heures, 15° par heure, 15' par minute donc environ 2 minutes pour le coucher, je vous laisse affiner avec vos données.
Au pôle Sud, seul la rotation autour du Soleil intervient, donc après un petit calcul vous devez trouver une variation de déclinaison de 1' par heure, soit quelques 30 heures pour 30'
Pour affiner le calcul, pensez à utiliser la variation sinusoïdale de déclinaison dont l'amplitude vaut 23°...

[invite77165402]

Je comprends que l'observateur bouge de 45° pendant les trois heures. Je peux faire le dessin de la parallaxe lunaire si je considère un observateur qui regarde le soleil p/r aux étoiles qui sont au zénith et l'observateur qui regardait la lune 3h plus tôt quand celle-ci était au zénith. Ce que je ne comprends c'est comment trouvé l'angle pour la lune. Si je fais mon rapport de trois 360X3h/655.2h = 1.648°, je ne comprends pas comment placer cet angle dans mon dessin. Aussi, normalement je devrais avoir besoin de la latitude de mon observateur, bref je ne sais pas comment positionner l'observateur sur la terre, je n'ai pas cet angle. Je sais qu'il est important de faire un dessin représentatif, je crois que j'ai la solution, mais il me manque beaucoup d'information pour trouver cette fichue distance!

Je sais que :

On est la nuit;
À l'époque de Ptolémé, donc procédé par triangulation;
J'ai 44.05 ° entre la lune et mes étoiles au zénith;
La lune était elle-même au zénith trois heures plus tôt
Ptolémé connaissait le rayon terrestre: 6371km
L'observateur a bougé de 45° en trois heures.
Angle de la Lune trouvé à l'aide de la période sidérale lunaire :~ 1.648°


....Est-ce que vous pourriez me dire comment utiliser mon angle lunaire de 1.648°et comment serait votre représentation graphique.

Merci!!

[Resartus]

Il y a trois angles à prendre en compte : l'angle de 1,648 que vous avez calculé, celui de 0.95° (45°-44,05°) et la différence entre les deux soit 0,698
Le décalage de 0,95 vient de deux facteurs qui se soustraient : l'effet dû à la rotation de la lune que vous avez calculé (1,648) moins l'effet dû à la rotation de la terre.
La terre a tourné de seulement 45° en 3 heures d'où un décalage à l'équateur de R.racine(2)/2 par rapport à l'axe entre la terre et la lune. il faut multiplier par cos(lat) si ptolémée avait fait sa mesure à une latitude différente .
L'angle dû à cette rotation vaut environ Rt*cos(lat)*racine(2)/2/Dtl (en radians)
La latitude est-elle fournie dans l'exercice? Mais si l'exercice parle de zenith cela veut dire que Ptolémée était à l'équateur.

Pour la représentation, il me semble qu'on peut mettre la situation alignée de la lune, de la terre et de l'observateur au zenith, et représenter la position 3 heures avant de l'observateur sur la terre et de la lune sur son orbite. Par contre, les angles ne se soustraient pas directement. Il faudra tracer des parallèles passant par l'observateur (angles alternes internes)

On pourrait être plus précis en prenant en compte le jour sidéral de la terre (3h fait un peu moins de 45°) et la distance observateur lune moins grande que centre de la terre lune. Mais je ne crois pas que ce soit nécessaire

[A voir en vidéo sur Futura]

[invite77165402]

Bonjour,

en ce qui concerne cette question:

Le jour solaire est défini par le temps que met le Soleil pour revenir au même endroit dans le ciel. Appelons ce jour
solaire “le vrai jour solaire” (soit 24 heures sur nos montres). (b) Dans ce nouveau système, avec la révolution terrestre inversée et plus rapide, calculez la durée
du coucher du Soleil (soit le temps entre le moment où le Soleil touche l’horizon et le moment où il disparaît sous l’horizon) pour quelqu’un qui
habite à une latitude de 90◦ sud. (c) Quelle est la durée de ce même coucher de Soleil pour quelqu’un qui le voit de
l’équateur? (Négligez l’effet de la réfraction atmosphérique.)

je ne suis toujours pas arrivé à la réponse...

Voici mon raisonnement:

Dans le cas de b) je suppose que, comme il s'agit du pôle sud, pendant 6 mois il fait jour et pendant le reste de l'année il fait noir. Donc, il y a un seul moment où il y a un coucher de soleil soit à l’équinoxe d'automne. Ci-joint le schéma très grossier de mon raisonnement(question 2 pour le dessin). En fait, mon problème c'est que je ne sais pas comment trouver mes dimensions dans le cas où je résous ce problème avec la trigo... bref, est-ce que je devrais passer par la trigonométrie, où une formule existe déjà? Pardonnez-moi Phys4, je n'ai pas compris pourquoi vous aviez trouver 2 mins. Je comprends que pour 24 on fait 360° 360/24h = 15°/h ou
15°/60min = 0.25°/min (ou 15'), mais pour le 2min à l'équateur... je ne suis pas capable de l'expliquer. Je ne comprends pas à quel moment je peux calculer le coucher...quel est le point de référence pour le calcul? Je suis complètement mêlé!

Merci de me répondre!!

[invite77165402]

voici ma représentation

[Lansberg]

Bonjour,

quels sont vos supports de cours pour répondre aux questions ???

Concernant la durée du coucher du soleil aux pôles, Phys4 a déjà donné des informations : cette durée dépend de la variation de la déclinaison du soleil, la rotation de la Terre sur elle-même n'intervenant pas.
La variation de la déclinaison du Soleil peut en première approximation être assimilée à une sinusoïde sur l'année. L'étude d'une sinusoïde peut donc apporter la réponse. Par exemple entre 5∏/6 et 7∏/6 on peut considérer que la variation de la déclinaison est linéaire. Il suffit alors de déterminer la durée qui sépare ces deux points ainsi que la variation de déclinaison.
À partir de là on peut calculer la variation de la déclinaison par jour ou par heure et ainsi calculer la durée du coucher du soleil (on trouve environ 31 heures, sans réfraction atmosphérique, ce qui est proche de ce donne l'imcce).

[invite77165402]

Le problème est résolu! Merci bcp!

[phys4]

Bonsoir,
Dans les exemples j'avais précisé qu'il vous appartenait de mettre les valeurs précises.

A titre d'exemple j'avais utilisé un diamètre apparent solaire de 30', alors que la valeur moyenne est de 32'.