Bonjour,
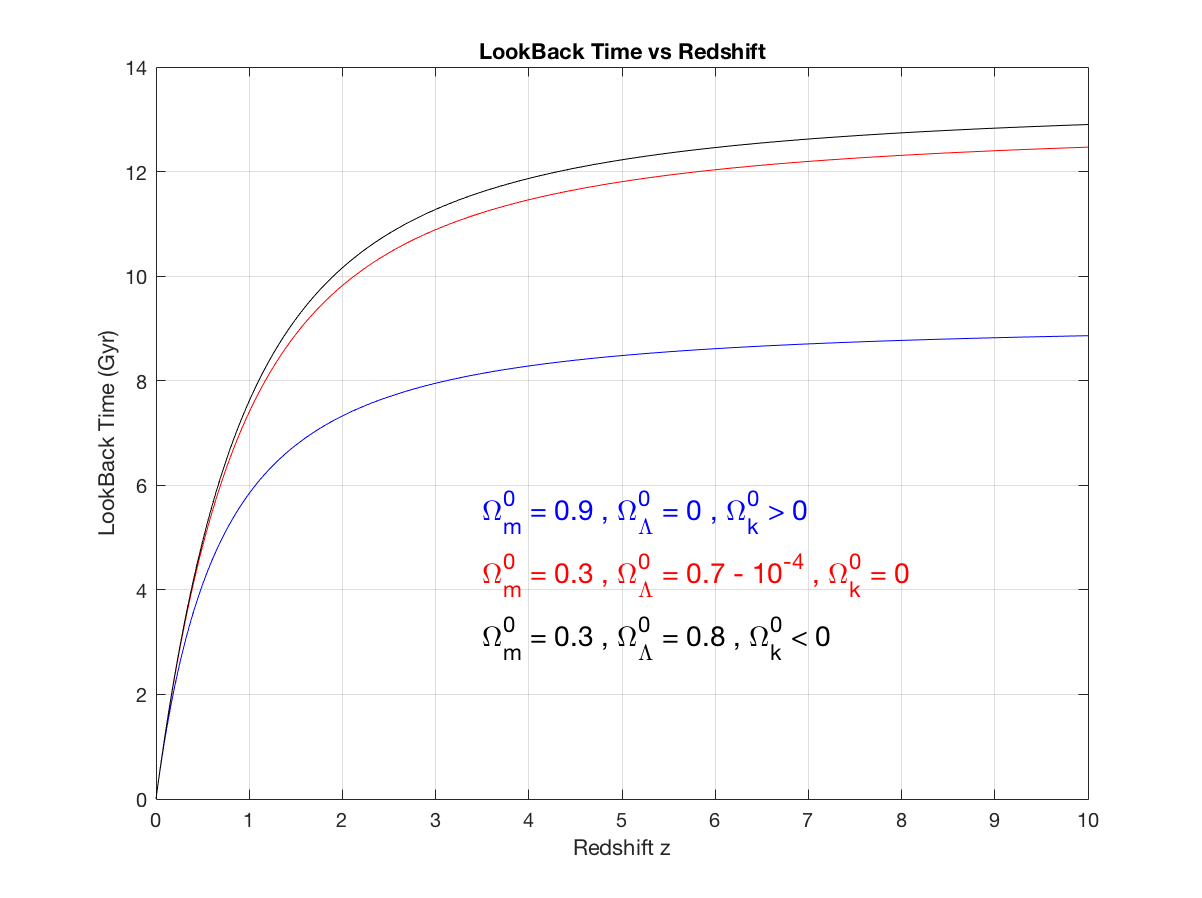
quand on parle de la distance d'une galaxie dans le langage courant, est-ce que ça correspond à la distance de la galaxie à l'époque où elle a émis le rayonnement que nous recevons actuellement ou à sa distance actuelle (autrement dit en tenant compte de la distance en + à cause de de la loi de Hubble) ?
Par exemple, pour la galaxie d'andromède, la distance évoquée est égale à 2.537 millions d'années lumière : nous la voyons donc telle qu'elle était il y a 2.537 millions d'années : ceci a-t-il un rapport avec une des 2 possibilités ci-dessus ?
Pour les petits redshift, je suppose que les 2 possibilités sont presque égales mais qu'en est-il pour des reshifts plus importants ?
Merci pour votre aide.
-----