Bonjour,
je m'exerce sur un exo de Physique Stellaire et notamment les questions ci-dessous :
1) Tout d'abord sur le profil de rotation pour la zone radiative : je sais que contrairement à la zone convective, où la rotation varie principalement en latitude (plus rapide à l’équateur qu’aux pôles), la zone radiative possède une rotation solide, c'est-à-dire qu'elle tourne d’un seul bloc.
Quel est donc la forme profil de rotation pour la zone radiative ?
Est-il plat, "képlérien" (je veux dire la vitesse est égale à), ou simplement circulaire (
et donc le profil serait linéairement croissant selon le rayon R) ?
2) Ensuite, quels processus physiques interviennent pour garder ce profil avec cette forme ?
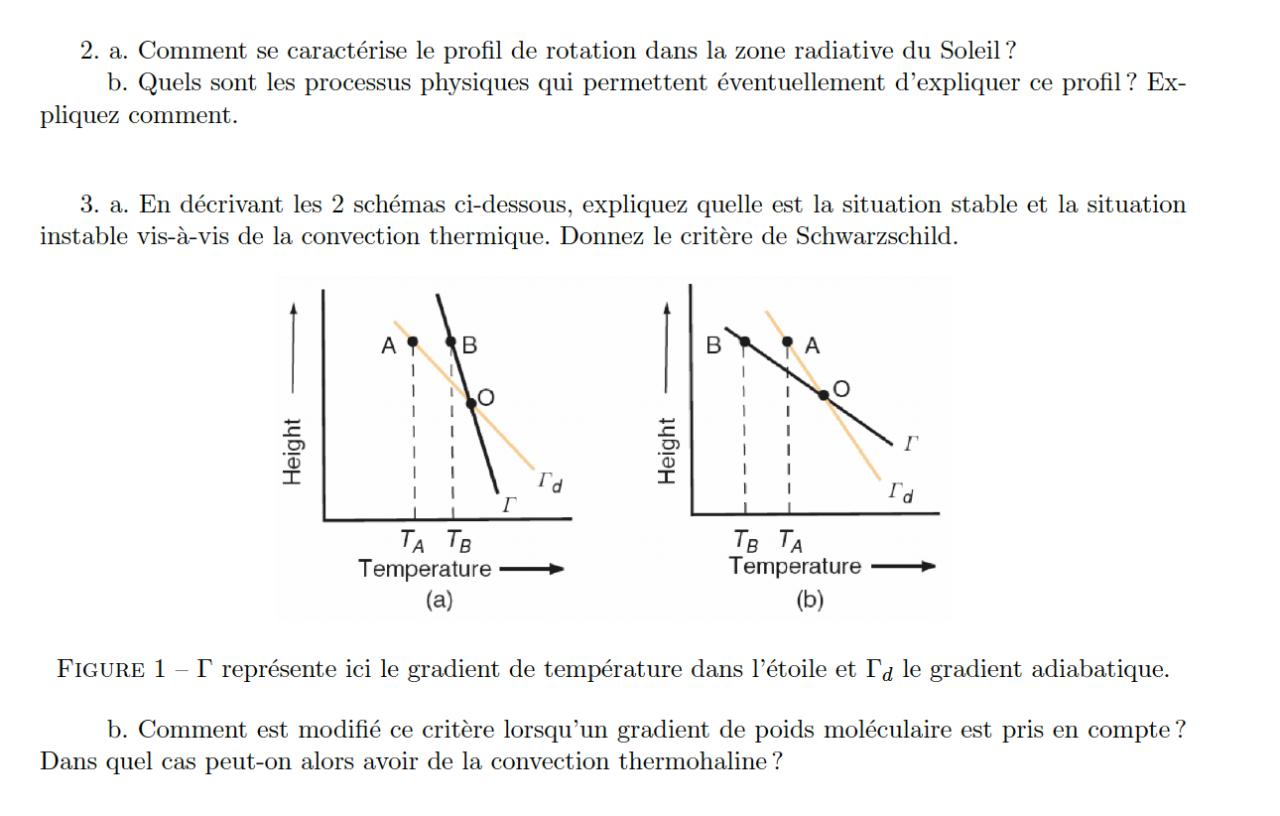
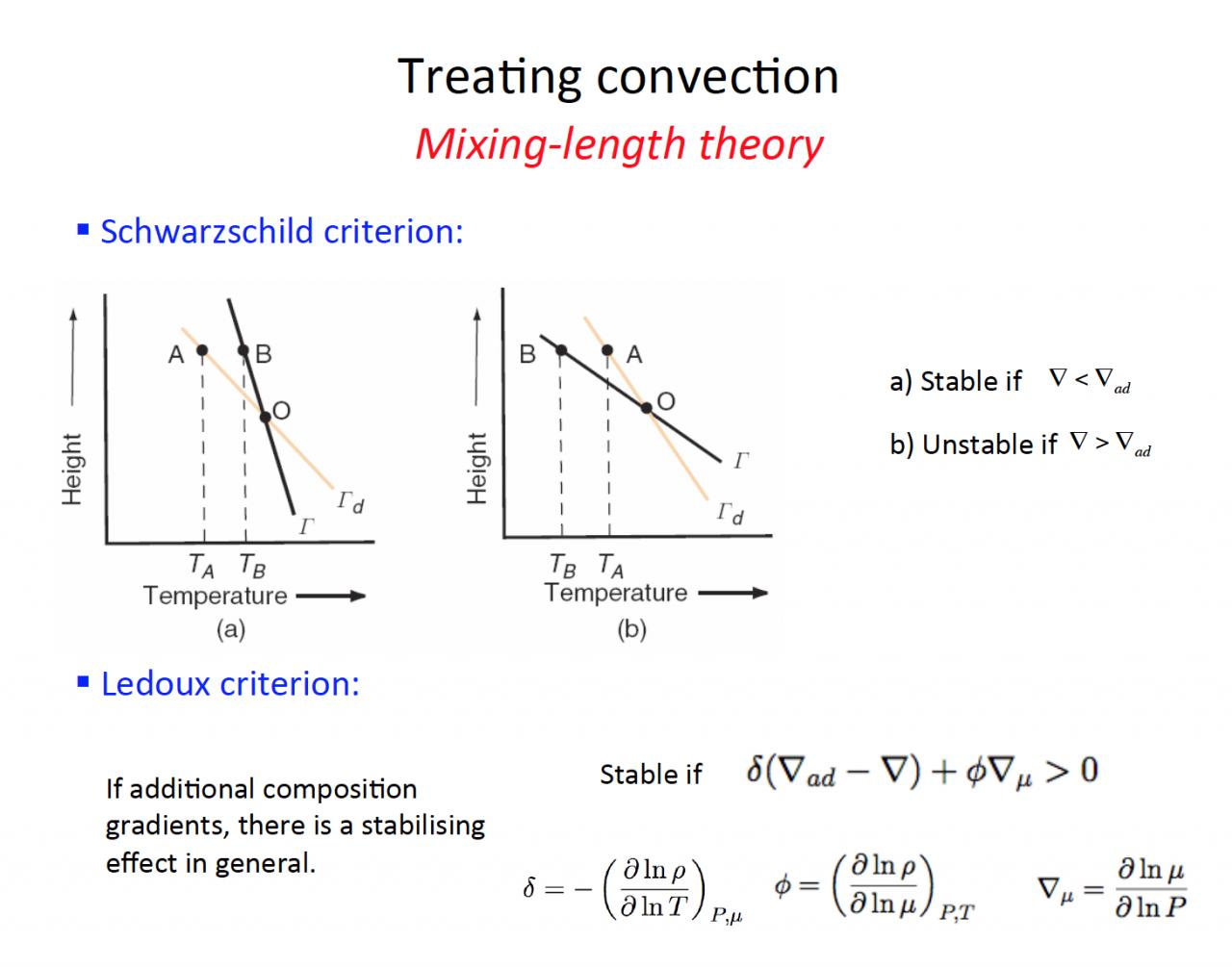
3) Concernant la question avec les 2 schémas : je sais que la convection apparaît quand le gradient de température est supérieur au gradient adiabatique. Il y a donc instabilité pour le schéma a) et stabilité pour schéma b) vis-a-vis de la convection : est-ce correct ?
Le critère de Schwarzschild serait sur le gradient adiabatique ? par exemple, si, Alors il y a convection ?
3)Pour la question 3.b), comment un gradient de poids moléculaire modifie ce critère ?
Je dirais a priori que le poids moléculaire empêche la pénétration de la zone radiative dans la zone convective car la poussée d'archimède serait contre-balancée par la gravité mais je suis pas sûr ?
ou alors son effet serait dans l'autre sens, c'est-à-dire une pénétration de la zone convective dans la zone radiative ?
4) Enfin, est-ce que la convection thermohaline correspond à une pénétration de la convection dans la zone radiative (peut être à cause de ce gradient de poids moléculaire) ou l'inverse (pénétration de la zone radiative dans la zone convective) ?
Dans quel cas alors se produit-t-elle ?
Merci par avance pour votre aide, elle sera précieuse
-----