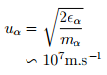Rendement propulsif

[Gilgamesh]

Hello,

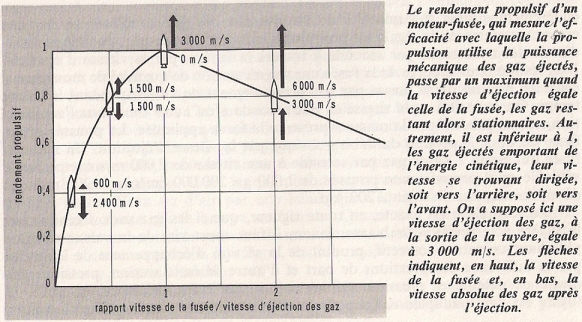
Je cherche à optimiser le rendement propulsif de l'arche (propulsive efficiency) c'est à dire le ratio entre l'énergie qu'elle emporte sur l'énergie dépensée. La plupart des équations sur la propulsion des fusées sont basées sur l'hypothèse d'une vitesse d'éjection u constante (équation de Tsiolkovski). Dans le cadre d'une vitesse d'éjection constante, l'optimum énergétique est atteint quand :

u = 0,6275 Δv (accélération sans freinage)
u = 1,255 Δv (accélération puis freinage)
avec Δv l'incrément de vitesse.

Je sais qu'on peut l'améliorer en éjectant à la même vitesse que la fusée de manière à ce que le gaz éjecté se retrouve au repos par rapport à l'origine du mouvement en sortant de la tuyère, cad en fixant :

u(t)=-v(t) (en notation vectorielle)
à chaque instant t de la trajectoire.

Dans ce cas, le rendement propulsif est de 100% puisque toute l'énergie cinétique se retrouve dans la masse utile en fin de trajectoire. Mais il faut se fixer une vitesse minimum disons u₀, sinon la masse éjectée tend vers l'infini si on part de v=0 au départ. J'aimerais partir d'une vitesse nulle, entamer ma trajectoire avec une vitesse d'éjection u₀ constante, puis une fois que la vitesse du vaisseau a atteint cette vitesse d'éjection, passer à une vitesse d'éjection variable. Puis freiner toujours à u=v jusquà l'atteinte de v=u₀, et là finir le freinage à vitesse d'éjection constante.

J'aimerai exprimer le rendement énergétique global en fonction de cette vitesse minimale u₀. Et pour l'instant je n'arrive à rien, cad que l'énergie dépensée par unité de masse utile reste toujours supérieure au cas u = 1,255 Δv

Où est le loup ? Quelqu'un saurait comment s'y prendre proprement pour résoudre le problème ?
-----

[bintang]

Bonjour,

Je sais qu'on peut l'améliorer en éjectant à la même vitesse que la fusée de manière à ce que le gaz éjecté se retrouve au repos par rapport à l'origine du mouvement en sortant de la tuyère, cad en fixant : u(t)=-v(t) (en notation vectorielle) à chaque instant t de la trajectoire.
Dans ce cas, le rendement propulsif est de 100% puisque toute l'énergie cinétique se retrouve dans la masse utile en fin de trajectoire.

Je voulais juste illustrer le propos avec un exemple de courbe de rendement propulsif issu de 'Fusée et astronautique' de Camille Rougeron et Jean Bodet - Larousse 1964

[Gilgamesh]

Bon, je pense avoir trouver quelque chose, mais comme ça fait 15 pages (écrit gros et aéré, avec les formule) j'ai édité un document LaTeX.

Je ne suis pas contre une relecture critique

Essai d'optimisation de la propulsion d'un trajet interstellaire habité

[PhilAurele]

Bonjour Gilgamesh,

Je ne vais pas t'aider sur la vérification des calculs, j'en serais bien incapable. Il y a par contre 2-3 choses dans le cadre de ta réflexion qui m'interpellent :

1.2 Vitesses : Tu indiques que

Les produits de réactions sont des noyaux d’42He de masse mα

Mais tu ne précises jamais la masse m_α. Dès lors, comment obtiens tu le résultat de l'équation suivante ?


1.4 Masse utile : La masse utile est, si je ne dis pas de bêtise, la masse transportée, indépendante de la masse qui permet d'effectuer le transport. Tu n'indiques pas non plus comment tu parviens au résultat que tu indiques, à savoir :

de l’ordre d’une dizaine de gigatonnes, m ~ 1013kg

Ne devrais-tu pas indiquer les paramètres de base, à savoir a minima le nombre de personnes transportées et les conditions dans lesquelles elles sont transportées. D'autant que sur un voyage aussi long, pour que quelqu'un puisse voir la fin du voyage, encore faut-il qu'il y ait eu reproduction. J'imagine bien que ce n'est pas ton propos mais tu devrais préciser qu'il s'agit d'une hypothèse de travail.

1.5 Energie caractéristique : Tu indiques :

[...]le mobile de masse m[...]

Tu viens d'indiquer que la masse utile a pour symbole m au chapitre précédent et tu attribues ici le même symbole à une masse différente, mais non précisée. Du coup, je ne vois pas comment tu parviens au résultat suivant :

E/m ~ v2 ~ 1013J.kg−1

Mais bon, là c'est sûrement moi qui manque de maîtrise.

[A voir en vidéo sur Futura]

[Gilgamesh]

Bonjour Gilgamesh,

Je ne vais pas t'aider sur la vérification des calculs, j'en serais bien incapable. Il y a par contre 2-3 choses dans le cadre de ta réflexion qui m'interpellent :

1.2 Vitesses : Tu indiques que

Les produits de réactions sont des noyaux d’42He de masse mα

Mais tu ne précises jamais la masse m_α. Dès lors, comment obtiens tu le résultat de l'équation suivante ?
Pièce jointe 274910

Effectivement, ça ne coûte pas grand chose de le préciser.

1.4 Masse utile : La masse utile est, si je ne dis pas de bêtise, la masse transportée, indépendante de la masse qui permet d'effectuer le transport. Tu n'indiques pas non plus comment tu parviens au résultat que tu indiques, à savoir :

de l’ordre d’une dizaine de gigatonnes, m ~ 1013kg

Ne devrais-tu pas indiquer les paramètres de base, à savoir a minima le nombre de personnes transportées et les conditions dans lesquelles elles sont transportées. D'autant que sur un voyage aussi long, pour que quelqu'un puisse voir la fin du voyage, encore faut-il qu'il y ait eu reproduction. J'imagine bien que ce n'est pas ton propos mais tu devrais préciser qu'il s'agit d'une hypothèse de travail.

Pour le coup, il y aurait tellement à dire, que ça déborderait complètement le cadre de l'article. Je laisse ça pour un second qui exposerait la structure de l'Arche.

1.5 Energie caractéristique : Tu indiques :

[...]le mobile de masse m[...]

Tu viens d'indiquer que la masse utile a pour symbole m au chapitre précédent et tu attribues ici le même symbole à une masse différente, mais non précisée. Du coup, je ne vois pas comment tu parviens au résultat suivant :

E/m ~ v2 ~ 1013J.kg−1

Mais bon, là c'est sûrement moi qui manque de maîtrise.

Rigoureusement parlant tu as raison, mais je ne considère dans un premier temps que la seule énergie communiquée à la masse utile, pour montrer qu'elle est considérable en soi. Le calcul de l'énergie se précisera dans la suite de l'article.

J'ai reformulé pour éviter de heurter le lecteur.

Merci pour tes remarques

[Mct92mct]

Bonjour Gilgamesh
J'ai commencé à lire ton rapport sur l'arche...
J'ai bien compris que tu visais essentiellement à faire un parcours d'un dizaine d'années lumière en distance... ce qui m'a interpelé c'est que tu ne te préoccupes pas de la vitesse relative de l'étoile de destination avec la notre...
Sans compter que tu ne parles pas non plus du puits gravitationnel dont il faudra sortir pour quitter notre soleil...
Il me semble que ton calcul est juste un calcul ou on part de la vitesse zéro pour parcourir 10 années lumière et arriver à la vitesse zéro...
Cette approximation est elle bien juste?
Cordialement

[Mct92mct]

Sans compter que tu ne parles pas non plus du puits gravitationnel dont il faudra sortir pour quitter notre soleil...
et dont il faudra se freiner aussi à l'arrivée...
Cette approximation est elle bien juste?
Cordialement

ps: j'ai rajouté le freinage à ma question...

[Mct92mct]

PS: je sais que là, je vais être un peu destructif vis à vis de ton projet... Mais ne vaut il pas mieux attendre que la technologie puisse permettre de relier ces étoiles à 10 années lumière dans un temps propre de 6 ans 2 mois et 21 jours. ça serais plus confortable non?
Surtout qu' à une vache prés... on peut avec la même technologie visiter des étoiles à 5000 années lumières...

[kcnarf07]

Salut,
Le projet se base justement sur l'idée raisonnable qu'une telle technologie ne sera pas à notre portée, au moins à moyen terme. Et que même si elle l'était, les énergies mises en jeu seraient encore plus gigantesques, rendant un voyage relativiste encore plus improbable : "Dans le cadre d’un trajet
interstellaire le seul mode de propulsion situ´e dans notre horizon technologique est la fusion
thermonucl´eaire aneutronique"

Sinon, j'avais moi aussi 2 questions :
- Pourquoi finalement opter pour une utilisation principale du B et Li de l'océan terrestre plutôt que pour des solutions alternatives (lunes joviennes par exemple), sachant qu'à plus long terme, les arches sont sensées se "reproduire" autour d'autres étoiles et donc pouvoir extraire B et Li ailleurs que dans des océans liquides de surface.
- Pourquoi rester fixé sur une durée de voyage de 1000 ans ? allonger à 1200 ou 1400 ans par exemple permet-il une économie de B/Li substantielle ou négligeable ?

Par ailleurs, j'ai parcouru le fil "société du futur" datant de 2005 sur lequel semble être né le projet, et j'ai trouvé assez fascinantes les discussions entre Gilgamesh et Lambda0,
Sur ce sujet comme sur d'autres, c'est toujours un plaisir de lire Gilgamesh, avec sa capacité à mener des raisonnements rigoureux sans pour autant perdre le lecteur néophyte que je suis en route.

[Gilgamesh]

Bonjour Gilgamesh
J'ai commencé à lire ton rapport sur l'arche...
J'ai bien compris que tu visais essentiellement à faire un parcours d'un dizaine d'années lumière en distance... ce qui m'a interpelé c'est que tu ne te préoccupes pas de la vitesse relative de l'étoile de destination avec la notre...
Sans compter que tu ne parles pas non plus du puits gravitationnel dont il faudra sortir pour quitter notre soleil...
Il me semble que ton calcul est juste un calcul ou on part de la vitesse zéro pour parcourir 10 années lumière et arriver à la vitesse zéro...
Cette approximation est elle bien juste?
Cordialement

Effectivement, c'est une approximation mais justifié par le fait que la vitesse relative entre le Soleil et par exemple Epsilon Eridani est de l'ordre de 15 km/s (en vitesse radiale), ce qui représente 0,5% de la vitesse de pointe l'arche dans l'hypothèse d'un trajet à 3000 km/s.

Concernant la vitesse de libération du Système solaire, en partant de Jupiter (à l'aphélie, R = 5,46 UA) le Δv est de 18 km/s. Là encore c'est de deux ordre de grandeur en dessous du Δv global du trajet.

PS: je sais que là, je vais être un peu destructif vis à vis de ton projet... Mais ne vaut il pas mieux attendre que la technologie puisse permettre de relier ces étoiles à 10 années lumière dans un temps propre de 6 ans 2 mois et 21 jours. ça serais plus confortable non?
Surtout qu' à une vache prés... on peut avec la même technologie visiter des étoiles à 5000 années lumières...

L'idée est effectivement qu'un telle techo n'existe que dans nos rêves. Ou comme rappelé par kcnarf que ça nécessiterait des énergies plusieurs ordre de grandeur plus grand.

Ces rêveries, sur la possibilité de rejoindre les étoiles en des durées, disons très inférieures à celle d'une vie humaine, jouent à mon sens un rôle assez néfaste car elle nous incitent à garder l'arme au pied, sans examiner sérieusement les solutions physiquement crédibles.

Sinon, j'avais moi aussi 2 questions :
- Pourquoi finalement opter pour une utilisation principale du B et Li de l'océan terrestre plutôt que pour des solutions alternatives (lunes joviennes par exemple), sachant qu'à plus long terme, les arches sont sensées se "reproduire" autour d'autres étoiles et donc pouvoir extraire B et Li ailleurs que dans des océans liquides de surface.

Je dirais que quelque soit le lieu, la solution qui s'imposera sera la plus facile. Nous disposons des océans terrestres comme source relativement accessible de noyaux fusibles. Mais tu as raison, dans le cadre d'une diffusion galactique, les sources accessibles de noyaux fusibles devraient faire partie des critères de choix d'un système cible.

- Pourquoi rester fixé sur une durée de voyage de 1000 ans ? allonger à 1200 ou 1400 ans par exemple permet-il une économie de B/Li substantielle ou négligeable ?

C'est sans doute vers ça qu'on s'achemine... La difficulté de la réflexion à ce sujet est de savoir jusqu'à quel point optimiser le temps ou l'énergie ? Quel coefficient appliquer pour un choix rationnel ?

Par ailleurs, j'ai parcouru le fil "société du futur" datant de 2005 sur lequel semble être né le projet, et j'ai trouvé assez fascinantes les discussions entre Gilgamesh et Lambda0,
Sur ce sujet comme sur d'autres, c'est toujours un plaisir de lire Gilgamesh, avec sa capacité à mener des raisonnements rigoureux sans pour autant perdre le lecteur néophyte que je suis en route.

Merci

[Mct92mct]

Bonjour,
Effectivement, l'écart de vitesse de 15km/s même associé à la vitesse de libération de départ 18km/s et à une vitesse de freinage à l'arrivée identique, ne compte au total que pour 50km/s au maximum... ce qui fait 1/60 de la vitesse de croisière moyenne de 3000km/s
Tu as donc tout à fait raison de négliger dans un premier temps le puits de potentiel des deux étoiles ainsi que l'écart de leurs vitesses.
Ce qui m'interpelle quand même c'est qu'un tel voyage avec l'arche ne pourra être entrepris qu'avec la certitude qu'il existe au moins une planète dont les conditions de vie "intra muros", eau, conditions atmosphériques, force de gravitation, seront voisines de la notre...
Sans doute sera-t-il plus judicieux d'envoyer en premier, des robots qui n'auront pas besoin de moteurs fusées d'une masse et d'une puissance aussi grande que celle de l'arche... et peut être pourrons nous ainsi avoir nos réponses sur la certitude qu'il existe des planètes satisfaisant le critère de vie "in situ" dans quelques siècles seulement et peut être moins, si la sonde ne fait que passer et n'a donc pas a fournir d'énergie pour son freinage.
Sans compter qu'il serait aussi plus facile de multiplier les tentatives d'essais...
Cordialement

[Gilgamesh]

Ce qui m'interpelle quand même c'est qu'un tel voyage avec l'arche ne pourra être entrepris qu'avec la certitude qu'il existe au moins une planète dont les conditions de vie "intra muros", eau, conditions atmosphériques, force de gravitation, seront voisines de la notre...
Sans doute sera-t-il plus judicieux d'envoyer en premier, des robots qui n'auront pas besoin de moteurs fusées d'une masse et d'une puissance aussi grande que celle de l'arche... et peut être pourrons nous ainsi avoir nos réponses sur la certitude qu'il existe des planètes satisfaisant le critère de vie "in situ" dans quelques siècles seulement et peut être moins, si la sonde ne fait que passer et n'a donc pas a fournir d'énergie pour son freinage.
Sans compter qu'il serait aussi plus facile de multiplier les tentatives d'essais...

1) Il est à mon sens certain que le système distant sera déjà exploré. On ne s'embarque pas à plusieurs dizaines de milliers pour un trajet d'un millénaire sans connaitre de façon assez détaillé le système de destination. Les capacités d'imageries vont connaitre sans doute une progrès considérable dans les prochaines années. Je pense notamment au principe de l'hypertelescope à densificateur de pupille de Labeyrie par exemple. Dans le projet Exo Earth Imager basé sur ce principe, 150 miroirs de 3m disposés sur un diamètre de 150 km permettrait une image directe de la Terre à 10 années-lumière permettant de distinguer la forme des continents.

On peut également utiliser le principe d'antenne gravitationnelle en mettant un observatoire dans l'axe de la cible au point focal gravitationnel du Soleil, à ~550 UA ce qui permet d'utiliser le Soleil lui même comme lentille (gain attendu de 112 dB dans le visible !).

Il sera peut être aussi possible d'accélérer des nano-sondes à des vitesses de l'ordre de c/10 et n pourrait utiliser à nouveau le principe d'antenne gravitationnelle en tandem avec l'étoile cible pour le retour radio. Tous les systèmes d'intérêt situés à moins de 10 al serait explorés de la sorte pendant la construction de l'Arche.

2) Il n'est pas moins certain que dans les système explorée dans le voisinage immédiat du Soleil, il n'existe pas de planète au standard terrestre. D'où l'Arche.

Je me cite : un autre aspect que l’énergie doit également être pris en compte, qui relève non pas du pur domaine de l’astronautique (fusée, moteur…) mais du champs de l’astrophysique et de l’exobiologie. Il concerne la planète-cible ou plutôt le système stellaire cible, tout entier, incluant les petits corps gris (astéroïdes, comètes).

On ne peut accélérer que de petites structures à des vitesses relativistes, vu les ratios M0/M que réclame l’atteinte de telles vitesses. Petites structures qui devraient néanmoins abriter le minimum d’humains permettant d’assurer une diversité génétique suffisante, soit au moins 1000 personnes.

Il est possible de diminuer les exigences de structure dans le cas relativiste en faisant hiberner une fraction appréciable des partants.

Mais c’est avec l’exigence forte que la planète soit immédiatement habitable “tête nue”, c’est à dire sans terraformation.

Sur au moins quelques centaines de km² contigus, il faudrait s’assurer de disposer des conditions d’existence minimales suivantes :
- Gravité : 0,5 - 1,3 g
- Dose annuelle de rayonnement : < 100 milliSievert
- Pression atmosphérique : 0,5 et 5 atm
- Pression partielle d'O2 : 0,1 - 0,5 atm
- Température : -50 et +50°C
- Présence d’eau en surface ou sub-surface
- Absence de gaz toxiques

Pour atteindre les “standards” de la Terre, il faudrait ajouter :
- systèmes climatiques diversifiés basés sur le cycle de l’eau
- océans d’eau liquide
- spectre stellaire à ~6000K
- écosystème accueillant
Or par ailleurs, envisager un stratégie courte pour rejoindre un corps très éloigné implique d’atteindre une cible qu’on ne connait qu’à distance. Car s’il s’agit d’envoyer des sondes automatiques pour explorer préalablement le système, il faut qu’elles-même se déplacent à des vitesses relativistes tandis que les futurs voyageurs se trouvent au repos, attendant que l’information leur revienne par émission radio. Dès lors que la cible se situe au-delà de quelques siècles-lumière, le temps d’attente (un millénaire pour une cible situé à 500 al) excède ce qu’il est possible d’atteindre sans attendre, en stratégie longue en choisissant un système plus proche, même s’il est moins viable, nous verrons pourquoi.

Concernant la fréquence des planètes habitables “tête nue” dans les systèmes stellaires, les prochaines décenies devraient nous en dire beaucoup, et c’est avec beaucoup d’impatience que nous l’attendons. Mais il ne me semble pas présomptueux de prédire que cette fréquence sera faible si l’on considère les exigences énumérées ci-dessus. Par conséquent qu’il y ait fort peu de chances d’en trouver une à proximité, disons à moins de 20 années-lumière.(...)

Et quoique l’astrophysique observationnelle fasse des progrès exponentiels, à quelle échéance peut-on s’attendre à ce que l’observation purement radioélectrique d’un système lointain, situé à des centaines, des milliers ou des dizaines de milliers d’années-lumière nous livre une information si totalement satisfaisante qu’elle autorise à prédire la possibilité de le coloniser “dès l’aterrissage” ? Notamment en ce qui concerne la nature de l’écosystème. Il y a sans doute peu à craindre du très gros (bêtes féroces…) ou du nano (virus, nécessitant un compatibilité des systèmes génétiques). Mais les mico-organismes de types bactériens ou fongiques ne nécessitent pour se développer que d’un substrat organique. En soi le risque reste raisonnable, mais il donne à voir sur le risque global encouru. Tout peut arriver, et tout sera envisagé par les partants de façon bien plus accrue que ne le peut cette réflexion. Une colonie réduite au minimum dans un vaisseau lui-même minimal est livrée pieds et poings liés au moindre imprévu, sans espoir d’aucun secours terrestre, même moral. Or peut-on imaginer plus fertile en imprévus que ce premier trajet hors du système solaire ? Que se passerait-il si les 20 ans prévus se traduisaient par 200 ans de vie confinée ?

De ces éléments, on peut conclure que l’humanité ne peut s’aventurer raisonnablement dans les espaces immenses qui l’entourent qu’en étant rigoureusement autonome et détachée de tout calendrier, sauf en ce qui concerne l’énergie.