Ascenseur spatial

**amenis** · 02/03/2019, 14h03

Bonjour,

Suite a un article de S&V je me suis lancer dans le calcul de la force qui s'exercerait sur le point situé sur l'orbite géo-stationnaire d'un fil qui irait jusqu'au sol.
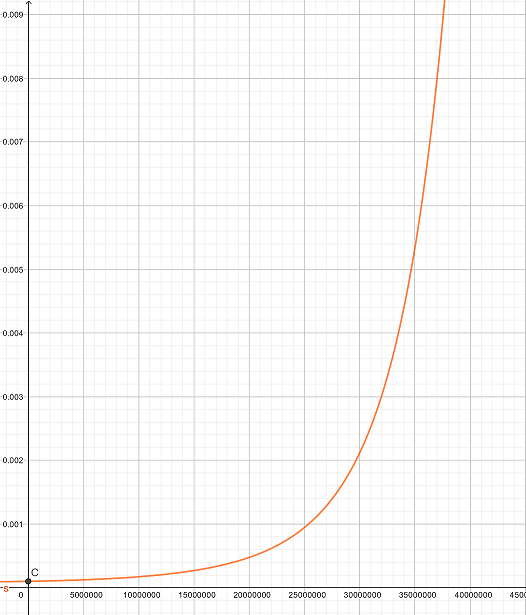
D'abord j'ai calculer la force qui s'exercerait sur une masse m
m.(g0.((R)/(R+h))^(2)-ω^(2).(R+h))
R : rayon terrestre a l'équateur (m)
h : altitude (m)
g0 : accélération de la pesanteur au sol
ω : vitesse angulaire de la terre r.s-1
m : une masse quelconque en Kg (1)

géogébra me trouve bien une racine vers 36000 km (35879309 m exactement)

maintenant je passe a l'intégrale , la fibre de carbone a une densité de 18Kg / m^3 , si je considère un fil de 1 mm^2 de section.

Formule géogébra
a=Intégrale(18.10^(-6)*x* (9.81((6378000)/(6378000+x))^(2)-(2*(3.1416)/(24*3600))^(2) (6378000+x)),0,35879309)

si c'est bien ca la formule , le résultat est
a = 8891149.957883

C'est bien des kilos ? ou je me plante quelque part ?

si j'enlève le premier x (erreur probable)
a=Intégrale(18.10^(-6)* (9.81((6378000)/(6378000+x))^(2)-(2*(3.1416)/(24*3600))^(2) (6378000+x)),0,35879309)

ca me donne 1.38 , difficilement recevable aussi :/

**Dynamix** · 02/03/2019, 14h52

Salut

Envoyé par amenis

la fibre de carbone a une densité de 18Kg / m^3

18 quintaux , pas 18 kg

Envoyé par amenis

a = 8891149.957883
C'est bien des kilos ? ou je me plante quelque part ?

C' est quoi "a" ?

**amenis** · 02/03/2019, 15h04

Envoyé par Dynamix

Salut

18 quintaux , pas 18 kg

Exact merci 1.8g / cm3 -> 1800 Kg / m^3

C' est quoi "a" ?

Variable quelconque qui stock le résultat

**amenis** · 02/03/2019, 15h17

Donc en corrigeant la densité de la fibre de carbone , j'ai ca :
Formule géogébra
a=Intégrale(18.10^(-4)*x* (9.81((6378000)/(6378000+x))^(2)-(2*(3.1416)/(24*3600))^(2) (6378000+x)),0,35879309)

si c'est bien ca la formule , le résultat est
a = 2 912 829 637.702 Kg

Y'a un truc qui va pas ...

A voir en vidéo sur Futura · Aujourd'hui

**amenis** · 02/03/2019, 15h35

c'est sur que ca va pas , avec 1 m3 on fait 1000 km de fil de section 1mm^2.
Donc on ne devrait pas dépasser 1800 * 36 = 64800 Kg

A mOn avis c'est géogébra qui foire complet , et j'ai pas de calculatrice scientifique

**amenis** · 02/03/2019, 15h41

Je pense comprendre mon erreur , il faut que je dérive sur x et intégrer après ...

**amenis** · 02/03/2019, 19h55

Bon ben je comprends pas , sur l'appli Android j'ai pas le même resultat
f=Intégrale(18*10^(-4) (9.81((6378000)/(6378000+x))^(2)-0.0000000052885 (6378000+x)),0,35879309)
f = 87318,70 N

La ça me va bien , autrement dit il faudrait que la fibre de carbone puisse soutenir 8900 kg avec un fil de 1 mm ��

**spibulgroz** · 03/03/2019, 12h31

Bonjour,

Attention aux symboles : ils sont définis clairement, et ne doivent pas être écris autrement que la définition.

Pour kilo, le symbole est k minuscule !!!!!

**amenis** · 06/03/2019, 23h25

Bonsoir,

Je reviens vers vous car j'essaye de prendre en compte une section variable du cable.
Je pars des formules suivantes :
$\text{[math]}$
$\text{[math]}$

ce qui donne :

$\text{[math]}$

Et enfin

$\text{[math]}$

J'ai effectué le tracé dans geogébra, mais la courbe ne me plaît pas. Je m'attendais a avoir une s'' négatif , mais ce n'est pas le cas.

Le tracé est en pièce jointe

**amenis** · 06/03/2019, 23h45

$\text{[math]}$ : masse volumique Kg.m^{3}
$\text{[math]}$ : résistance N.m^{2}
$\text{[math]}$ : rayon de la terre à l'équateur
$\text{[math]}$ : accélération de la pesanteur au sol
$\text{[math]}$ : altitude

Le fichier est pas passé dans le premier post.
Voici ce que ca donne avec de la fibre de carbone
$\text{[math]}$ 1800 $\text{[math]}$
$\text{[math]}$ : $\text{[math]}$ $\text{[math]}$

Nom : space-elevator.png
Affichages : 92
Taille : 55,9 Ko

Nom : space-elevator.png
Affichages : 92
Taille : 55,9 Ko

Fustigator · 07/03/2019, 08h41

Envoyé par amenis

j'ai pas de calculatrice scientifique

Ca m'étonnerait : si vous écrivez sur ce forum on peut supposer que vous avez un PC qui en est doté.

**Dynamix** · 07/03/2019, 10h38

Envoyé par amenis

$\text{[math]}$ : masse volumique Kg.m^{3}
$\text{[math]}$ : résistance N.m^{2}

Chercher l' erreur

(En plus du kelvin.gramme)

**amenis** · 07/03/2019, 14h31

On a l'impression d'être sur le forum 18-25 de JOL , n'y a t'il plus que des trolleurs sur ce forum ?

**zanoloann** · 01/04/2019, 11h11

Tu peux éventuellement utiliser la base de FRENET pour déterminer la force sur ton objet. Après je ne connais pas bien l'utilisation de géogebra donc je ne peux pas t'aider sur sa.

Ascenseur spatial