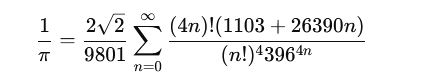Les plus belles formules

[Chiwar]

Bravo CM63, elle est valable pour tout x réel, avec la racine cubique, ça pose pas de problème avec les négatifs : Je l'ai découvert en démontrant des égalités de racines cubiques de Ramanujan
-----

[Deedee81]

Salut,

La vache, ça surprend quand même. Y a moyen de le montrer de manière "simple" ? (voeux pieux mais on ne sait jamais )

[stefjm]

Pour le démontrer ou pour le trouver?
Si tu fais confiance à Mathematica et Alpha, c'est facile à montrer :

https://www.wolframalpha.com/input?i...l%22&key=u9yev

[Médiat]

La vache, ça surprend quand même.

Ben non, c'est le cas pour toutes les formules algébriques exactes, puisque Pi n'est pas algébrique

[Deedee81]

Ben non, c'est le cas pour toutes les formules algébriques exactes, puisque Pi n'est pas algébrique

J'aurais dû y penser. Si c'est bon pour pi alors forcément.....

Mais non ce qui m'a surpris c'est justement que cette formule algébrique soit exacte, pas que ce soit bon pour d'autres valeurs. Et je me demandais si on savait le démontrer facilement.

Pour le démontrer ou pour le trouver?

Démontrer

[Médiat]

En isolant une des racines cubiques, en élevant au cube, et on recommence (je n'ai pas le courage )

[Deedee81]

En isolant une des racines cubiques, en élevant au cube, et on recommence (je n'ai pas le courage )

D'accord, tout bêtement, merci

[stefjm]

Comment cela construit-on ce genre de formule?

[yves95210]

Salut,

Il ne faut pas se laisser impressionner... En posant pour alléger l'écriture, on obtient simplement :



Ensuite, en posant , on obtient :

[Deedee81]

Salut,

Merci Yves, c'est clair (et en effet je m'étais laissé impressionner )

[Chiwar]

bonjour,
c'est en démontrant une égalité de racines imbriquées que je l'ai découverte, elle est facile à démontrer

[Chiwar]

Nouvelle formule d'une racine d'un nombre entier en fonction de racines imbriquées, (elle fonctionne pour tout réel supérieur ou égal à -7)

soit p entier, alors :

[Chiwar]

Excellent, BRAVO POUR LE CHANGEMENT DE VARIABLE..

[Chiwar]

Désolé, j'ai oublié la valeur absolue, le numérateur devient négatif pour p plus grand ou egal que 29



Ainsi pour p=11, cela donne:


pour les valeurs de p inferieurs à 8, on peut les retrouver dans d'autres égalités comme par exemple

[Chiwar]

Quelques applications de la formule génératrice d'égalité de racines imbriquées:

[stefjm]

Salut,
Il ne faut pas se laisser impressionner... En posant pour alléger l'écriture, on obtient simplement :

Ensuite, en posant , on obtient :

En partant de la fin et en remontant, cela donne une méthode pour trouver ce genre de relations.

[yves95210]

En partant de la fin et en remontant, cela donne une méthode pour trouver ce genre de relations.

Tout à fait. Et on doit pouvoir en produire de plus compliquées (en apparence)...

Mais ce n'est pas ce que j'appellerais une "belle formule".

[Deedee81]

Salut,

Mais ce n'est pas ce que j'appellerais une "belle formule".

Et bien cela dépend sans doute de sa définition personnelle de "beau" Mais c'est amusant, car je me faisais la réflexion aussi ce matin : il ne faut pas confondre formules alambiquées et belle formule.

Et autre truc à noter, je viens de faire une recherche sur le net. Et il y a pas mal de sites/forums où on recense les "plus belles formules". Et grosso modo on retrouve les mêmes qu'ici. Mais pas des formules tortueuses.
J'ai l'impression que ce fil est en bout de course.

[pachacamac]

La forme condensée du lagrangien de QCD a aussi belle figure.

[pachacamac]

Explication des symboles de cette formule

[Deedee81]

Je connaissais mais c'est joli en effet

"qui a dit que la QCD était simple". Ca me rappelle l'histoire (apocryphe) que j'avais déjà raconté. Bon elle concerne la MQ mais c'est amusant quand même. Il y a déjà quelques années de ça.
Des physiciens cherchaient à maîtriser de l'électronique à l'échelle mésoscopique (taille des plus petites structures de quelques atomes, avec des puits quantiques).
Soucis : calculs épouvantables.
Un informaticien s'y attaque et revient plus tard avec la réponse, tout fier.
Réponse d'un physicien "ok, l'ordinateur a compris, maintenant on aimerait bien comprendre aussi"
(c'était dans un article qui parlait de l'importance et de la difficulté de visualisation des résultats de calculs informatiques)

[stefjm]

Je n'ai pas vu passé
, n dans Z
avec résultat dans R

[CM63]

Je n'aime pas les logs de nombres complexes, j'affecte de m'y prendre autrement ( et ça m'amuse ) .

[stefjm]

https://fr.wikipedia.org/wiki/Surface_de_Riemann

[stefjm]

L'ordre du groupe Monstre : 2⁴⁶ × 3²⁰ × 5⁹ × 7⁶ × 11² × 13³ × 17 × 19 × 23 × 29 × 31 × 41 × 47 × 59 × 71

[CM63]

Bonjour,

La vision d'une vidéo de Michael Penn m'a fait penser à ces deux formules, que je trouve "belles" :

[stefjm]

[pachacamac]

https://en.wikipedia.org/wiki/Wheele...eWitt_equation

[CM63]

Bonjour,

Une que j'ai vue sur la chaîne YT de Maths 505 :



Que son auteur (l'auteur de la chaîne) considère comme "awesome".