Epuisement d'une ressource vitale et durée de vie d'une civilisation

[sunyata]

L'approche est contestable

Le but du petit calcul était de montrer ce que pouvait apporter un certain taux de récupération lors du recyclage à la durée de vie d'un système.

Et pour des pourcentages inférieurs à 99 % on voit que c'est peanuts.
-----

[Kondelec]

Je suis d'accord mais prendre une base temporelle de 1 an n'est pas réaliste. Si tu veux démontrer quelque chose il faut tacher de le faire avec rigueur.

[sunyata]

Je suis d'accord mais prendre une base temporelle de 1 an n'est pas réaliste. Si tu veux démontrer quelque chose il faut tacher de le faire avec rigueur.

Chaque année un certain nombre de voitures est mis au rebus, je ne vois pas quel problème pose la base temporelle de 1 an, surtout que mon but est uniquement
d'obtenir des ordres de grandeurs.

On a des données assez précises à ce sujet pour les parc existants.

Par exemple :

- Le pourcentage annuel de renouvellement du Parc automobile Français est de 5% par an.
- Aux Etats Unis il est de l'ordre de 7 à 8 % par an.
- En Allemagne il est de l'ordre de 6 % par an.
- Et au niveau Mondial il serait compris entre 7 et 10 % par an.

Donc on peut refaire le calcul avec un taux de renouvellement de 8 % du parc par an.

Ce qui en cas d'épuisement de la matière première donne un durée de demi-vie du système de 28 ans. (au bout desquels le parc à diminué de moitié toutes choses égales par ailleurs)
Avec un taux de récupération du lithium dans le processus de recyclage de 70 %
et taux de recyclage des véhicules de 97,6 %, et ce taux peut potentiellement prolonger la vie du système de 28 ans.

[sunyata]

Si les gisements d'une ressource stratégique sont épuisés, et si on envisage le principe d'une "économie circulaire" pour recycler le stock en exploitation.
Il faut limiter le taux d'érosion annuel du stock à 0,69 % pour prolonger la vie du processus de 100 ans . C'est à dire que le stock de l'année suivante ne doit pas être inférieur
à 99,31 % de ce qu'il était l'année précédente. Avec ce taux le stock à diminuer de 50 % en 100 ans.

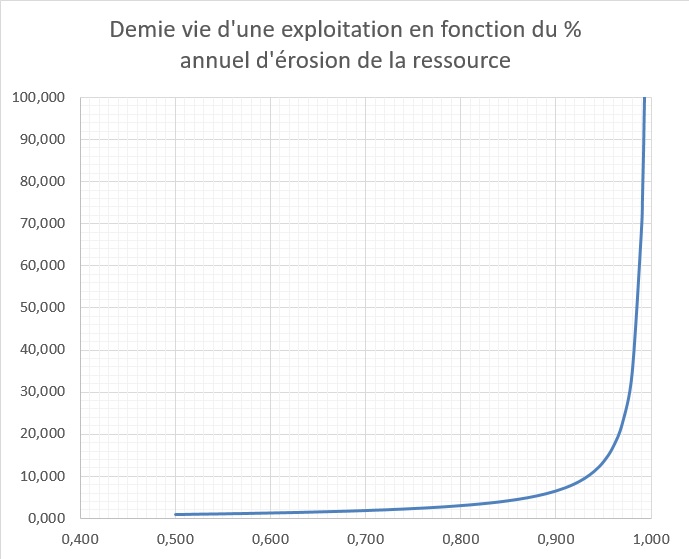
Cela conduit à relativiser quelque peu le concept d'économie circulaire, on ici on envisage même pas le contexte d'une économie en croissance...

[Kondelec]

Pour faire une simulation il faut commencer par poser des hypothèses pour lesquelles tout le monde est d'accord, parce que depuis le début de ce fil tu pars dans tous les sens avec des hypothèses plus ou moins fantaisistes.
Il faut connaitre :
- La quantité de lithium actuellement en circulation
- La quantité consommée par an, avec un taux de croissance estimé (par exemple o estime qu'on consommera +20% tous les ans).
- La durée de vie du batterie lithium
- Le pourcentage de lithium récupéré par retraitement
- Le stock mondial économiquement exploitable.

[sunyata]

Pour faire une simulation il faut commencer par poser des hypothèses pour lesquelles tout le monde est d'accord, parce que depuis le début de ce fil tu pars dans tous les sens avec des hypothèses plus ou moins fantaisistes.
Il faut connaitre :
- La quantité de lithium actuellement en circulation
- La quantité consommée par an, avec un taux de croissance estimé (par exemple o estime qu'on consommera +20% tous les ans).
- La durée de vie du batterie lithium
- Le pourcentage de lithium récupéré par retraitement
- Le stock mondial économiquement exploitable.

Une fois que les gisements d'une ressource sont épuisés, la durée de vie du stock recyclé ne dépend que du taux recyclage.
Si je définis le taux de recyclage de la façon suivante Tr = (Stock circulant l'année N+1/ Stock circulant l'année N)x100

A ce stage il ne peut plus y avoir que de la décroissance à un taux qui dépend directement de Tr.

Concernant l'effet du recyclage dans une économie en croissance l'extrait d'un mémoire intitulé : "Mise au point d’une méthode intégrée d’analyse des impacts des filières de matières premières minérales" me paraît intéressant :

Le recyclage et la croissance (Page 77 )Les métaux demeurent dans le stock de matériaux en utilisation pendant plusieurs années, voire dizaines d’années, et la croissance de la consommation des métaux est forte (voir paragraphe 2.3). De ce fait, même s’il était possible de recycler à 100% (ce qui n’est pas le cas comme vu au paragraphe précédent) les métaux en fin de vie, cela ne permettrait pas un approvisionnement de la demande mondiale.

En effet, l’exemple de l’acier de loin le matériau le plus recyclé au monde, éclaire les limites du recyclage face à la croissance : « au rythme actuel du développement de sa production-consommation de 3,5% par an au cours du XXème siècle, le taux de recyclage actuel au niveau mondial de l’ordre de 62% ne fait gagner à l'humanité qu’environ 12 années contre la raréfaction de la ressource en fer.

C’est-à-dire que la consommation de minerai cumulée au cours du temps sera, en 2012, celle qu’on aurait connue en 2000 sans aucun recyclage. […] Amener, à l’échelle mondiale, le taux de recyclage à un niveau de 90% ne ferait gagner à l’humanité que 8 années supplémentaires. Ce n’est qu’au-dessous de 1 % de croissance annuelle de la consommation mondiale d’une matière première que l’effet positif du recyclage sur la ressource devient important.

Il peut apporter alors sensiblement plus de 100 années de répit, à condition que le taux de recyclage soit très élevé (supérieur à 60-80%)» (Grosse, 2010).

Même un recyclage de « 100 % des flux en fin de vie d’une matière première dont la consommation croît de plusieurs pourcents par an ne produit qu’un effet dérisoire à l’échelle de quelques décennies.

Il n’est donc point d’économie circulaire qui n’inclue un ralentissement de la croissance matérielle et de l’accumulation » (Grosse F., « Économie circulaire » in Bourg & Papaux, 2015).

Ou dit autrement « la clef pour une utilisation soutenable des métaux est d’en utiliser moins. Beaucoup moins » (Patrick Wollants Appendix 2 in Worrell & Reuter, 2014).

[Kondelec]

Non, parce que tu supposes que l’intégralité du stock qui se trouve actuellement dans les mines, plus ce qui est en service, se retrouvera simultanément en utilisation pour participer au recyclage, et que la demande restera constante. C'est une hypothèse qui n'est pas forcément réaliste.

[sunyata]

Non, parce que tu supposes que l’intégralité du stock qui se trouve actuellement dans les mines, plus ce qui est en service, se retrouvera simultanément en utilisation pour participer au recyclage, et que la demande restera constante. C'est une hypothèse qui n'est pas forcément réaliste.

Si on part sur la base de 22 millions de tonnes de réserve, et d'une demande actuelle de 100 000 tonnes/ans, et que nous tablons sur une croissance annuelle de la demande de i = 14 %. (Elle est aujourd'hui de 20%) , alors on arrive à une durée d'exploitation du Lithium de t = 1/i x ln (C/Co) = 36 ans

Si on part de l'hypothèse que l'essentiel du Lithium est destiné au parc automobile : et que la durée de vie des véhicules est de 12 ans, cela donne un taux de renouvellement du Parc de 8,3%

On considère le taux de récupération du lithium de 70 % dans le processus de recyclage.

Ce qui donne un taux annuel de recyclage égal à 1- (8,3%(1-70%) = 97,51% , ce qui donne une durée de vie du stock de 27 ans avant qu'il ne soit diminué de moitié.

On aboutit à une viabilité de l'exploitation du lithium de 36 + 27 = 63 ans.

Comme je n'ai pas pris en compte le recyclage dans la période de croissance de la demande, on peut arrondir à 75 ans en première approximation.

Bonne soirée.

[Kondelec]

Il y a un soucis dans ton raisonnement, ou même plusieurs.
- Pour commencer avec 22 millions de tonnes et 14% tu trouves 36 ans, et tu devrais plutôt trouver un peu plus de 41ans (0.1*1.14^41 = 21.5)
- De plus ce calcul est faux, il ne faut pas calculer le n ieme terme, mais la somme de tous les termes, pour arriver à 22 millions. Cette fois on arrive à un peu plus de 25 ans.
- Par ailleurs tu supposes croissance constante, ce qui n'a pas de sens. Actuellement il y a environ 1.4 milliard de voitures dans le monde, chaque voiture utilise en moyenne 5 à 10 kg de lithium pur, donc pour remplacer la totalité du parc automobile il faudrait environ 7 à 14 millions de tonnes lithium (la quantité dépend de la capacité de la batterie, la capacité dépend du poids et l'autonomie du véhicule).

Faisons une petite simulation, on va supposer que l'on remplace la totalité du parc mondial en 15 ans (ce qui est extrêmement ambitieux, voire même fantasmagorique).
On recycle 75% du lithium des batteries au bout de 15 ans (on ne prend pas en compte celui qui est déjà en circulation).
Une fois que l'on atteint 1.4 milliard de voiture on remplace celles qui ont 15 ans, en gardant un total de 1.4 milliard.

On obtient ceci (un peu moins de 160 ans):


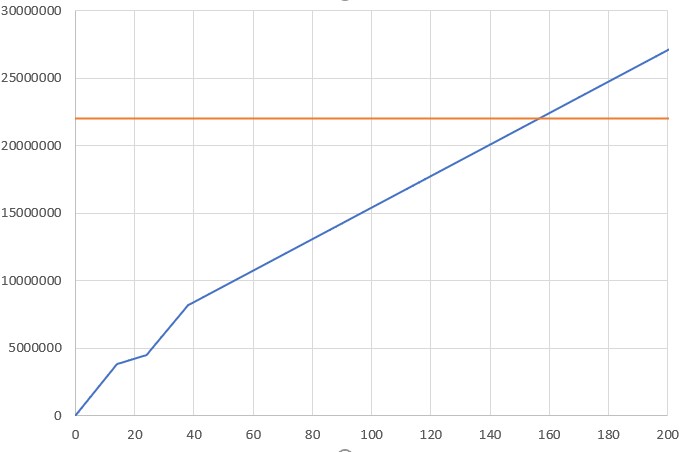
Avec 95% de recyclage le seuil est dépassé en un peu moins de 700 ans.

Rappelons au passage qu'on ne parle ici que du lithium "économiquement exploitable", il y a environ 4 fois plus dans des gisements difficilement exploitables, et environ 10 000 fois plus dans l'eau des océans.

[sunyata]

Bonsoir,

Avec 95% de recyclage le seuil est dépassé en un peu moins de 700 ans.

Peux tu expliquer ce que représentent les 700 ans ? La durée d'exploitation du Lithium ? Cela me parait astronomique...
Au bout de combien d'années d'exploitation le stock de lithium aura-t-il diminuée de moitié selon ton évaluation ?

------------------------------------------------------------------------------------------------

Bon ça vaut ce que ça vaut mais de mon côté j'ai affiné mon calcul. Le cumul du stock à raison d'un taux de croissance i = 14% peut-être calculer selon la formule : C(t) = Co x e^i.t
où Co est le besoin initial de 100 000 tonnes. La formule équivaut à la somme de tous les termes, si on discrétise le calcul.

Remarque :
On peut utiliser cette formule pour calculer C(t) l'évolution d'un Capital Co placé à I%
Par exemple 100 Euros placé à 4% donne avec la formule placé sur 10 ans : 149 euros.

On peut à partir de cette formule isoler t = 1/i x ln(C(t)/Co)
Ainsi en l'absence de recyclage avec un taux de croissance de 14% la formule donne 38 ans pour épuiser le gisement de 22 000 000 tonnes

En se basant sur une durée de vie d'un véhicule électrique de 12 ans on obtient un taux de renouvellement du Parc égal à 1/12 = 8,3 %

Et en prenant un taux de récupération du lithium dans le processus de recyclage égal à 70% sur 8,3% des véhicules du Parc, on apporte 2,49 % du Lithium qui ne doit pas être fourni
par le gisement.

Donc pour calculer la durée de vie du gisement avec le recyclage cela donne : 1/(0,14(1-0,0249)).ln(22 000 000/100 000) = 39 ans.
Une fois le gisement épuisé, on ne peut plus compter que sur le recyclage pour continuer l'exploitation du Parc :
Et le temps pour que le stock atteigne 50% de sa valeur = ln(0,5)/ln(1-2,49/100) = 27 ans.

Cela donne une durée d'exploitation du Lithium de 39 + 27 = 66 ans. le stock de 22 000 000 de tonnes initial a diminué de moitié.

Mais je reconnais qu'une croissance de la demande de 14% par ans n'est peut-être pas une hypothèse réaliste...

Cordialement

[Kondelec]

Mais je reconnais qu'une croissance de la demande de 14% par ans n'est peut-être pas une hypothèse réaliste...

actuellement nous avons 42 millions de voitures électriques dans le monde.
Avec un taux de 14%, au bout de 66 ans, nous avons 651 milliards de voitures.
16 milliards au bout de 38 ans.

Est-ce que tu comprends le problème de ta démarche ?

années	nouvelles voitures	total
0	 -   	14
1	 16 	 30 
2	 18 	 48 
3	 21 	 69 
4	 24 	 93 
5	 27 	 120 
6	 31 	 151 
7	 35 	 186 
8	 40 	 226 
9	 46 	 271 
10	 52 	 323 
11	 59 	 383 
12	 68 	 450 
13	 77 	 527 
14	 88 	 615 
15	 100 	 715 
16	 114 	 830 
17	 130 	 960 
18	 148 	 1 108 
19	 169 	 1 278 
20	 193 	 1 470 
21	 220 	 1 690 
22	 251 	 1 941 
23	 286 	 2 227 
24	 326 	 2 553 
25	 371 	 2 924 
26	 423 	 3 347 
27	 483 	 3 830 
28	 550 	 4 380 
29	 627 	 5 007 
30	 715 	 5 723 
31	 815 	 6 538 
32	 929 	 7 467 
33	 1 059 	 8 527 
34	 1 208 	 9 734 
35	 1 377 	 11 111 
36	 1 570 	 12 681 
37	 1 789 	 14 470 
38	 2 040 	 16 510 
39	 2 325 	 18 835 
40	 2 651 	 21 486 
41	 3 022 	 24 509 
42	 3 445 	 27 954 
43	 3 928 	 31 881 
44	 4 477 	 36 359 
45	 5 104 	 41 463 
46	 5 819 	 47 282 
47	 6 634 	 53 915 
48	 7 562 	 61 478 
49	 8 621 	 70 099 
50	 9 828 	 79 926 
51	 11 204 	 91 130 
52	 12 772 	 103 902 
53	 14 560 	 118 463 
54	 16 599 	 135 061 
55	 18 923 	 153 984 
56	 21 572 	 175 556 
57	 24 592 	 200 148 
58	 28 035 	 228 183 
59	 31 960 	 260 142 
60	 36 434 	 296 576 
61	 41 535 	 338 111 
62	 47 350 	 385 460 
63	 53 978 	 439 439 
64	 61 535 	 500 974 
65	 70 150 	 571 125 
66	 79 972 	 651 096

[sunyata]

actuellement nous avons 42 millions de voitures électriques dans le monde.
Avec un taux de 14%, au bout de 66 ans, nous avons 651 milliards de voitures.
16 milliards au bout de 38 ans.

Est-ce que tu comprends le problème de ta démarche ?

Oui en effet tu as raison, c'est absurde !

Je suis bon pour revoir ma copie,
merci à toi lol

[sunyata]

Par contre je pense que cette partie là de mon calcul est correcte :

Une fois le gisement épuisé, on ne peut plus compter que sur le recyclage pour continuer l'exploitation du Parc :
Et le temps pour que le stock atteigne 50% de sa valeur = ln(0,5)/ln(1-2,49/100) = 27 ans.

Avec un taux de récupération du lithium dans le processus de recyclage de 70 %, et un taux de renouvellement des véhicules de 8,3% par ans.

[sunyata]

Concernant l'impact du recyclage la fonction qui exprime le facteur multiplicatif est : E = 1/(1-r)
où r est le taux de recyclage.

Par exemple si un gisement dure t = 3 ans sans recyclage, alors il durera t x E avec un taux de recyclage de r



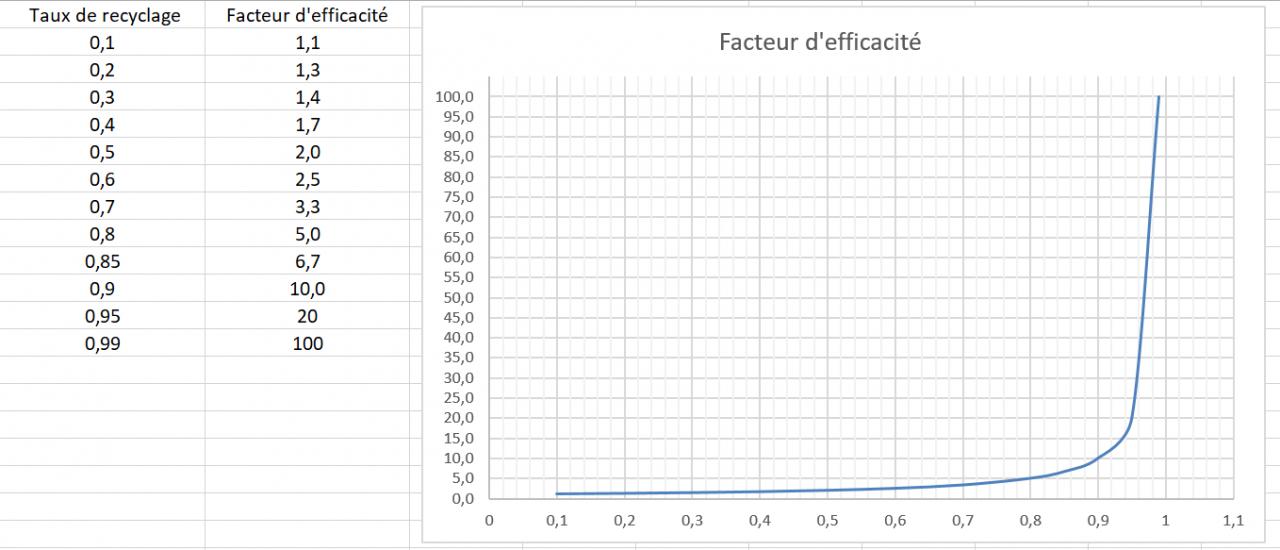
Cela montre toute l'importance du recyclage car avec un taux r de 80% de recyclage on multiplie par E = 5 la durée d'exploitation du gisement.

L'impact du recyclage est conséquent pendant toute la durée d'exploitation d'un gisement, par contre une fois le gisement épuisé, le recyclage permet de gagner quelques années d'exploitation à condition d'avoir des taux de recyclages supérieur à 90%.