qui sait jouer avec les quadripoles !

[recreators]

Bonjour , j'ai un cas particulier de quadripole dont il nous faut calculer la matrice d'impédance , j'ai besoin d'aide ! (voir pièces jointes)

-----

[annjy]

Bon,
soit troll
soit gag
soit pas au niveau......

https://fr.wikipedia.org/wiki/Quadrip%C3%B4le

cdlt,
JY

[recreators]

bah , moi aussi j'ai pensé que c'est juste une question piège , mais il faut prouver la réponse au professeur c'est ça le probléme

[Jack52]

Je pense qu'il serait bon que tu relise ton premier post recreators.

[A voir en vidéo sur Futura]

[invite03481543]

Bonsoir,

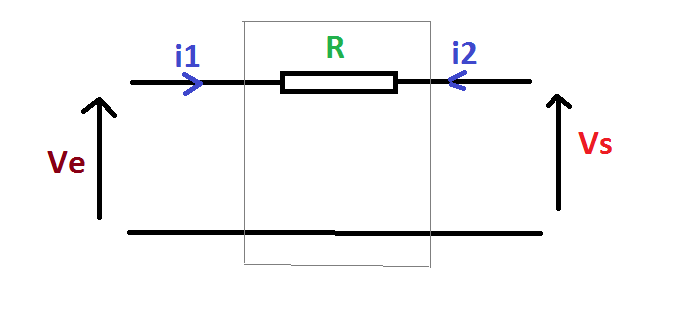
Dans ton circuit il n'y a pas d'impédance.
Néanmoins tu peux écrire les 2 relations simples suivantes:

Vs = Ve + R*I2
I1 = -I2

Puis tu identifies avec la représentation suivante:
Vs=T11*Ve + T12*I1
I2=T21*Ve + T22*I1

Tu en déduis que T11 est sans dimension, T12 est une résistance, T21 une conductance, T22 est sans dimension.

La matrice de transfert est donc:



Tu peux en déduire la matrice que tu cherches en appliquant un raisonnement identique.

[mizambal]

Oui je pense comme vous, la question est un piège !

[invite03481543]

Il n'y a aucun piège....
ve, i1, vs, i2 représentent les ports (entrée et sortie), l'appellation quadripôle est donc respectée.

[mizambal]

Pour info en fouillant dans l'historique j'ai trouvé ça : http://forums.futura-sciences.com/el...uadripole.html
Au 3e message l'auteur dit que ça bloque, il tombe sur des valeurs infinis. Puis Antoanne et d'autres confirment que la matrice impédance n'existe pas pour ce montage ..

[invite03481543]

Je crois avoir suffisamment répondu au post #5.
Je ne vais pas faire tout l'exo, c'est la convention ici.
Je ne comprends pas bien ce qui vous pose problème pour écrire un raisonnement et conclure.
Dans le lien que tu postes, il y en a un qui parle de dipôle alors qu'il y a une entrée sur 2 fils et une sortie sur 2 fils, comme quoi ....
C'est un sujet théorique, c'est donc fait pour réfléchir.
Ce que je vous laisse faire

[invite03481543]

J'ai le sentiment que vous êtes plus prompt à rechercher les solutions sur le net ou sur wiki que d'appliquer un raisonnement simple.
C'est une misère....

[mizambal]

Vous avez le droit de vous tromper également sur ça

[invite03481543]

Dis moi où je me trompe dans ce cas.
Pas quand je lis ton post#8.
Le post #3 exprime ce qui est attendu par le professeur: une démonstration, donc un raisonnement pas une recherche sur google qui est chez certains un bien mauvais réflexe....
Vous avez un cerveau alors servez-vous en.

[mizambal]

L'erreur c'est d’affirmer qu'il n'y a pas de piège. Comme les équations du circuit ici ne permettent pas de déterminer les expressions des coefficients matriciels de l'impédance, à mes yeux il y a bien un piège.

[invite03481543]

Avec un raisonnement bien mené il n'y a pas de piège.
L'infini est un résultat en physique.
C'est différent que d'affirmer qu'on ne peut pas déterminer un résultat.

[invite03481543]

Définition de piège dans le Larousse: Difficulté, problème volontairement dissimulé pour provoquer une erreur en cas d'inattention ou d'ignorance

Tout est dit.

[mizambal]

Concrètement allez trouver un cours/exo de math ou de physique se basant sur une matrice à coefficient(s) infini(s) .. Vous allez chercher longtemps à mon avis ..

[invite03481543]

Si tu le dis.

[Antoane]

Bonsoir,

Bien joué hulk28, tu as eu le mot de la fin.

Si on pouvait à présent rester sur des considérations purement techniques...

[erff]

Bonjour,

La matrice impédance n'est en effet pas définie dans ton exo. Et il y a un moyen très simple de le savoir avant même de poser un seul calcul.
On veut exprimer 2 paramètres de sortie (ici on choisit les tensions) en fonction de 2 paramètres d'entrée (ici on choisit les courants). Si dans le schéma, on s'aperçoit que les paramètres d'entrée sont liés par une relation qui ne fait pas intervenir les paramètres de sortie (dans ton schéma il est clair que Iin=-Iout) alors on ne pourra pas aller plus loin : il faut redéfinir les paramètres d'entrée/sortie. Je suis toujours tombé sur des cas où cette liaison entre paramètres sautait aux yeux en regardant le schéma.

Un autre exemple classique : le modèle du transformateur sans fuite. Il est clair que l'on a toujours Vout=n2/n1*Vin, par conséquent, on ne peut pas définir de matrice admittance.

Des fois il "faut forcer le passage" en ajoutant un élément dans le circuit (genre, une résistance parallèle dans ton schéma) qui rend définie une telle matrice car elle nous arrange.
Si on veut étudier par exemple un transformateur avec ces condensateurs parasites, on a tout intérêt à utiliser des matrices admittance (car les admittances parallèles s'ajoutent donc c'est simple). Dans ce cas, on peut très bien ajouter une résistance série au transfo (ou une inductance de fuite), faire le calcul (somme des matrices admittances), inverser la matrice admittance finale pour avoir la matrice impédance finale et faire tendre le terme ajouté artificiellement vers 0 (si impédance série) ou vers +oo (si impédance parallèle). Ceci marche aussi très bien quand les matrices qu'on veut ajouter n'ont pas les mêmes dimensions.

[invite03481543]

Des fois il "faut forcer le passage" en ajoutant un élément dans le circuit (genre, une résistance parallèle dans ton schéma) qui rend définie une telle matrice car elle nous arrange.

Bonjour,

c'est pas "des fois", c'est "toujours" dans la vraie vie.
Par exemple l'exemple du transformateur n'a aucun sens d'être traité dans le cas idéal, comme d'ailleurs tous les cas idéaux, hormis dans le monde scolaire qui ne met pas suffisamment l'accent sur le danger de cette approche minimaliste.
Le transformateur s'étudie avec la modélisation de Kapp, passage obligatoire et minimum pour étudier un tel composant dans un contexte concret.
L'apprentissage par les cas idéaux explique en grande partie pourquoi les nouvelles générations ont le plus grand mal à appréhender les composants inductifs et les principes analogiques en particulier.
Un exemple précis, souvent abordé ici, est le Flyback.
Dissocier R,L et C dans les méthodes d'apprentissages est une erreur fondamentale qui conduit irrémédiablement à une vision faussée des principes fondamentaux qui régissent le domaine de l'électronique et qui conduit immanquablement à des blocages conceptuels forts.
On observe les mêmes verrous dès qu'on aborde les phénomènes CEM, le routage, etc.
Je ne parle même pas des hyper fréquences où là le blocage est quasi total...