Bonsoir à tous,
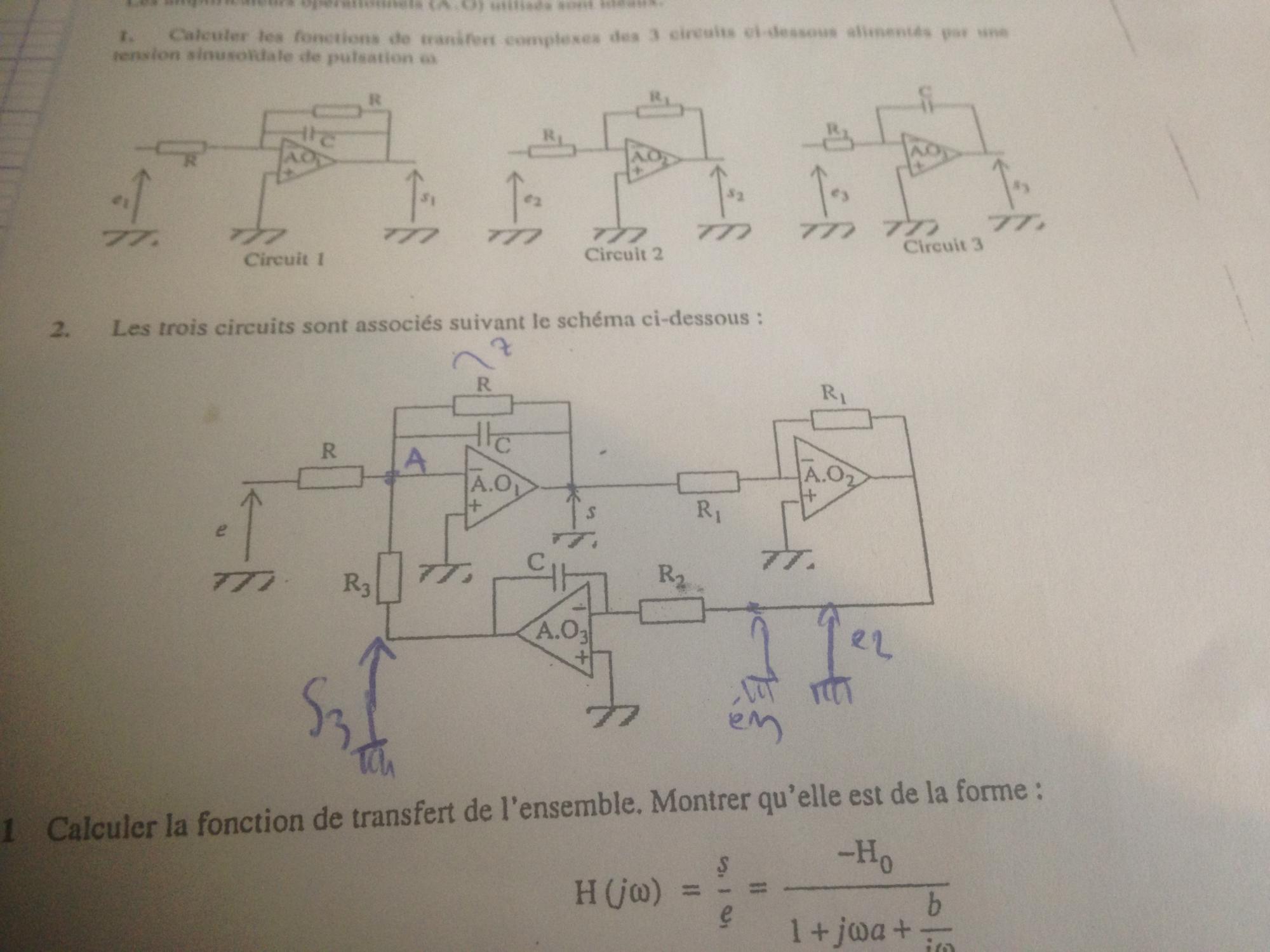
Voila j ai un problème concernant le montage intégrateur d AOP
Je vous donne en pièce jointe les photos :
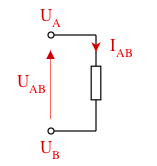
Voila je ne comprends pas pourquoi la prof a écrit Ve=R.I et non pas Ve=-R.I
Je n ai pas compris pourquoi i et Ve sont dans le même sens et pourquoi c est pas le cas avec le condensateur
Apparemment ce serait lie a la loi des mailles ( d ou la présence de flèches)
IMG_4111.jpg
IMG_4112.jpg
-----