L'effet du nombre d'échantillons sur la FFT

[Matlabo]

Bonjour,
Ça fait un certain moment que je bloque sur un truc et je sens que je perds du temps pour un truc pas forcément bien compliqué.

On a un signal composé d'une somme de deux exponentielles complexes de fréquences f1=1680 Hz et f2=1780 Hz échantillonnées à fe= 8 kHz, et de même amplitude.

Puis on nous demande de:
1) Faire le calcul sur 32 échantillons en prenant une FFT sur N= 256 points fréquentiels puis sur N=1024. Les sinusoïdes sont-elles résolues ? Interpréter les
résultats obtenus en calculant f2-f1 et fe/32 ?

==> Il n y a qu'un seul pic alors qu'il devrait y en avoir deux, et j'arrive à comprendre pourquoi ?

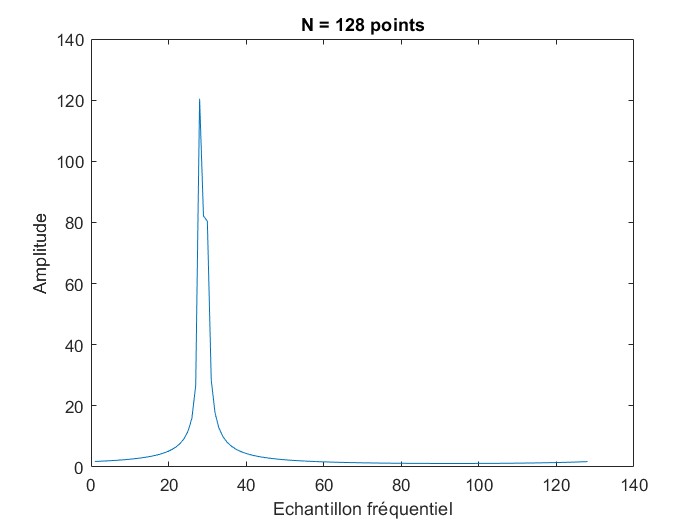
2)Refaire le calcul sur 128 échantillons. Les sinusoïdes sont-elles résolues ? Calculer fe/128 et Interpréter ?

==> Là on a bien 2 pics


Est-ce que quelqu'un pourrait m'expliquer comment le nombre d'échantillons joue sur la justesse du résultat de la FFT ?

Merci !
-----

[Antoane]

Bonjour,

Si le signal temporel ne contient que N=32 échantillons, alors la FFT ne peut contenir plus de 32 échantillons "utiles" (les autres sont une interpolation), et la distance fréquencielle entre deux échantillons est, en vertue de Nyquist-Shannon, de Fe/2N. La distances entre les composantes harmoniques du signal incident étant inférieure à cette valeur, il n'y a pas un point de la fft pour chaque composante spectrale (plus un point à zéro entre les deux pour assurer la présence de deux pics).

[Matlabo]

Je suis pas sûr mais je pense avoir un peu compris


Sur matlab je viens de générer 128 échantillons du même signal qu'en haut, je l'ai soumis à une fft de 128 points, et à ma plus grande surprise je n'ai eu qu'un seul pic ?! Vous pouvez m'expliquer pourquoi ?

[Antoane]

Peux-tu partager ton code complet et le résultat ?

[A voir en vidéo sur Futura]

[Matlabo]

Voila

fe = 8000;
f1 = 1680 ;
f2 = 1780;

n =0:127;
S = exp(1j*2*pi*f1*n/fe) + exp(1j*2*pi*f2*n/fe) ;

TF = fft(S, 128);

plot(abs(TF));
xlabel('Echantillon fréquentiel')
ylabel('Amplitude')
title('N = 128 points')

[Matlabo]

J'ai l'impression qu'il y a des notions de résolution et de précision que je n'ai pas compris

[Antoane]

Bonjour,

Si tu avais un signal purement harmonique échantilloné sur un multiple entier de 2*pi en respectant Nyquist-Shannon, la FFT serait "comme dans les livres" : un unique point, à la fréquence idoine, et tout le reste à zéro.
En revanche, si le signal n'est pas échantillonné sur une période exactement multiple de 2*pi, alors le pic s'élargit, ce n'est plus un dirac. Cela s'explique par le fait que la FFT "périodifit" le signal : la FFT donne le spectre d'un signal de périodique de période la durée de l'enregistrement. Or, si tu n'enregitres pas un nombre entier de périodes, le signal dont tu prends le spectre n'est pas exactement celui qui t'intéresse (en pratique, c'est pour cela qu'on utilise des fenêtres d'apodisation telles que Hamming, Blackman, etc.).
Lorsque tu as un signal avec deux composantes harmoniques, si l'enregistrement n'est pas de durée un multiple entier de la période de chaque signal, il y aura étalement des pics autiour des fréquences de chaque pic. Si les fréquences sont proches, les pics se mélangent et on peine à les distinguer -- même si la résolution fréquentielle de la fft devrait le permettre.

J'espère que c'est clair... ce n'est pas évident à expliquer mais se voit assez bien en jouant avec matlab, en observant les signauy idéaux et leur spectre / FFT et en altérant les signaux peu à peu.

[Murayama]

Bonjour!


Les fréquences de f1 et f2 diffèrent assez peu par rapport à la fréquence limite fe/2.
100 Hz sur 4000, c'est 2.5 %. Donc le problème de départ étant un pas de fréquence
normalisée de 1/32 (soit un peu plus de 3%), vous ne pourrez évidemment rien voir avec
32 échantillons.
Avec 128, on a plus de chances de voir quelque chose. MAIS: les échantillons sont
pour ainsi dire consécutifs, et en plus ils ne tombent pas sur des fréquences "justes"
(au sens de la FFT), mais sur des valeurs quelconques qui correspondent à des valeurs
proches de 27*128 et 28*128. Comme ces valeurs ne seront pas représentées
par un nombre entier de périodes dans le signal temporel, elles vont s'étaler en
fréquence.


NB: il est toujours intéressant de parler en fréquences normalisées. 1 représente la
fréquence d'échantillonnage, toutes les autres fréquences sont entre 0 et 1, et les
fréquences utiles sont entre 0 et 0.5.
Dans votre cas, par exemple si vous aviez un échantillonnage à 16k et les fréquences
f1 et f2 à 3360 et 3560 respectivement, la FFT serait exactement la même au bit près.

Sur matlab je viens de générer 128 échantillons du même signal qu'en haut, je l'ai
soumis à une fft de 128 points, et à ma plus grande surprise je n'ai eu qu'un seul pic ?!
Vous pouvez m'expliquer pourquoi ?

Facile! Vous avez 2 pics proches, mais étalés.
De plus, le pic à 1680 est assez proche d'une valeur en n / 128 puisque c'est
26.88. Par contre le pic suivant, 28.48 est presque au milieu de 2 fréquences en 2kpi/n,
donc plus étalé. Comme la FFT conserve la puissance, (Parceval ou Parseval), s'il est
plus étalé, alors le pic est plus petit. On peut donc prévoir soit un pic assez grand à
1680 et un pic plus petit à 1780, soit un pic à 1680 avec une bosse (pas exactement un
vrai pic) à 1780. On peut même prévoir que comme on a un pic à 28.48 à presque égale
distance entre 28 et 29, il va y avoir 2 fréquences consécutives qui vont se partager
le gâteau avec presque la même valeur, et en pratique c'est exactement ce que vous constatez.


Maintenant, si vous échantillonnez à 1024 échantillons, les choses changent. J'ai changé
juste le premier index et le nombre d'échantillons dans mon tableur. Les 2 nombres au
milieu montre la fréquence normalisée correspondante (l'index) pour les fréquences f1
et f2. Vous voyez que 214.04 est très près de 215, Ce qui veut dire que la fréquence
216 ne va capter que 4% de la fréquence de cet échantillon, ce qui se traduira par
un pic beaucoup plus net. Pour l'autre, on est à 0.12 de 228, donc le pic à 228 sera
relativement net.


On parle beaucoup du fenêtrage qui peut changer un peu les choses, mais il ne faut jamais
en attendre des miracles. J'avais fait un programme FFTMadness qu'il faudrait que je
recompile. Il y avait un potentiomètre linéaire pour la fréquence et des cases à cocher
pour les fenêtres qui permettaient de voir en temps réel l'effet de la FFT...
À propos des fenêtres, on notera aussi que la fenêtre de Hanning n'existe pas, mais
Hamming existe. La fenêtre de Hanning a été créée par un mec qui s'appelait Hann, c'est
donc une fenêtre de Hann. Dans le civil, il était kinésithérapeute (Hann, masseur Hann).
Mais bon, tout le monde fait l'erreur, même mon oscillo Tektronix.


Pascal

[Matlabo]

Merci pour vos réponses !!
Là je suis en cours, je lis tout ça et je vous réponds ce soir !

[FDFD]

Bonjour,

Ayant pas mal utilisé la FFT dans mon boulot, je me permets de faire part de ma compréhension.

Quand on fait une analyse spectrale par TF il faut connaître la fréquence maxi Fmax du signal à analyser pour déterminer la fréquence d’échantillonnage Fe nécessaire pour obtenir un spectre sans repliement.
Fe > 2 x Fmax
Dans votre cas, la condition est tout à fait remplie :
f1 = 1680 Hz
f2 = 1780 Hz
fe = 8000 Hz

Ensuite, il faut se demander quelle résolution spectrale Delta_F on va avoir :
Delta_F = 1 / 2 / Tobs (ou ~1 / Tobs si apodisation)

Tobs est le temps d’observation du signal.

Dans votre cas si on veut résoudre les deux pics, il faut une résolution spectrale meilleure que (1780 – 1680) / 2 = 50 Hz. Cette résolution correspond à un temps d’observation minimal de 1 / 50 = 0.02 secondes.

Enfin, quand on utilise la FFT, il faut se demander quelle va être la résolution de la représentation graphique. Cette résolution peut être améliorée par la technique de « zero filling » qui consiste à prendre un vecteur à transformer bien plus long que le vecteur des échantillons. Le vecteur traité par l’algorithme FFT est alors le vecteur des échantillons complété par des zéros.

Bon amusement !

[Vincent PETIT]

Bonjour,
Le sujet est intéressant, j'utilise aussi l'outil FFT, celui de l'oscillo, mais je n'en ai jamais conçu.

Sans dévier le sujet de Matlabo, est ce une erreur de dire que si le nombre de point de la FFT est fixé à 1024 (souvent le cas sur les oscillos entrées de gamme) alors la fréquence d'échantillonnage doit être un multiple de 1024 (1.024kHz, 10.240kHz, 102.400 kHz) ?

[Matlabo]

C'est quand même super de discuter avec des gens qui savent de quoi ils parlent, ça change ...

Merci !

[Murayama]

Bonjour!

ça change ...

Ça change de quoi? De l'éducation nationale?
Le fait est que je n'ai vraiment compris la FFT que quand je me suis mis à l'utiliser dans la vie
réelle. Avant, je ne faisais qu'utilliser les résultats de cours pour résoudre les problèmes de cours,
comme tous les autres, d'ailleurs. En gros on vous écrit l'intégrale de convolution, et demerdotis
cum bordellem, au lieu d'expliquer vraiment ce qui se passe. Les seuls qui ne bronchent pas sont
les geeks qui intégreront Normale Sup pour ensuite enseigner de la même façon. Dommage.

Pascal

[bobflux]

Sans dévier le sujet de Matlabo, est ce une erreur de dire que si le nombre de point de la FFT est fixé à 1024 (souvent le cas sur les oscillos entrées de gamme) alors la fréquence d'échantillonnage doit être un multiple de 1024 (1.024kHz, 10.240kHz, 102.400 kHz) ?

La FFT est juste un algo qui transforme un tas de nombres en un autre tas de nombres de même taille. La valeur physique de la fréquence d'échantillonnage du signal n'intervient à aucun moment dans le calcul, en fait la FFT n'en a aucune notion. Connaître la fréquence d'échantillonnage te permet simplement, en tant qu'utilisateur de la FFT, de savoir à quelle fréquence physique correspond chaque point dans la sortie de la FFT.

Par contre, si la taille de la FFT est fixée à 1024 par l'appareil, il faut que la fréquence d'échantillonnage permette aux 1024 échantillons de bien couvrir le signal que tu veux étudier, dans l'idéal il faut avoir plusieurs périodes de capturées, une dizaine au moins, sinon il est impossible de distinguer la fenêtre d'apodisation et le signal. Et si la fréquence d'échantillonnage est trpo élevée et que les 1024 points ne contiennent pas une période complète, là ça ne marche plus du tout. Je suppose que ton oscillo doit faire ça automatiquement en fonction de la plage de fréquences sélectionnée pour la FFT. Mais, par exemple, si ton signal fait 100Hz, avec une FFT limitée à 1024 points tu vas devoir utiliser une fréquence d'échantillonnage basse, donc tu verras pas le bruit HF sur ta FFT si il est présent. Et si tu augmentes la plage de fréquences, tu verras le bruit HF mais tu verras plus le signal.