Bonjour, je m’intéresse à pas mal de choses mais j'ai trop peu de logique, il m'arrive néanmoins de penser juste et "loin" mais sans pouvoir expliquer formellement ma position. Je cherche donc à développer ma logique dans une approche adaptée à mes capacités qui sont plus dans l'analogie, le fait descriptif et surtout à pouvoir enrichir ma capacité à nommer les concepts.
Est ce que ce genre d'approche existe , quels auteurs/ouvrages ?
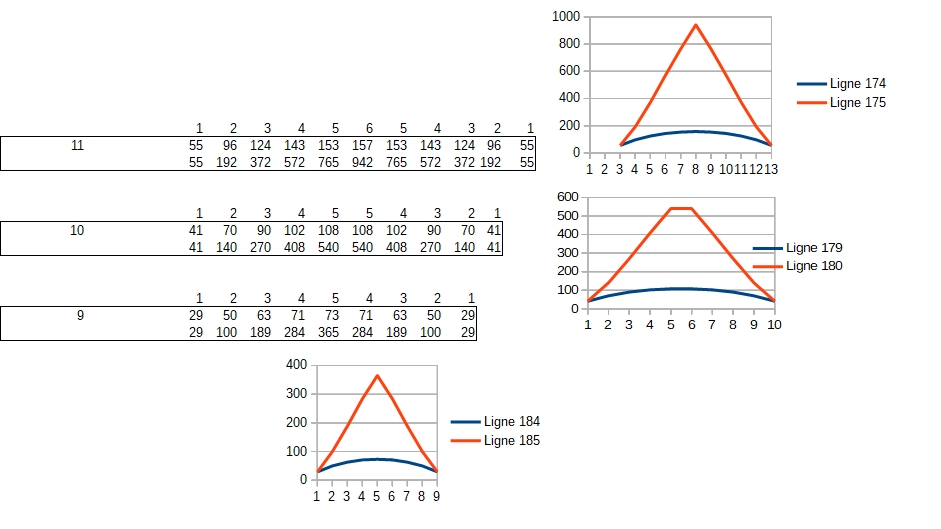
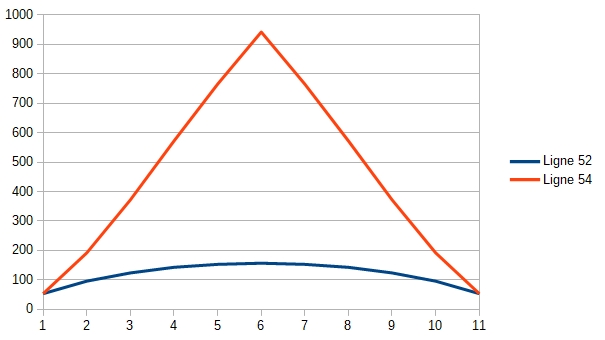
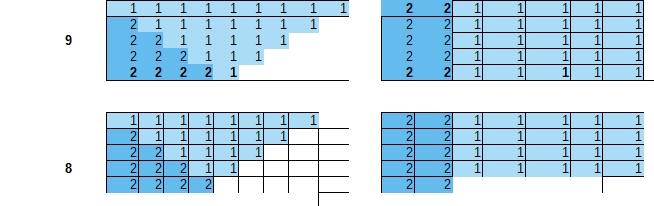
Par exemple depuis un certain je suis tombé curieux des partitions des entiers et je n'arrive pas par exemple à bien comprendre la conversion d'un ensemble de partition d'un nombre en ensemble de somme de produits..;
Je ne trouve pas le langage conventionnel et me trouve bloqué lorsque je cherche à décrypter les formulations mathématiques.
Une approche indiquant simplement les choses en les décrivant, les nommants et éventuellement les comparant à d'autres concepts me suffirait: comprendre pourquoi n'est pas forcement une finalité pour moi.
-----