Bonjour ,
1 - Comment comprends-on les valeurs de seuils suivantes en télécom :
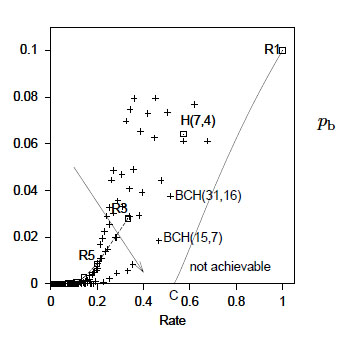
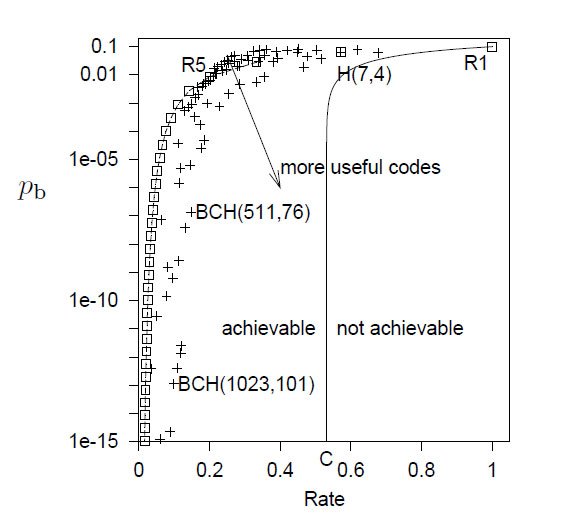
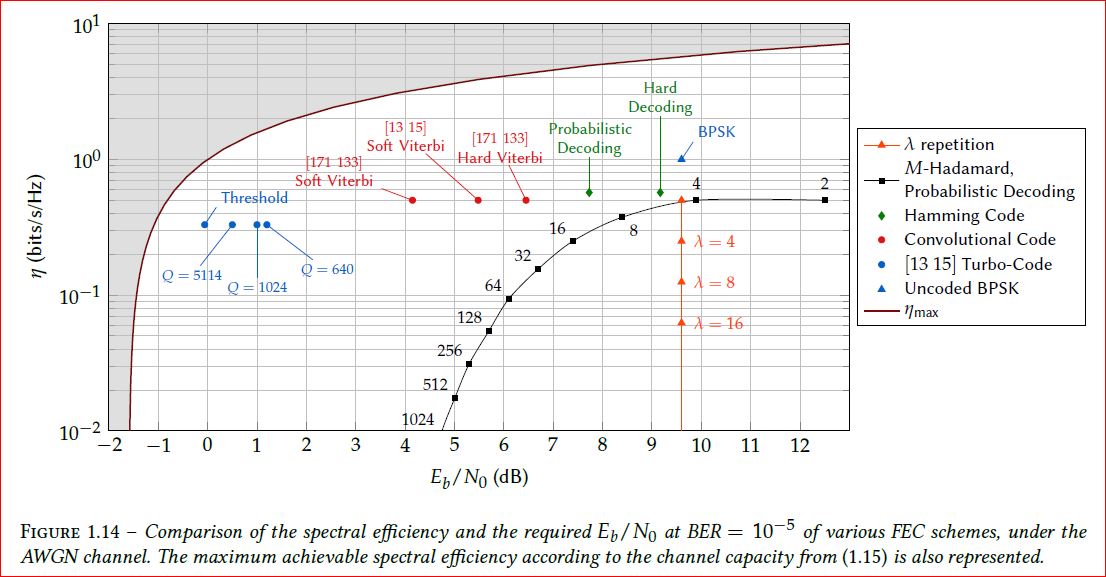
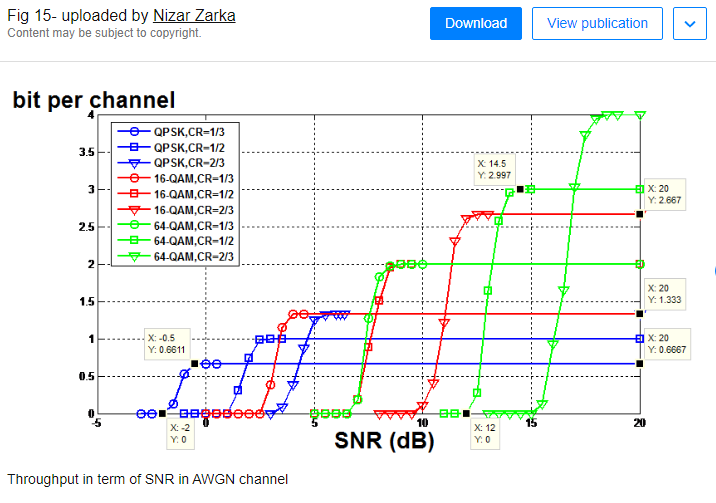
par exemple 10exposant -6 d'erreurs
que cela veut-il dire concrètement ?
pour moi c'est 1/1000000 donc : c'est une trame erronée sur 1 million de trames non érronés ?
comment détecte-on cette trame la ?
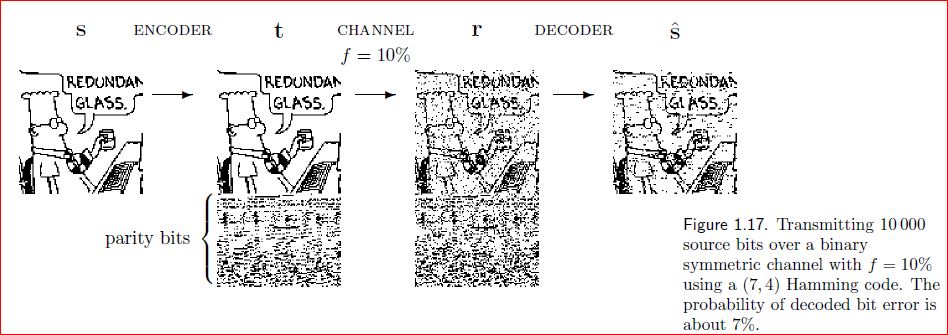
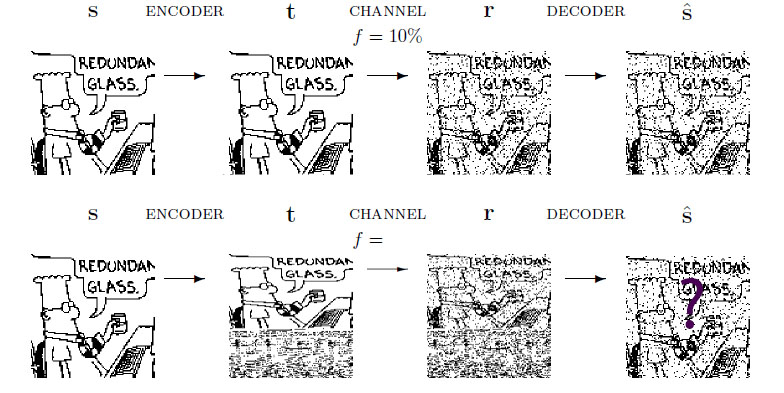
2 - la FEC (Forward error correction) : il corrige la trame elle même ? ou bien la prochaine trame (t+1) ? je me trompe ?
merci
Bonsoir,
Pour la Q1 vérifie bien le contexte car normalement un taux d'erreur est exprimé au niveau bit (Bit Error Rate), et non trame (Frame Erasure Rate pour la voix), à distinguer aussi du niveau "paquet" (Packet Error Ratio).
https://www.wikiwand.com/en/Bit_error_rate
Pour la Q2, oui le FEC concerne la correction de la trame courante (ou bloc, ou message etc...), elle nécessite une forme de redondance construite par l'émetteur qui permet au récepteur de retrouver les bit erronées et de les corriger à la volée (dans certaines conditions bien sûr).
https://en.wikipedia.org/wiki/Error_...ror_correction
cdlt,
GBo
Merci , mais ce que je ne comprends pas , comment le recepteur va reconstruire une trame avec le FEC alors qu'il l'a déja été recue ?? il y aura dans ce cas la 2 trames ?
et la détection des erreurs se fait à la réception car ça me parait logique ,
Bonjour,
C'est grâce à la redondance que cela est possible. Ce n'est pas le message tel quel qui est émis, mais davantage, sans que cela soit une "bête" répétition.
Il y a donc un cout à la méthode, on envoie plus de bits que le nombre de bits du seul message. Je vais voir si je trouve un exemple.
Voilà, l'exemple simple auquel je pensais est dans les pages 9 à 13 de cet excellent bouquin (en anglais) libre de consultation en ligne:
https://www.inference.org.uk/itprnn/book.pdf
Il s'agit du Code de Hamming (7,4) :
- aux 4 bits du message que tu veux transmettre, l'émetteur rajoute 3 bits dits "de parité" pour la redondance, calculés comme expliqué dans le bouquin
- puis il envoie les 7 bits dans un canal bruité
- le récepteur arrive à corriger UNE erreur binaire, où qu'elle soit dans les 7 bits reçus
C'est un exemple parmi d'autres de redondance utilisée pour le FEC (= permettant une certaine capacité de correction à l'arrivée sans nécessiter de retransmission), il existe des codages plus sioux bien sûr, tous inventés au 20ime siècle.
Par exemple, pour affronter le lien radio des téléphones cellulaires :
La 2G utilise du codage convolutionnel
La 3G et 4G utilisent le "Turbo code" (cocorico)
La 5G du LDPC etc...
cdlt,
GBo
Dernière modification par GBo ; 03/11/2020 à 11h17.
En 5G, il y aussi le polar code (mais que pour la signalisation) ça c'est une invention du 21ieme siècle, pardon monsieur Arıkan.
https://en.wikipedia.org/wiki/Erdal_Ar%C4%B1kan
Salut
C'est le CRC4 .On calcule la qualité de la ligne.Un nombre élévé de crc4 ralenti la transmision et decroche au bout d'un moment
ce n'est pas tres important en datas,mais en voix,c'est primordial,car la voix c'est dynamique et si on reconstitut les paquets voix ca devient inaudible
Bonjour Patrick, tu crois vraiment qu'il parle de cette vieillerie de lien TDM à 2 Mbit/s (G.703/G.704/G.732) ?
En plus pas de FEC possible avec le CRC-4 (c'est juste de la détection), donc franchement je ne crois pas.
Merci en tout cas de cette madeleine de Proust (années 1990 pour moi, j'avais tous mes cheveux)
Bonsoir.
Existe t'il une loi permettant de chiffrer le gain en termes de qualité de communication dans un canal bruité.Il s'agit du Code de Hamming (7,4) :
- aux 4 bits du message que tu veux transmettre, l'émetteur rajoute 3 bits dits "de parité" pour la redondance, calculés comme expliqué dans le bouquin
- puis il envoie les 7 bits dans un canal bruité
- le récepteur arrive à corriger UNE erreur binaire, où qu'elle soit dans les 7 bits reçus
Ici, pour transmettre avec un taux d'erreur donné, il faut un débit brut multiplié par 7/4, soit 1.75, autrement dit 75% plus élevé.
Quel est le gain obtenu en termes de rapport signal sur bruit acceptable pour un taux d'erreur donné sur le message à transmettre.
Oui c'est le 2ieme théorème de Shannon, un chef-d'oeuvre, c'est l'objet chapitre 10 du bouquin plus haut:
En gros, ça dit qu'il existe des codes d'une certaine longueur qui permettent de récupérer à l'arrivée un taux d'erreur aussi faible que voulu (malgré le bruit de canal donc) tout en maintenant une capacité non nulle qui peut aller jusqu'à C.
C est indépassable par contre , ca a été prouvé de façon rigoureuse. Shannon ne décrit pas comment faire ces codes, mais une fois qu'on en construit un (comme le Turbo Code ou le LDPC cités plus haut qui sont des champions) on le compare à la limite de Shannon pour voir comment on s'en rapproche:
http://www.josephboutros.org/ldpc_vs...ng_CLfeb01.pdf
Bonsoir.
Merci GBo.
Je suppose que le C correspond à la limite de Shannon-Hartley.
On peut dire ça, bien que le C du théorème de Shannon–Hartley est un cas particulier de capacité d'un canal continu et AWGN (voir le chap. 11 du bouquin), alors que le C du théorème au-dessus est pour un canal discret.
Dernière modification par GBo ; 04/11/2020 à 21h34.
En pratique (sur la papier en tout cas), voilà que donne le 2ième théorème de Shannon appliqué à des codes correcteurs d'erreurs classiques, donc le Hamming(7,4) vu plus haut, codes qui permettent de récupérer des erreurs après passage par un modèle de canal bruité le plus simple possible : le canal binaire symétrique. Ce canal à la propriété de faire des erreurs binaires (donc une inversion de 0 en 1 ou de 1 en 0) avec une probabilité de f.
Dans le schéma suivant, on a pris f = 0.1 :
Le schéma ci-dessus présente la probabilité d'erreur "pb" après décodage en fonction du débit utile R (normalisé à 1).
R1 = il n'y a pas de codage ni décodage, le débit est maximal mais la probabilité d'erreur résiduelle est celle du canal, donc très forte: 0.1
R3 = c'est une répétition du message suivi (ou entrelacé) de 2 copies identiques, c'est une forme de codage rudimentaire dont le décodage consiste à faire un vote majoritaire. Le débit utile est catastrophique, puisqu'on le divise par 3, mais on arrive à abaisser la proba d'erreur après décodage à 0.03, on fait donc mieux que Hamming, mais à un cout en débit plutôt rédhibitoire.
Les codes BCH sont plus sophistiqués, on y gagne sur tous les plans : moins de réduction de débit et meilleure capacité de correction.
On est cependant encore loin de la limite de Shannon qui est symbolisée par la ligne oblique qui relie C à R1 (à droite de cette ligne : zone impossible).
Sur l'axe des abscisses (le débit), C est la capacité que l'on peut espérer atteindre au maximum (pour ce type de canal) par un code correcteur et décodeur idoine avec une proba d'erreur résiduelle aussi basse que souhaitée.
Dernière modification par GBo ; 05/11/2020 à 09h00.
Re : Seuil télécom exposant / FEC
et ma question les gars !!!!
aidez moi je suis novice ..
Merci
Bonjour Linuxman,
J'ai répondu à ta Q2 dans le message #2.
Pour ta Q1, il faut que tu précises le contexte comme précisé dans le même message: bit, trame ou paquet ?
Et aussi :
De quel type de lien tu parles pour ton taux d'erreur ?
Est-ce un problème PRATIQUE (lequel ?), un exercice (quel est l'énoncé complet ?) ou une question de culture générale ?
cdlt,
GBo
Dernière modification par GBo ; 05/11/2020 à 10h26.
En attendant linuxman, pour finir sur les codes correcteurs d'erreur et le 2ieme théorème de Shannon appliqué à un canal binaire symétrique a taux de flip de 10%, voici le même graphique qu'en #13 mais avec l'axe des y gradué selon une échelle logarithmique:
Source: le bouquin cité en message #5
On reconnait R5 qui est, comme R3, un codage par "bête" répétition (R5 = 1 original et 4 répétitions), ainsi que que la courbe de ses cousins Rxx (symboles carrés) pour lesquels le débit utile s'effondre quand on vise un taux d'erreur résiduel de plus en plus faible.
Ce que je trouve fascinant dans ce théorème, c'est qu'il est contre-intuitif : on a tous l'intuition que la frontière "C" tend vers 0 quand on vise un Pb arbitrairement petit, alors qu'il est démontré mathématiquement que ce n'est pas le cas.
Dernière modification par GBo ; 06/11/2020 à 08h48.
Bonsoir.
C'est bien mon problème. Pour reprendre le code de Hamming 7/4, transmettre à un débit supérieur ( x 1.75) doit normalement conduire à obtenir un Eb/N0 des bits effectivement transmis moins bon, donc un taux d'erreur supérieur, mais la redondance a un effet plus important.Ce que je trouve fascinant dans ce théorème, c'est qu'il est contre-intuitif : on a tous l'intuition que la frontière "C" tend vers 0 quand on vise un Pb arbitrairement petit
Encore quelques heures à étudier ce que tu as transmis ... merci.
Re-, en fait je n'ai pas compris la problématique que tu exposes, pour moi le taux d'erreur est une donnée du canal, dans notre exemple "toy" au-dessus, c'est 10%.
Si on traduit ce taux d'erreur natif comme conséquence d'une valeur de Eb/N0 d'un canal réel (e.g. AWGN BPSK), ce taux d'erreur ne va pas changer en fonction du nombre de bits qu'on y fait passer.
Et en définitive, il faut rajouter des parity bits au message source si et seulement si on veut un taux d'erreur résiduel inférieur à 10% avec ce canal là, sinon on garde le débit natif (Rate = 1). C'est cette cible (le taux d'erreur résiduel voulu pour une application donnée pour un canal à taux d'erreur natif donné) qui doit guider ton choix de redondance ou pas.
Je ne sais pas si ça répond à ton interrogation.
PS : Je crois que j'ai compris ce que tu veux dire, tu voudrais "forcer" le passage des 17500 bits de t à r dans le même temps que le passage des 10000 premiers bits, c'est ça ? Si oui ça revient à changer la modulation par exemple, et ce n'est alors plus le même f, toutes choses égales par ailleurs.
Auquel cas cela reviendrait plutôt à comparer: pas de codage par canal à f% d'erreur (en haut), avec codage par canal à f'% erreur, avec f'>f.
Bonsoir.
A part "forcer", c'est presque ça.
Je me dit simplement que si je veux transmettre X bits, et que j'ai un Eb/N0 Y, alors, il va y avoir, par exemple un taux d'erreur de 10^-6.
En utilisant un code de Hamming 7/4, il est possible de diminuer le taux d'erreur, mais, pour transmettre les X bits, il faut en fait transmettre 1.75 x X bits.
Je garde le même canal, même puissance d'émission, même bande passante etc. ... (je raisonne sur un canal radio), le débit transmis dans le canal est multiplié par 1.75, et donc, l'Eb/N0 est plus bas ( Y devient Y/1.75, soit une perte de 2.43 dB), ce qui va donc occasionner un plus fort taux d'erreur sur le débit de 1.75 x X.
Mais la redondance va permettre de "rattraper" des erreurs de transmissions, et, si j'ai bien compris, le taux d'erreur sur les X bits d'origine devrait être inférieur à 10^-6.
On peut aussi faire le raisonnement à débit constant sur le canal.
J'ai un canal avec un débit de Z bits par secondes. Avec un niveau donné de Eb/N0, le taux d'erreur vaut 10^-6, ce qui va générer des retransmission de paquets et donc diminuer le débit utile. Pour pallier cet inconvénient, on utilise un codage de Hamming 7/4, mais à débit constant. Le débit utile est donc divisé par 1.75, mais avec un meilleur taux d'erreur. On espère donc que la réduction des retransmissions va compenser la perte de débit. J'imagine que dans ce cas, la manip pourrait devenir inutile au dessus d'une certaine valeur de Eb/N0.
J'ai fait le raisonnement avec le code de Hamming donné en exemple, mais, il existe peut-être de meilleurs compromis.
Désolé GBo, je n'avais pas vu ton post #21, je pianotais.
Bonsoir ! Conversation intéressante (toujours en attendant Godot), pour une fois que ça cause télécom autre que la radio pure ! je n'ai rien contre la radio hein, ami.
Oui on est d'accord, si le taux d'erreur natif de ton canal radio est 10^-6 sans codage canal (supposons du BPSK "pur"), tu auras un taux d'erreur résiduel plus petit si tu consens à rajouter de la redondance (codage canal) au message de X bits, ainsi que les opérations de décodage associées.Envoyé par Gwinver
C'est là que je décroche: si on garde le même canal (même freq. même BW, même distance émetteur-récepteur etc...), la même modulation (on reste sur BPSK donc), la même puissance radio, le même nombre d'antennes (supposons 1 antenne, du SISO quoi), comment augmenter le débit brut du canal ? Ca reviendrait à augmenter l'efficacité spectrale (en bits/s/Hz), sans rien changer ?
Oui, le Hamming a un intérêt historique surtout (et scolaire), mais le "minimum syndical" utilisé en radio, et ce dès les 1er satellites, c'est le code convolutionnel. Le GSM l'utilise aussi, avec l'algo de Viterbi pour le décodage (1967 le gars : https://ieeexplore.ieee.org/document/1054010).
cdlt,
GBo
PS : Je viens de tomber sur une thèse qui contient un schéma qui va t'intéresser je pense:
Source : https://hal.archives-ouvertes.fr/tel...794v1/document
Yoann Roth. The Physical Layer for Low Power Wide Area Networks: A Study of Combined Modulation and Coding Associated with an Iterative Receiver. Computer Science [cs]. Université Grenoble Alpes, 2017. English. fftel-01568794v1f
Dernière modification par GBo ; 08/11/2020 à 20h21.
Commentaires sur ce graphe ci-dessus:
- L'auteur a fixé le taux d'erreur résiduel souhaité à 10^-5
- le canal radio est simulé par un canal AWGN, c'est à dire à bruit blanc gaussien (qui est assez réaliste en radio, lorsqu'on veut négliger les autres impairments)
- pour chaque FEC d'intérêt (codage/décodage canal bien connus), il calcule par simulation où se situe le point de fonctionnement dans un plan [efficacité spectrale] vs. [Eb/N0] (les définitions sont détaillées dans la thèse)
- la modulation utilisée à chaque fois est BPSK, pour que l'impact seul du FEC soit mis en évidence (il n'y a pas non plus de répétitions BEC, attention)
- le point "BPSK" est la modulation sans aucun codage canal, ici il faut donc un Eb/N0 d'environ 9.7 dB pour attendre le taux d'erreur natif de 10^-5 avec ce type de canal, et ceci correspond à une efficacité spectrale de 1 bit/s/Hz.
- Avec un hard Viterbi (comme en GSM), il suffit d'un Eb/N0 de 6.4 dB pour attendre le taux d'erreur souhaité de 10^-5 : certes cela fait chuter l'efficacité spectrale à 0.5 (on divise par 2 le débit utile), mais c'est pour gagner plus de 3 dB en Eb/N0, ce qui se traduit soit en couverture radio, soit en efficacité énergétique).
- la partie grise est la zone impossible de Shannon (2ime théorème vu au-dessus), jamais violée à ce jour...
Dernière modification par JPL ; 08/11/2020 à 23h14. Motif: corrigé à la demande de GBo
Pardon remplacer 10^-6 par 10^-5 partout dans le message #25, j'ai la vue qui baisse.
C’est fait.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
Bonsoir.
ben, il faut vivre avec son temps.autre que la radio pure
sans radio, pas de sans fil.je n'ai rien contre la radio hein, ami.
Bon passons aux choses sérieuses, globalement, je cherche à évaluer le bénéfice de la redondance.
Mais, en même temps le débit utile est réduit.Oui on est d'accord, si le taux d'erreur natif de ton canal radio est 10^-6 sans codage canal (supposons du BPSK "pur"), tu auras un taux d'erreur résiduel plus petit si tu consens à rajouter de la redondance (codage canal) au message de X bits, ainsi que les opérations de décodage associées.
Disons que la redondance multiplie le débit par X.
La question est donc la suivante, est-ce que l'ajout de la redondance est bénéfique. Logiquement oui puisque c'est quasiment universellement utilisé, mais j'aimerais voir comment.Sans redondance, on a un certain Eb/N0 et donc un certain taux d'erreur.Il y a donc deux choix d' architecture du système pour atteindre un taux d'erreur donné, à débit utile constant:
Avec la redondance et les même conditions de canal, le débit utile est divisé par X, mais le taux d'erreur est plus bas.
On peut aussi choisir de réduire le débit, sans utiliser de redondance. L'efficacité spectrale sur le canal est plus faible puisque le débit est plus faible, et donc le Eb/N0 est plus favorable et le taux d'erreur est plus bas.Transmettre un débit sur le canal plus élevé en ajoutant la redondance, le Eb/N0 est moins bon, le taux d'erreur de l'ensemble utile + redondance est moins bon (taux d'erreur qui affecte l'utile et le redondant), mais la redondance permet de diminuer le taux d'erreur de l'utile.J'imagine que le choix puisse dépendre du taux d'erreur recherché, et éventuellement du type de constellation utilisée.
Rester avec ce débit utile sans ajouter de la redondance, le Eb/N0 est meilleur que pour l'ensemble utile +redondance et donc le taux d'erreur aussi.
En BPSK, par exemple, augmenter le débit signifie augmenter le symbol rate.
En QAM, les degrés de libertés permettent de changer le nombre de points de la constellation à symbol rate constant.
C'est probablement en faisant ce genre d'exercice que le 3GPP a choisi les conditions de modulation en fonction du C/N pour le LTE:
Bonjour Gwinver,
L'ajout de redondance ne multiplie pas le débit par X, ça ne se passe pas comme ça: pour multiplier le débit par X, il faut changer de modulation (en LTE : passer de QPSK à 16-QAM, ou de 16-QAM à 64-QAM), c'est pour ça que j'ai partagé un graphique au post #24 qui montre les effets du codage canal seul, à modulation constante, et cible de BER résiduel constante.
L'effet est très net : l'ajout de redondance permet de gagner en couverture radio, sans perdre en qualité de communication (puisque BER résiduel constant). Au prix d'une diminution de débit certes, mais bien moindre que ce qu'on aurait eu avec une répétition naïve.
C'est grâce au codage canal que l'on peut faire des communications intelligibles à 10 voire 20 km d'une antenne relais de 40W. Sans ça, pas de comm.
Dernière modification par GBo ; 09/11/2020 à 09h26.
Au fait merci à JPL
Ce matin j'étais à la bourre, je continue à répondre à Gwinver:
Alors justement, le LTE est un excellent exemple pour discuter sur un cas concret, on va se focaliser sur le sens descendant (base->mobiles).
Le symbol rate est une constante en LTE: c'est 15000 symboles par seconde par sous-porteuse, la base LTE peut émettre plusieurs centaines de sous-porteuses en parallèle sur le principe de l'OFDM (tout un sujet à lui tout seul...)
Comme tu le sais (je le rappelle pour les autres lecteurs), il y a 3 types de modulations possibles pour le trafic utilisateur descendant en LTE :
- le QPSK, qui transporte 2 bits/symbole, la modulation la plus robuste disponible
- le 16-QAM, qui transporte 4 bits/symbole, qui est utilisable quand les conditions radio sont bonnes
- le 64-QAM, qui transporte 6 bits/symbole qui est utilisable quand les conditions radio sont parfaites (mobile proche de l'antenne-relais)
Pour chaque type de modulation, il y a plusieurs façons d'organiser la redondance, en en mettant plus ou moins (redondance = codage canal = FEC = coding scheme...).
Ce mix de modulation et de redondance s'appelle les MCS (Modulation & Coding Schemes).
Donc, pour un nombre de sous-porteuses dédiées à une communication base->mobile particulière (par exemple sur 24 sous-porteuses), en imaginant le mobile seul dans la cellule, on ne peut augmenter son débit utile que de deux façons différentes, comme on le voit très bien dans ton graphique:
- au sein d'une modulation donnée, en réduisant la part de la redondance
- en changeant de modulation, par exemple en passant d'un MCS 16-QAM à un MCS 64-QAM si les conditions radio s'améliorent.
Tout l'art du logiciel est de choisir le bon MCS au bon moment en fonction des conditions radios qui règnent entre la base et le mobile.
C'est un peu simplifié mais voilà de quoi clarifier j'espère.
cdlt,
GBo
Dernière modification par GBo ; 09/11/2020 à 18h50.
