Discussions similaires
-
Inégalité
Par invitee791e02a dans le forum Mathématiques du supérieurRéponses: 1Dernier message: 08/03/2011, 18h02 -
Inégalité
Par inviteec33ac08 dans le forum Mathématiques du supérieurRéponses: 3Dernier message: 25/09/2010, 10h27 -
Inégalité
Par invitebeff2f95 dans le forum Mathématiques du collège et du lycéeRéponses: 3Dernier message: 24/09/2010, 17h45 -
Inégalité M
Par invite3240c37d dans le forum Mathématiques du supérieurRéponses: 2Dernier message: 24/09/2010, 03h50 -
Inégalité
Par invitecf153f02 dans le forum Mathématiques du collège et du lycéeRéponses: 2Dernier message: 28/07/2009, 12h47




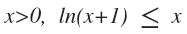 ?
?
