Calculer la coordonée Y d'un point projeté depuis un plan horizontal sur un plan oblique

[invite36602837]

Bonjour,

J'ai un problème géométrique précis, lié à de la programmation 3D DirectX, mais je n'arrive pas à trouver une réponse mathématique clair que je puisse adapter à mon cas. Et en plus je suis une brèle en math et geom !!! Je poste dans le forum math car c'est avant tout un problème de math.

Voici mon problème :
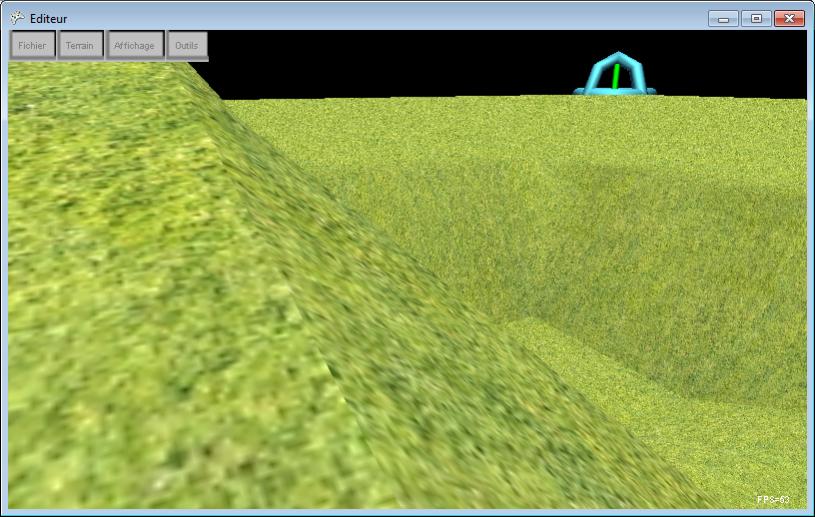
Afin de suivre un terrain en 3D, je cherche à déterminer la valeur "altitude" d'un point sur un plan oblique par rapport à un point depuis un plan de référence horizontale.

- Mon système de repère DirectX est X=latéral, Y= hauteur, Z= profondeur.
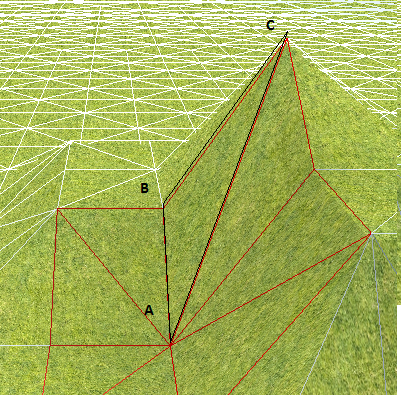
- J'ai 2 plans (P1 et P2), déterminé chacun par un triangle dont je connais précisément les 3 sommets en XYZ. (P1, P2 = triangle (Axyz, Bxyz, Cxyz))
- Un plan est parfaitement horizontale (Y=0), l'autre oblique dans un espace 3D.

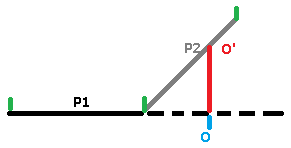
Je voudrais connaitre la coordonnée Y (qui représente l'altitude de mon points) d'un point projeter sur un plan oblique (O') à partir d un point depuis un plan horizontal (O) dont je détermine les coordonnées X et Z arbitrairement.

J'ai trouvé comment calculer la distance entre 1 plan et 1 point, mais je dois utiliser la normal du plan oblique et malheureusement la distance obtenu étant perpendiculaire au plan oblique, elle ne correspond pas à la coordonnée Y.

J'ai joint un schema rapide de mon problème


Merci de votre aide
-----

[Teddy-mension]

Salut !

Je vais essayer d'apporter ma petite pierre à l'édifice, à l'aide de mes jeunes connaissances lycéennes de géométrie spatiale, en attendant que quelqu'un de plus expérimenté t'apporte une réponse plus complète.

Si je comprends bien ton problème, tu connais les coordonnées du point (qui sont disons ), projeté orthogonal de sur le plan . Tu cherches donc l'ordonnée de ton point .

Pour cela, tu peux commencer par définir l'équation de la droite perpendiculaire au plan et passant par (appelons-la ).
Tu connais un vecteur normal à ce plan, disons (j'ai pris le plus simple, y'en a une infinité), et donc directeur de ta droite . Tu sais aussi que passe par
Une équation paramétrique de est donc :

Il faut maintenant trouver les coordonnées du point d'intersection de ta droite et de ton plan . Or, tu connais l'équation (cartésienne, je l'espère) de ce dernier.
Il suffit alors de résoudre le système de 4 équations à 4 inconnues, et de trouver le "Y" qui t'intéresse..

J'ai essayé de vous apporter une réponse, j'espère avoir bien compris votre problème, et ne pas avoir répondu à côté..
En attendant, je vous souhaite bon travail !

Teddy.

[invite36602837]

Tout d'abord merci de votre réponse. Malheureusement je me suis perdu dans la terminologie mathématique (je suis vraiment mais vraiment une brèle en math ...). Vous m'avez perdu dès l'équation paramétrique de la droite .

Je vous propose un cas concret, basé sur des valeurs pratique afin que je comprenne bien comment résoudre mon problème, et j'y joint une image du cas concret pour plus de clarté.



Je connais les coordonnées X,Y,Z des 3 sommets du triangle noir. En l’occurrence
A : X= 14.5; Y= 0.0; Z= 13.5
B : X= 14.5; Y= 0.4; Z= 14.0
C : X= 14.0; Y= 1.2; Z= 14.0

Mon point O (invisible puisque masqué par la face) est aux coordonnées :
X= 14.31; Y= 0; Z= 13.85

La normal de mon plan horizontale est
X=0,Y=1,Z=0

Donc d'après ma compréhension, limitée, la normal de mon plan horizontal au point O est
X= 14.31; Y= 1; Z= 13.85
En gros, le vecteur vertical X=0,Y=1,Z=0, translater horizontalement au point O

Mon plan oblique a pour valeur (le plan défini par le triangle noir, dont les valeurs on été générée par la bibliothèque graphique, à partir des sommets de mon triangle)
D: 6.05057859
Normal: {X:-0,78072 Y:-0,4879501 Z:0,3903601}

Mon problème étant d’exploiter correctement toutes ces valeurs, et là je m'y perd totalement.

J'abuse et j'en demande beaucoup mais pouvez vous m’écrire les 4 équations correspondant à ce cas pratique ??

[Teddy-mension]

Re-bonsoir !

Ah oui, désolé, je savais pas du tout où vous en étiez concernant les maths. ^^'

Du coup, avant d'essayer de vous répondre, je voudrais vous poser deux trois questions :

Je connais les coordonnées X,Y,Z des 3 sommets du triangle noir. En l’occurrence
A : X= 14.5; Y= 0.0; Z= 13.5
B : X= 14.5; Y= 0.4; Z= 14.0
C : X= 14.0; Y= 1.2; Z= 14.0

J'imagine que ce sont les trois points non alignés de votre plan oblique ? EDIT : Ah, en effet, votre image n'était pas encore validée quand j'ai commencé à écrire.

La normal de mon plan horizontale est
X=0,Y=1,Z=0

Là je comprends pas vraiment.. Par "La normale", vous signifiez un vecteur, une droite ? Si c'est un vecteur, il n'y en a pas qu'un, mais une infinité.. Et ici en l’occurrence, ce sont bien les coordonnées d'un potentiel vecteur normal au plan horizontal.

Donc d'après ma compréhension, limitée, la normal de mon plan horizontal au point O est
X= 14.31; Y= 1; Z= 13.85
En gros, le vecteur vertical X=0,Y=1,Z=0, translater horizontalement au point O

Même question, qu'entendez-vous par "la normale" ici ? Par ailleurs, on peut faire une translation de vecteur d'un point ou d'un ensemble de points, mais pas une "translation d'un vecteur", puisqu'un vecteur n'a pas de "position" à la base.. (?)

Bref, je passe aux équations dans le message suivant !

[A voir en vidéo sur Futura]

[Teddy-mension]

Alors, on commence par définir l'équation de la droite passant par et qui est perpendiculaire à votre plan horizontal.

* On sait que le vecteur est un vecteur normal à ce plan (on pourrait prendre , mais aussi , etc). Il est donc directeur de cette droite perpendiculaire ("Il indique sa direction").
* On sait que la droite passe par O.

Petit rappel théorique :
Une équation paramétrique (dans l'espace) d'une droite de vecteur directeur et passant par le point est :

avec (tout à l'heure j'avais mis , mais c'est bien hein)
(Pfiou, qu'est-ce que je galère à mettre ces systèmes en LaTeX..)
Ici, ton paramètre est , il peut prendre n'importe quelle valeur réelle, et il on remarque qu'il "définit" les coordonnées de chacun des points sur cette droite.

Je reviens à mes moutons. On applique tout ça à la droite qui nous intéresse, on l'a appelée , et on a l'équation paramétrique suivante :

 Cliquez pour afficher

avec
(Ici c'est T votre paramètre)

Bon, maintenant, il faut déterminer l'intersection de la droite avec le plan oblique. Ce sera le point .
Or, on connait un vecteur normal à ce plan oblique (enfin, si j'ai bien compris ce que vous m'avez dit !), appelons le , de coordonnées donc et un point de ce plan, choisissons (on aurait pu prendre ou ), de coordonnées .

Deuxième petit rappel théorique :
Une équation cartésienne d'un plan qui admet pour vecteur normal peut s'écrire sous la forme suivante :

se calcule alors à l'aide d'un point du plan. Soit un point de ce plan. On a alors:
,
d'où
Une équation cartésienne (un peu barbare ici, je le reconnais), est donc :


Pareil, on applique la chose à notre situation, et on a l'équation du plan oblique suivante :

 Cliquez pour afficher

Pour trouver les coordonnées du point d'intersection (ici, c'est hein), il ne nous reste donc plus qu'à résoudre le système d'équations (assez dégueulasse) suivant :

 Cliquez pour afficher

Et on en déduit les coordonnées de :

 Cliquez pour afficher

En fait, on connait déjà et , il ne nous reste plus qu'à calculer (donc !), qui est bien l'ordonnée du point . Et avec une méthode de substitution, on obtient:

 Cliquez pour afficher

Ce qui semble plutôt cohérent, enfin je crois. En espérant avoir été clair est bien dans le sujet, je suis prêt à répondre à vos questions !

Cordialement.

PS : Si gg0, PlaneteF ou je-ne-sais-quel membre se ramène me disant qu'il y avait une méthode beaucoup plus rapide, je cours acheter une corde et un tabouret aussitôt.

[invite36602837]

Re-bonsoir !

Ah oui, désolé, je savais pas du tout où vous en étiez concernant les maths. ^^'

Oui, niveau même pas lycée, c'est tout mon problème en fait. Je suis très bon en programmation, mais dès qu'il s'agit d'appliquer des formules de math pur, je sèche. Et d'ailleurs je tiens a vous remercier du temps que vous prenez pour m'aider.

Je précise tout de meme que d'un point de vue technique mon programme repose sur XNA/DirectX, un ensemble de fonction fournit par Microsoft pour le jeu video sur Windows, et que j'utilise les structures mathematique et les fonctions pré-programmées, en particulier la structure "Vector3" (http://msdn.microsoft.com/en-us/libr...3_members.aspx)

Là je comprends pas vraiment.. Par "La normale", vous signifiez un vecteur, une droite ? Si c'est un vecteur, il n'y en a pas qu'un, mais une infinité.. Et ici en l’occurrence, ce sont bien les coordonnées d'un potentiel vecteur normal au plan horizontal.

Cet ensemble de 3 valeurs m'est retourné lorsque j'applique la fonction pré-programmé "normalize" a mon objet vecteur. Et je comprend bien qu'il y a une infinité de vecteurs sur mon plan, puisque tout point de mon plan est défini par un vecteur. Et que je peux normalisé n'importe lequel, j'obtiendrais tjs (0,1,0). Je sais pas si je suis clair, mais le concept je le comprend bien.

Même question, qu'entendez-vous par "la normale" ici ? Par ailleurs, on peut faire une translation de vecteur d'un point ou d'un ensemble de points, mais pas une "translation d'un vecteur", puisqu'un vecteur n'a pas de "position" à la base.. (?)

Il s'agit d'une erreur de ma part. Ce n'est effectivement pas un vecteur normalisé. D'ailleurs le vecteur en question (X = 14.31; Y= 1; Z= 13.85) n'appartient même pas au plan horizontale (a cause de la coordonnée Y=1).

Bref, je passe aux équations dans le message suivant !

Va falloir que je m'accroche

[invite36602837]

Tout d'abord avec les valeurs tout est devenu limpide.

Alors, on commence par définir l'équation de la droite passant par et qui est perpendiculaire à votre plan horizontal.

Je suis parfaitement votre logique

* On sait que le vecteur est un vecteur normal à ce plan (on pourrait prendre , mais aussi , etc). Il est donc directeur de cette droite perpendiculaire ("Il indique sa direction").
* On sait que la droite passe par O.

Je suis tjs

Petit rappel théorique :
Une équation paramétrique (dans l'espace) d'une droite de vecteur directeur et passant par le point est :

avec (tout à l'heure j'avais mis , mais c'est bien hein)
(Pfiou, qu'est-ce que je galère à mettre ces systèmes en LaTeX..)
Ici, ton paramètre est , il peut prendre n'importe quelle valeur réelle, et il on remarque qu'il "définit" les coordonnées de chacun des points sur cette droite.

Là j'ai compris à quoi correspondait chaque "variable". Et surtout ou était "codé" mes coordonnées x,y,z finale (celle du point O'). En l’occurrence dans la variable "t" de chaque équation.

Bon, maintenant, il faut déterminer l'intersection de la droite avec le plan oblique. Ce sera le point .
Or, on connait un vecteur normal à ce plan oblique (enfin, si j'ai bien compris ce que vous m'avez dit !), appelons le , de coordonnées donc et un point de ce plan, choisissons (on aurait pu prendre ou ), de coordonnées .

Oui la normal du plan est bien le vecteur "k". Cette valeur m'est fournit en sortie de la fonction "normalize" de l'objet XNA représentant mon plan, et qui est construit par XNA à partir des coordonnées des 3 sommets. D’où mon problème de compréhension, je sais ce que je dois donner à manger à XNA et ce qu'il me retourne, mais je sais pas comment il le fait (donc je ne savais pas comment créer l’équation de mon plan).

Deuxième petit rappel théorique :
Une équation cartésienne d'un plan qui admet pour vecteur normal peut s'écrire sous la forme suivante :

se calcule alors à l'aide d'un point du plan. Soit un point de ce plan. On a alors:
,
d'où
Une équation cartésienne (un peu barbare ici, je le reconnais), est donc :

Voilà ce qu'il fait le petit malin de XNA derrière mon dos

Là je retrouve la résolution d'une équation à une inconnue, que j'ai appris à faire à l'école. Mais un système de 4 équations à 4 inconnues je n'avais même pas abordé la question (enfin si, en généralisant la théorie d'un système de 2 équations à 2 inconnue, mais j'avais jamais compris comment ça fonctionnait ...).

En fait je n'avais pas compris qu'à la base qu'il me suffisait de remplacer les valeurs "X, Z" dans l’équation du plan "ax+by+cz+d=0" par les valeurs de ma droite et que la variable "Y" de l'équation du plan, que vous nommé T (qui est la coordonnée O'y de ma droite OO') était finalement l'inconnu que je cherchait a obtenir. Et que la valeur correspond à la hauteur a laquelle je doit placer mon objet 3D pour qu'il soit en "surface" du plan oblique, et non au dessus ou au dessous. Et ce quelque soit la "direction" de mon plan oblique

Enfin je dit "à la base", mais c'est pas si évident que cela, et au vu de l'explication ça reste tout de même pour moi des maths de haut vol. Mais mnt grâce a vous j'ai compris des choses que j'aurais dû comprendre il y a longtemps si mes profs avaient été un peu plus pédagogue et pratique.

Ce qui semble plutôt cohérent, enfin je crois. En espérant avoir été clair est bien dans le sujet, je suis prêt à répondre à vos questions !

Oui c'est tout à fait cohérent avec mon programme.

PS : Si gg0, PlaneteF ou je-ne-sais-quel membre se ramène me disant qu'il y avait une méthode beaucoup plus rapide, je cours acheter une corde et un tabouret aussitôt.

Là dans mon programme c'est très rapide et performant

Merci beaucoup, je dois dire que vous m'avez soulager d'un gros poids. J’étais bloqué avec cette histoire "d'altitude" depuis 1 semaine. Mnt lorsque mon personnage bouge, il suit le terrain et ne passe plus au travers. Et en plus mnt que j'ai une hauteur exacte, je peux calculer la pente depuis le point d'ou part le joueur et le point où il veut aller, et déterminer si la pente est franchissable.

Etant donné l'aide que vous venez de me fournir et que cela à fondamentalement débloquer mon projet, j'aimerais vous demandez de me communiquer vos prénom/nom par MP pour que je puisse vous ajoutez à la liste des contributions à mon projet. Même si ça peut paraître général comme aide, il n'en reste pas moins que vous êtes le premier, et le seul sur internet, a m'avoir permit de résoudre ce problème. Et je vous en suis reconnaissant.

[invite36602837]

Mon problème est résolu parfaitement. Et je ne perd pas de FPS. Très bonne solution, et je suis sûr que d'autres programmeur amateur comme moi seront ravis de votre solution.

Merci encore

Et voici ce que cela donne

[ansset]

Je connais les coordonnées X,Y,Z des 3 sommets du triangle noir. En l’occurrence
A : X= 14.5; Y= 0.0; Z= 13.5
B : X= 14.5; Y= 0.4; Z= 14.0
C : X= 14.0; Y= 1.2; Z= 14.0

Mon point O (invisible puisque masqué par la face) est aux coordonnées :
X= 14.31; Y= 0; Z= 13.85

La normal de mon plan horizontale est
X=0,Y=1,Z=0

Oui, il y a plus rapide.
déjà on peut prendre A comme Origine et prendre les ecarts pour B et C
d'ou
A(0;0;0)
B(0;0,4;0,5)
C(-0,5;1,2;0,5) ( je n'ai fait qu'une translation )

equation du plan ABC :
x+ay+bz+d=0
de A on tire d=0 puis avec B et C on a
0,4a+0,5b=0 et
-0,5+1,2a+0,5b=0 , on deduit
a=5/8 et b=-1/2
l'équation du plan est donc
1)x+(5/8)y-z/2=0

le point O dans le repère avec A pour origine a pour coordonnées
O(-0,19;0;0,35)
O' est à la verticale de 0 donc
O'(-0,19;h;0,35) et O' est dans le plan donc satisfait l'équation 1)

donc
-0,19+(5/8)h-0,35/2=0
on deduit
h=0,584

[invite36602837]

Alors soit j'ai pas compris la différence, soit la résolution est humainement plus rapide, car les valeurs sont plus "abordable". Mais d'un point de vue algorithmique, c'est un peu plus complexe a mettre en place

Oui, il y a plus rapide.
déjà on peut prendre A comme Origine et prendre les ecarts pour B et C
d'ou
A(0;0;0)
B(0;0,4;0,5)
C(-0,5;1,2;0,5) ( je n'ai fait qu'une translation )

Je suis entièrement d'accord. Mais la translation va consommer quelques cycle CPU pour "translater" les vecteurs.

equation du plan ABC :
x+ay+bz+d=0
de A on tire d=0 puis avec B et C on a
0,4a+0,5b=0 et
-0,5+1,2a+0,5b=0 , on deduit
a=5/8 et b=-1/2
l'équation du plan est donc
1)x+(5/8)y-z/2=0

La simplification avec le point A je la comprend, mais d'après ma compréhension elle n'est pas "généralisable".

En effet, selon la topographie de mon terrain, le point A n'est pas toujours au niveau 0, et n'est pas toujours le point le plus bas (cas d'un pic). Parfois ca sera B ou C, voir aucun des 3 s'ils sont à la même altitude (cas d'un plateau). Il faudrait donc que je compare les 3 points pour en déduire le plus bas, puis faire les translations des 2 autres points par rapport a ce point de référence, ce qui est consommateur de cycle CPU.

L'avantage que je trouve avec la solution de Teddy-mension , c'est que sa solution utilise les valeurs réelles de mes vecteurs, et que selon que mon terrain est plus haut ou plus bas que mon altitude 0, le signe du résultat sera positif ou négatif, ce qui me permet non seulement d'en déduire très rapidement la pente (en comparant avec l'altitude calculée au mouvement précédant), mais en plus d'en déduire le signe. Avec une pente positive, je limite le dénivelé admissible. Et en négatif, j'admet tous les dénivelé. Ceci pour rendre réaliste le franchissement d'obstacles.

De plus, j'ai 2 situations distinct dans mon programme:
- Suivre le terrain, comme si je marchait (mode FPS).
- Evoluer dans le volume 3D comme un avion, en évitant de passer à travers le sol (mode SIM).

Mais j'admet que votre solution est plus abordable d'un point de vue "calcul mental".

A moins que je n'est pas compris comment la généralisée (ce qui ne m'etonnerais qu'a moitié, vu mon niveau en math ...)

[ansset]

c'est totalement généralisable.
j'ai pris A parceque c'était le premier, j'aurai pu prendre n'importe quel point de repère initial.
même un point qui ne soit ni A,ni B,ni C.
ce qui permet de choisir n'importe quel point de départ.
ensuite l'équation change
il suffit de placer O dans le nouveau repère et de déduire O' de la même manière.

[invite36602837]

Ok, je comprend comment la généralisée.

L'un comme l'autre vous déterminez la hauteur a partir de l’équation du plan. Donc d'après ma compréhension mathématique, si je conserve mon point d'origine (0,0,0), votre solution est exactement la même que celle de Teddy-mension. Est-ce que je me trompe ??

----

Je pense que d'un point de vue "informatique", votre solution de déterminer un nouveau point d'origine est plus complexe et consommatrice de cycle CPU que celle de Teddy-mension,. Soit je garde mon point de repère à l'origine (0,0,0) et j'applique la solution pratique de Teddy-mension, soit je déterminer un nouveau point de repère (X,Y,Z) et j'applique votre solution.

Le critère pour choisir quelle solution est la meilleurs pour mon cas sont les performances de mon programme, car je doit maintenir un nombre d'images par seconde acceptable pour qu'il soit fluide.

Il est plus efficace informatiquement de résoudre directement une équation mathématique que de devoir créer des variables temporaire de traitement, de leur attribuer les valeurs réelles translatée par rapport à un point XYZ, et de résoudre la même équation (sans parler de la consommation mémoire, que je cherche à limiter au maximum vu que mon programme a déjà une charge de 150Mo en RAM, et ce n'est pas fini).

[Teddy-mension]

Là j'ai compris à quoi correspondait chaque "variable". Et surtout ou était "codé" mes coordonnées x,y,z finale (celle du point O'). En l’occurrence dans la variable "t" de chaque équation.

C'est ça. Généralement, pour passer d'un point à un autre sur votre droite , alors il faudra forcément ajouter dans le sens des abscisses, dans le sens des ordonnées, et dans le sens des cotes (et peut prendre n'importe quelle valeur, c'est elle qui va donc définir les coordonnées de tous les points). C'est pour ça que les coefficients devant (donc , et ) sont les coordonnées d'un vecteur directeur de .

D’où mon problème de compréhension, je sais ce que je dois donner à manger à XNA et ce qu'il me retourne, mais je sais pas comment il le fait (donc je ne savais pas comment créer l’équation de mon plan).

XNA permet donc visiblement de passer de trois points non alignés d'un plan à un vecteur normal au plan. Et c'est à l'aide de ce vecteur qu'on peut en effet trouver une équation cartésienne du plan (et d'un point du plan, bien sûr).

J'ai balancé la solution cash hier, mais je pourrais d'ailleurs un peu plus développer, ça peut toujours servir. Il faut faire appel à la notion de produit scalaire.
Petit rappel :
Le produit scalaire de deux vecteurs et est égal à .

Soit un plan, et un vecteur normal à .
Soit un point quelconque.
On a
(deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul)
(Là on applique le produit scalaire, donc)

Et en posant , on retrouve bien l'équation cartésienne de , soit :

En fait je n'avais pas compris qu'à la base qu'il me suffisait de remplacer les valeurs "X, Z" dans l’équation du plan "ax+by+cz+d=0" par les valeurs de ma droite et que la variable "Y" de l'équation du plan, que vous nommé T (qui est la coordonnée O'y de ma droite OO') était finalement l'inconnu que je cherchait a obtenir. Et que la valeur correspond à la hauteur a laquelle je doit placer mon objet 3D pour qu'il soit en "surface" du plan oblique, et non au dessus ou au dessous. Et ce quelque soit la "direction" de mon plan oblique.

En fait, ici on a un système de quatre équations à quatre inconnues extrêmement simplifié. En effet, on connait déjà deux inconnues ( et ), et les deux autres ( et ) sont égales. Du coup, il suffit de remplacer et dans l'équation qui contient à la fois , et , pour trouver .
Cependant, on a pas toujours cette chance. Si on a une équation paramétrique de plus "générale", disons :

Et que l'équation cartésienne du plan est disons
Alors le système peut se résoudre ainsi :




Ensuite, on remplace dans chaque équation, et là on a les coordonnées du point d'intersection entre le plan et la droite.

[Dernière petite parenthèse : Ces systèmes de 4 équations à 4 inconnues restent tout de même assez simples à résoudre. Les systèmes plus compliqués, sous la forme suivante (ici, les inconnues sont , , et ):

.. se résolvent à la main, notamment sous la forme matricielle, à l'aide d'un outil qui se nomme le Pivot de Gauss. C'est aussi directement faisable sur une calculatrice qui inverse directement les matrices.
Enfin bref, voilà pour les systèmes.]

Merci beaucoup, je dois dire que vous m'avez soulager d'un gros poids. J’étais bloqué avec cette histoire "d'altitude" depuis 1 semaine. Mnt lorsque mon personnage bouge, il suit le terrain et ne passe plus au travers. Et en plus mnt que j'ai une hauteur exacte, je peux calculer la pente depuis le point d'ou part le joueur et le point où il veut aller, et déterminer si la pente est franchissable.

Etant donné l'aide que vous venez de me fournir et que cela à fondamentalement débloquer mon projet, j'aimerais vous demandez de me communiquer vos prénom/nom par MP pour que je puisse vous ajoutez à la liste des contributions à mon projet. Même si ça peut paraître général comme aide, il n'en reste pas moins que vous êtes le premier, et le seul sur internet, a m'avoir permit de résoudre ce problème. Et je vous en suis reconnaissant.

Ouah ! Je suis vraiment heureux d'avoir pu être utile pour vous, et d'avoir débloqué plus ou moins votre projet.
(Vous m'avez également permis de réviser ma géométrie spatiale, que je devrais approfondir davantage cette année, et je vous remercie pour ça. ^^)

Ce que vous me demandez me touche beaucoup, et je vous envoie un MP sur le champ pour vous communiquer tout ça.
Quoiqu'il en soit, n'hésitez surtout pas à repasser sur Futura-sciences, il y aura toujours quelqu'un, que ce soit moi ou des personnes plus expérimentées (je ne suis qu'en prépa, après tout) pour vous aider. En tout cas je serais ravi de vous apporter de nouveau une quelconque aide.

Cordialement.

PS : Je me suis emmêlé les pinceaux entre tutoiement et vouvoiement au début de la discussion, veuillez m'en excuser.

EDIT : Zappage du message d'ansset !

[monoe]

Voila un cours bien détaillé comment tu peux calculer:
Cours topographie PDF et exercices corrigés

source: genie civil experts