Probléme de tyauterie

[tuyauteur]

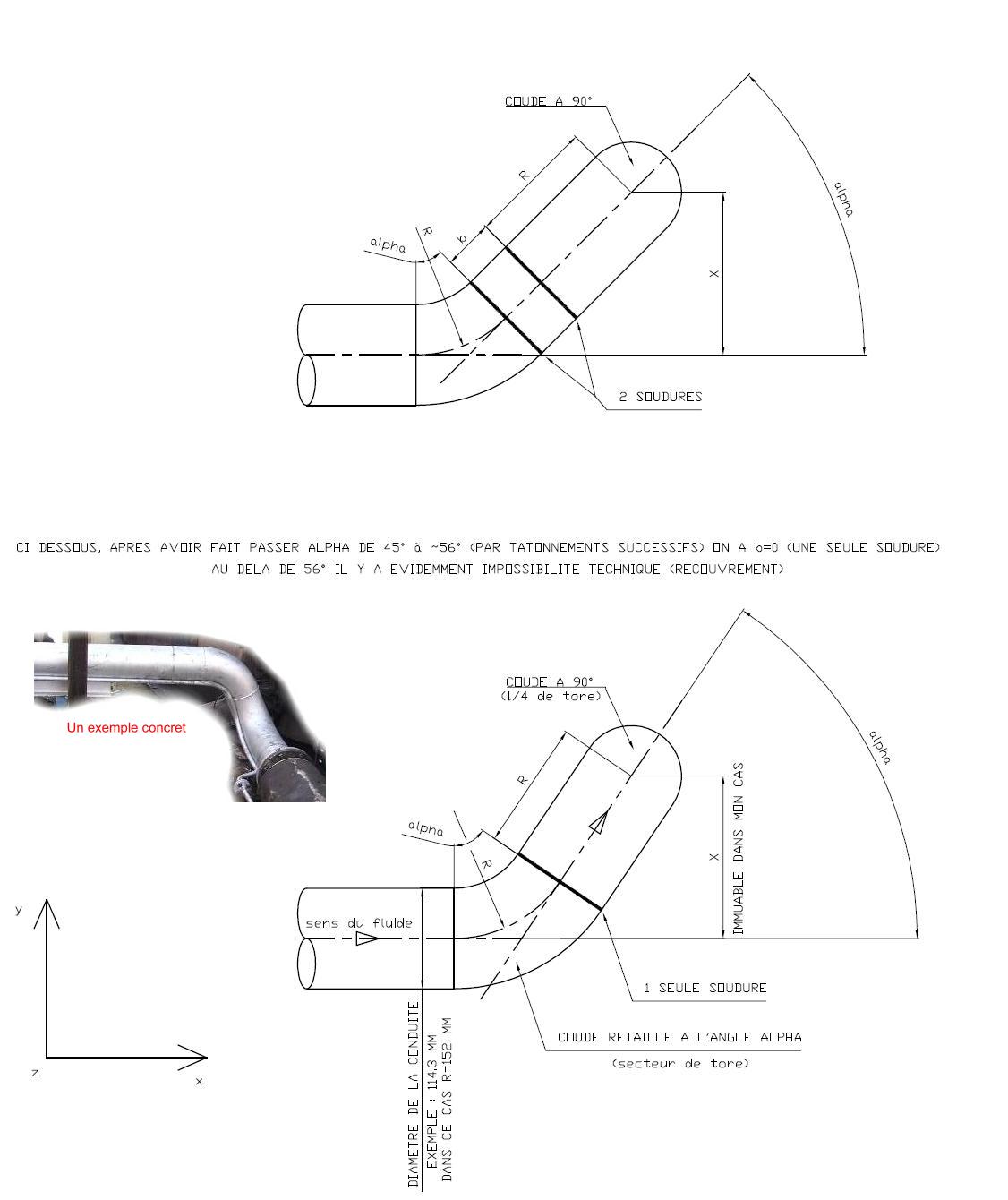
Un tuyauteur industriel doit fabriquer un tronçon de tuyauterie telle que dans le schéma ci joint, vu en plan. (vu de dessus).
Pour des raisons pratiques, il impose la cote X.
Afin de réaliser le double changement de direction de la conduite, il utilise deux coudes du commerce, de rayon R (connu), l'un à 90°, l'autre retaillé à l'angle alpha.
Afin de gagner une soudure, il veut faire varier alpha pour que b soit nul.

Comment exprimer alpha en fonction de X pour que b soit nul ?

Trop compliqué pour moi, doit y avoir une histoire de 2 équations avec 2 inconnues ou un truc comme ça (je tourne en rond).

Merci pour votre coup de main !

Pièce jointe supprimée
-----

[JPL]

Les images doivent être postées dans un format graphique (gif, png, jpg). Merci.

[tuyauteur]

Voici la pièce jointe

[gg0]

Bonjour.

Est-ce moi qui comprends mal, ou le problème est-il posé de travers ? Il y a d'abord deux soudures (pourquoi ??) puis on demande b=0 qui correspond d'après la figure à une seule.

Déjà, faire une figure avec b=0 serait une amélioration. Ensuite, il est difficile de savoir à qui correspond X, sur le schéma, il semble y avoir deux tuyaux arrivant de gauche, mais un seul à la fin. Est-ce le cas ?

Cordialement.

[A voir en vidéo sur Futura]

[WillowII]

Bonjour,

j'ai peut-être trouvé une solution mais elle suppose que le rayon du gros tuyau soit connu. Est-ce le cas ou pas?

[Dynamix]

Salut
Il n' y a qu' un tuyau , et son diamètre n' a pas d’importance .
S' il y avait 2 tuyaux il seraient séparés par un trait continu .
On peut simplifier la figure en ne gardant que l' axe .
La cote X est une valeur invariable .
En augmentant l' angle alpha , on diminue la cote b .

[gg0]

Désolé, je ne comprends plus ! Ton dessin est bizarre (à gauche) pour un seul tuyau. mais baste !

Enlève du dessin tout ce qui ne sert à rien (tuyau, les deux soudures). Donc fais la figure avec b=0.

Cordialement

[Dynamix]

Donc fais la figure avec b=0.

b = 0 , c' est le problème résolut .
Avant d' arriver au problème résolut , il faut poser b = **** et chercher à quelle condition **** est égal à zéro .

[gg0]

Rien n'interdit de faire la figure (X n'est pas relié aux autres lettres) et d'en déduire la valeur de alpha.

Il ne s'agit pas vraiment ici d'un problème de minimum. C'est un problème de détermination d'une valeur, et il est toujours plus simple de supposer le problème résolu pour trouver cette valeur.

[tuyauteur]

Bonjour,

j'ai peut-être trouvé une solution mais elle suppose que le rayon du gros tuyau soit connu. Est-ce le cas ou pas?

Merci WillowII,
Oui le Rayon est connu. Par exemple pour une conduite de diamètre 114,3 mm, le rayon du coude est de 152 mm.

[tuyauteur]

Bonjour.

Est-ce moi qui comprends mal, ou le problème est-il posé de travers ? Il y a d'abord deux soudures (pourquoi ??) puis on demande b=0 qui correspond d'après la figure à une seule.

Déjà, faire une figure avec b=0 serait une amélioration. Ensuite, il est difficile de savoir à qui correspond X, sur le schéma, il semble y avoir deux tuyaux arrivant de gauche, mais un seul à la fin. Est-ce le cas ?

Cordialement.

Merci gg0 de vous intéresser au sujet.

Il y a d'abord deux soudures car justement l'angle alpha n'est pas connu.
Il à été arbitrairement défini à 45° par exemple. Ceci génère 2 soudures car X est imposé.
En faisant varier alpha mais en conservant la cote X les 2 soudures vont se rapprocher l'une de l'autre, pour n'en former plus qu'une lorsque alpha atteindra une certaine valeur.

Pour expliquer le schéma, imaginez le en vue de dessus (Vu du ciel).
Si un fluide circule dans cette conduite, admettons de la gauche vers la droite, il va bifurquer à gauche dans le coude alpha (dans un plan parallèle au sol) puis plonger vers le sol dans le coude à 90° (qui lui est orienté selon alpha en vue en plan).

La cote X est imposée pour éviter un obstacle par exemple.
Si elle était égale à 2xR nous aurions 2 coudes à 90° (l'un tournant à plat dans un plan parallèle au sol, l'autre plongeant vers le sol dans un plan perpendiculaire au sol).

J’espère avoir été plus clair!

Merci à tous

[Dynamix]

J’espère avoir été plus clair!

Il manque le principal :
Ou en es tu ? Qu' as tu posé , écris , crobardé ...?

[tuyauteur]

Voila Dynamix, j'ai complété mon schéma:

[gg0]

Bon,

je pense avoir complètement compris ton problème. Dans ce cas, on obtient non seulement une formule exacte (c'est de la trigo de fin de collège + la fonction arcsin), mais aussi le fait qu'il y a une assez bonne approximation simple.
La formule exacte :

L'angle est en radians. En degrés (y compris la fonction arcsin que je note alors arcsin°) :


L'approximation en radians

et en degrés

L'erreur maximale, en degrés, est de 3° en plus ou en moins.

Cordialement.

[gg0]

A noter : j'ai traité le problème mathématique. les questions techniques de soudure ne me concernent pas.

[tuyauteur]

Bon,

je pense avoir complètement compris ton problème. Dans ce cas, on obtient non seulement une formule exacte (c'est de la trigo de fin de collège + la fonction arcsin), mais aussi le fait qu'il y a une assez bonne approximation simple.
La formule exacte :

L'angle est en radians. En degrés (y compris la fonction arcsin que je note alors arcsin°) :


L'approximation en radians

et en degrés

L'erreur maximale, en degrés, est de 3° en plus ou en moins.

Cordialement.

Merci beaucoup gg0,
j'ai testé avec quelques valeurs et cela fonctionne à la perfection ! (X=2R par exemple)
A mon époque je ne pense pas avoir fait de trigo au collège, je pensais l'avoir découvert au lycée.Elle était un peu loin dans tout les cas.
Encore un grand merci à tous.
Eric.