Petite question (hors programme, pour le fun!)
J'ai pris la fonction f telle que fn(x)= exp(-x^n) avec n E N. J'ai tapé après 10 fonctions, avec n=1, n=2.. jusqu'à n=10 et j'ai remarqué que pour un n pair, la fonction semble former un "rectangle" (il manque un coté) de largeur 1 et de longueur 2, avec l'axe des ordonnées comme axe de symétrie.
J'ai alors tapé la fonction f888 tel que f888(x)=exp(-x^888) et j'en conclut que ma conjecture semble vraie.
Voici la fonction en question :
Mais le problème c'est que je ne sais pas par ou commencer. J'ai posé les points A et B de coordonnées respectives (-1,1) et (1,1) ainsi que H(xA,0) J(xB,0). Je me suis dit qu'en prouvant que le produit scalaire de A avec H et B avec J serait nul j'aurai demontré l’orthogonalité et après j'aurai mesurer la longueur AB qui devrait être égale à HJ. Mais je ne connais pas n et je ne sais pas manier des calculs avec des puissances infinies (enfin je crois pas). Je me demande comme je peux déterminer n et démontrer qu'il faut qu'il soit pair pour que la fonction forme un "rectangle".
Des idées?
-----
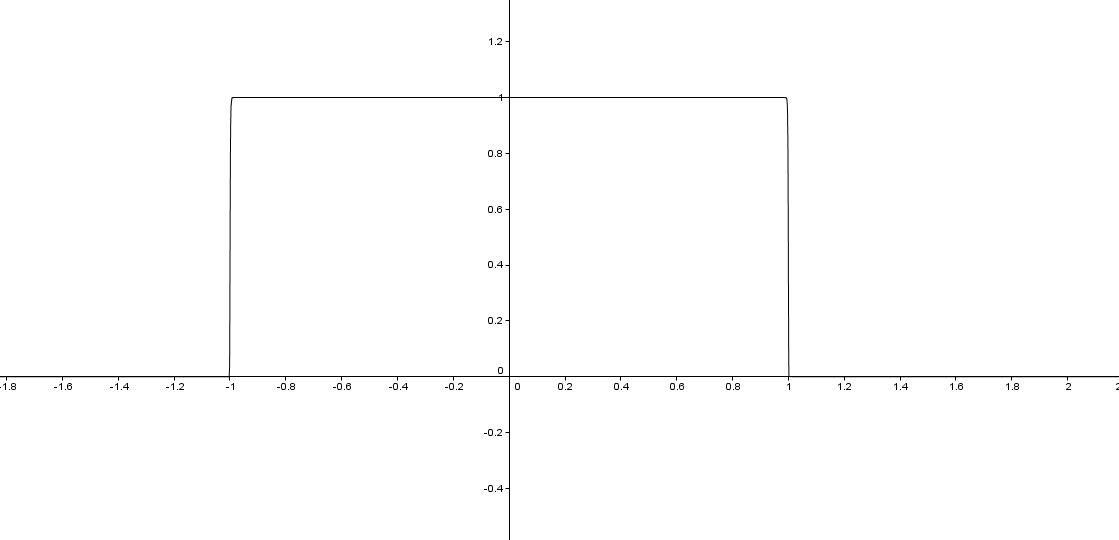
entre -1 et 1. Tu verras que pour n très grand, on est quasiment à 0 sauf très près de -1 et de 1. or exp(-0)=1, donc tes fonctions, pour n grand sont très proches de 1 de -1 à 1. Ensuite, elles ont toutes la même valeur, pour x=1, et seulement deux pour x=-1 suivant la parité de n; enfin, dès qu'on dépasse 1 ou -1, les valeurs de xn sont, en valeur absolue, très grandes, donc, pour n pair, on a une valeur très proche de 0 dès qu'on s'éloigne de -1 ou 1.