Bonjour à tous, je rencontre un problème avec l'exercice suivant:
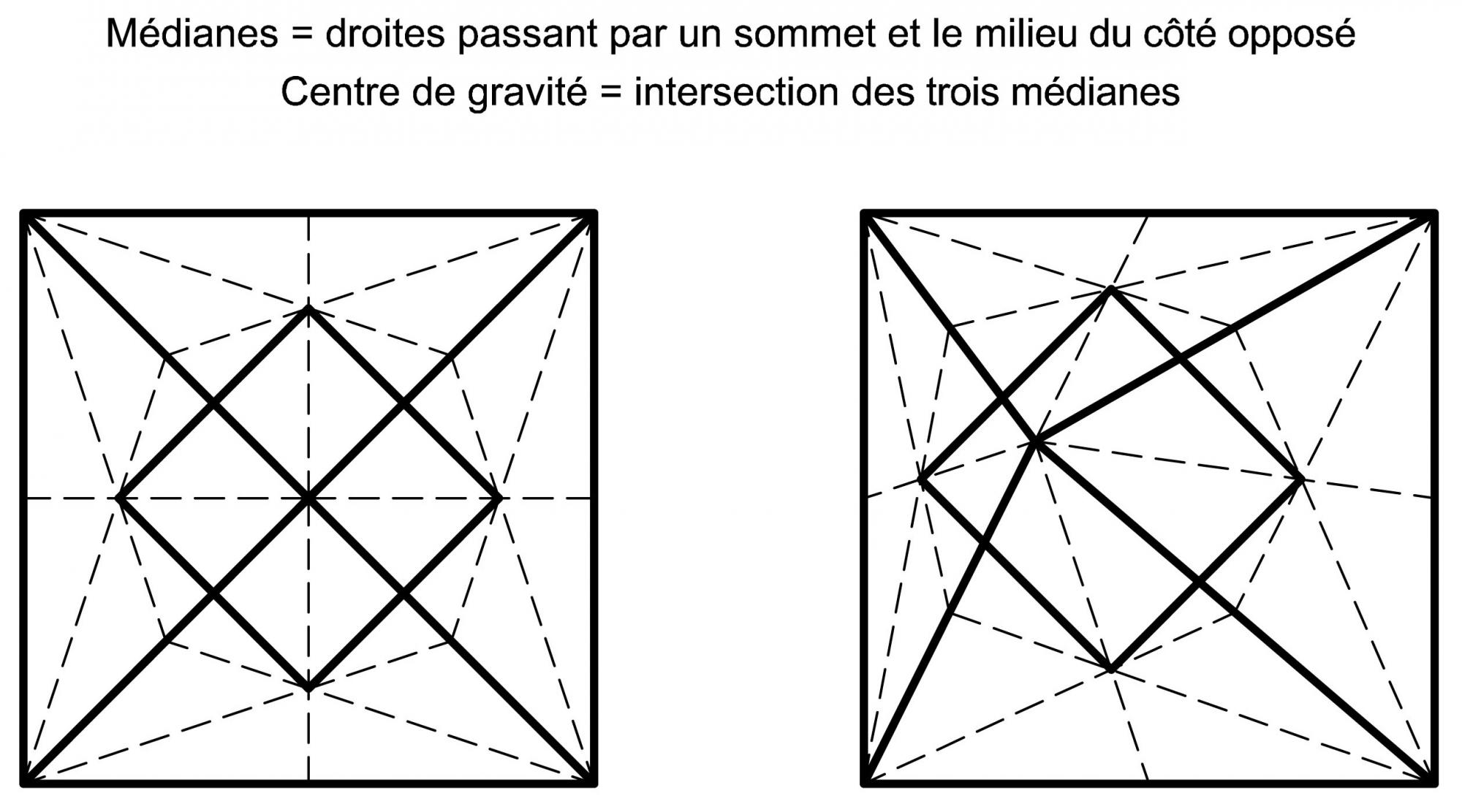
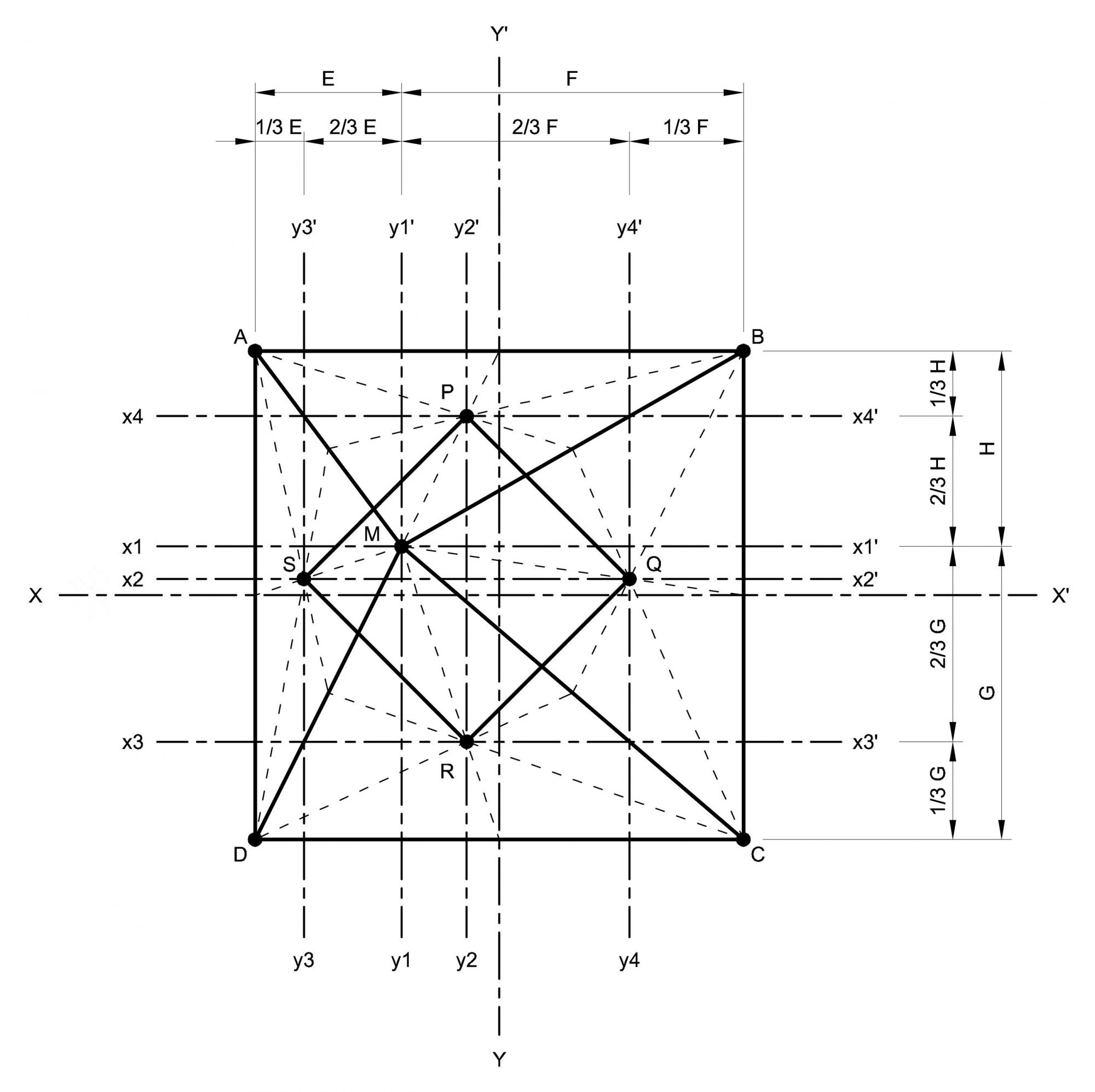
ABCD est un carré et M un point intérieure. P, Q , R et S sont les centres de gravité des triangles AMB, BMC, CMD et DMA
Montrer que PQRS est un carré.
Ca fait un bon moment que j'essaye de trouver une piste, mais sans résultat, je ne sais pas par où commencer J'espère recevoir une réponse ou une indication sur la démarche.
Merci d'avance.
Je n'ai pas le temps d'approfondir, mais perso, sachant que les centres de gravité sont sur les médianes des triangles, je commencerais par mettre en évidence le carré dont les sommets sont les milieux respectifs des côtés du carré initial, ensuite je réfléchirais.
Attention : sans garantie que ce soit la bonne piste.
On trouve des chercheurs qui cherchent ; on cherche des chercheurs qui trouvent !
Bonjour.
Problème facile à traiter en utilisant les vecteurs.
On peut exprimer les 4 vecteurs correspondant à chacun des quatre cotés du carré PQRS, en fonction par exemple de AM, AB et AD (Rappel : Si G est le barycentre de ABC et O un point quelconque, OG=(OA+OB+OC)/3)
On vérifie aisément que PQ=-RS et PS=-QR.
Ensuite, il faut vérifier que les cotés sont tous égaux, et que deux cotés adjacents sont perpendiculaires.
Mais il faut avoir déjà vu les propriétés du produit scalaire et savoir que norme =racine du produit scalaire d'un vecteur par lui-même, et produit scalaire nul si vecteurs perpendiculaires
Je ne sais pas, compte tenu des nouveaux programmes, si on apprend encore cela au Lycée.
Sinon, il faudra faire les calculs en coordonnées cartésiennes en posant M (x, y) et en calculant les coordonnées de chaque point, puis les coefficients directeurs des segments et leur longueur
Même principe, mais un peu plus laborieux
Dernière modification par Resartus ; 12/11/2016 à 10h07.
Why, sometimes I've believed as many as six impossible things before breakfast
Bonjour,
Bel exercice !
Pour la démonstration intuitive :
Dans le premier cas (point M au centre du grand carré), la raison saute aux yeux !
On a quatre triangle-rectangle, donc deux diagonales du grand carré (se croisant à angle droit) qui peuvent également être interprétées comme deux axes de symétrie… les côtés deux-à-deux (opposés) du petit carré resteront parallèles aux axes de symétries
Dans le deuxième cas (point M situé aléatoirement dans le grand carré), la raison est plus subtile.
Les quatre triangles sont interconnectés ; Autrement dit, ils dépendent les uns des autres.
Les dimensions d’un triangle détermineront les dimensions des trois autres triangles.
Ce qui implique que deux centres de gravité (deux-à-deux, horizontalement ou verticalement) se déplaceront de manière proportionnelle au sein des deux triangles opposés.
On conserve ainsi les mêmes dimensions et inclinaison du petit carré, qui se déplace "uniformément" au sein du grand carré.
Pour la démonstration mathématique… je suis curieux de voir la réponse !
Dernière modification par PPathfindeRR ; 12/11/2016 à 10h10.
« Un problème sans solutions est un problème mal posé ! » Albert Einstein.
Bonjour,Envoyé par danyvio
Pour moi, il faudrait démontrer dans un premier temps que le quadrilatère a des côtés parallèles deux à deux et ce en utilisant le fait que partout tu as des " milieux" de segments. Regarde bien la figure, les mots "milieu" et "parallèles"doivent te faire penser à un théorème précis.
Je n'ai pas encore tout essayé mais "certains matheux" du groupe présents pourront me/nous dire si je te mets sur la bonne piste
Bon courage Pernelle
Rebonjour,
Effectivement, la méthode géométrique est de loin la plus astucieuse. Le quadrilatère cherché est homothetique au carré des milieux.
(Mais j'ai de gros doutes sur le fait qu'on enseigne cela de nos jours...)
Why, sometimes I've believed as many as six impossible things before breakfast
SA+SD+SM=0 et aussi
RD+RC+RM=0 d'où
SR=SM+MR et en remplaçant
SR=AS+DS+RD+RC=AS+RC+RS d'où
SR=(AS+RC)/2
Or AS coupe DM en son milieu tout comme CR ( R et S barycentres )
si T est ce milieu on a même
AS=(2/3)AT et RC=(2/3)TC
d'où
SR=(1/2)(2/3)AC=(1/3)AC.
sachant que AC est une diagonale du carré initiale, et par toutes les symétries, on en déduit que SRQP est carré.
Re-
J’essaie de trouver des relations pour trouver la démonstration mathématique, mais j’avoue que ce n’est pas évident du tout !
Cet exercice n’est pas simple !
Je remets une image avec les repères et axes principaux :
« Un problème sans solutions est un problème mal posé ! » Albert Einstein.
il me semble que je viens de la donner, non ?
ps : j'ai bien sur tout écrit en vecteur , notamment en utilisant Chasles.
donc par exemple SA=-AS
c'est ce que je regardais.
votre message n'était pas encore affiché lorsque j'éditais mon message (malgré les 34min d'écart !), j'ai pu voir votre réponse en revenant 5min plus tard.
Dernière modification par PPathfindeRR ; 12/11/2016 à 12h21.
« Un problème sans solutions est un problème mal posé ! » Albert Einstein.
Bonjour Ansett
Il me semble qu'il faudrait savoir aussi dans quelle classe se trouve RANDOM
Si c'est en 3ème, les vecteurs ne semblent pas au programme.
Je ne connais pas encore les programmes de seconde et de 1ère
Il faudrait aussi préciser les propriétés de la médiane, que le 1/2 de la démonstration correspond à la propriété de la médiane qui joint un sommet au milieu du côté opposé dans un triangle et que le 2/3 correspond à la propriété du centre de gravité situé au 2/3 de la médiane à partir du sommet et reste donc 1/3 de la médiane entre le centre de gravité et le milieu du côté du triangle en question. Non ?
Pernelle
effectivement.
mais je ne vais pas faire de "rappel" de cours.
la démo que je propose me semblait être la plus simple, par défaut, sans effectivement savoir si l'utilisation de la relation de Chasles est "autorisée".
c'est quand même beaucoup plus simple que le graphique de PPathfindeRR.....
On y retrouve d'ailleurs que les cotés du petit carré sont parallèles aux diagonales et que les cotés mesurent 1/3 des grands cotés.
par ailleurs, je doute que cet exercice lui soit proposé en 3ème.
En tout cas, il y a certainement des choses dans ses cours qui permettent de résoudre cet exercice.
Bref, je ne comprend pas trop la remarque.
ps :random1 a 16 ans, il est très certainement au lycée et a très certainement vu les notions que j'utilise.....
Pour aider à la compréhension de la démonstration ,il est parfois nécessaire pour des "lecteurs" dont les "souvenirs" sont un peu loin,de faire un minimum de rappel de cours...en quatre lignes en ce qui me concerne...
Je pense comme vous que ce jeune doit être au lycée
Pernelle
pour te répondre , j'utilise les propriétés suivantes :
-relation de Chasles ; à savoir qu'en "vecteur"
( mais , pour un gain de temps, je n'ai pas écrit en Latex.)
-première propriété du barycentre G de 3 points A,B,C:
-autre propriété du barycentre G d'un triangle :
il est à l'intersection des médianes et si T est le milieu du coté opposé à A alors
et je n'utilise que cela.
Cdt
la seconde propriété se déduisant de la première.
Je vous remercie
Pernelle
