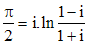Jolie formule

[XxDestroyxX]

Bonjour/Bonsoir, je crée cette discussion juste pour montrer une formule sans prétention que j'ai trouvé (qui a peut être déjà été trouvée) et personnellement, je la trouve jolie



Le rendu latex n'est pas très beau
Sinon, dites moi ce que vous en pensez et n'hésitez pas à écrire une formule jolie à votre tour !
Bonne journée/soirée
-----

[gg0]

Bonjour.

C'est peut-être joli pour toi, mais je ne sais pas ce que signifie le deuxième terme : Je connais les racines carrées, cubiques, .. de réels, mais déjà pour des réels négatifs, la notation de la racine carrée n'a pas de sens conventionnel. Alors une racine de i ??? Et une racine i-ième ???
Donc que veux-tu signifier ici ?

Autre question : Qu'appelles-tu "trouver" ?

[fartassette]

bonjour,

Je pense avoir compris cette formule !!!!! c 'est bien comme ceci que vous avez fait n 'est ce pas?

[gg0]

Pourquoi pas ?

Mais ce n'est plus une racine i-ième, et il y a utilisation de formules qui dans d'autres circonstances donnent des résultats faux.

Cordialement.

[A voir en vidéo sur Futura]

[XxDestroyxX]

J'avais fait :



En changeant juste l'un des termes de l'autre côté, ça m'a donné cette formule

gg0 : Ah bon ? ?
Dans quels contextes c'est faux ?

[Dinozzo13]

Salut !

Savoir donner un sens à (que tu notes ), cela revient à donner un sens à , c'est-à-dire . Or pour donner du sens à , il faut passer par le logarithme en écrivant que . Mais peut avoir plusieurs sens suivant la détermination du logarithme que l'on prend. Sans entrer dans les détails, peut valoir , mais peut également valoir par exemple. Cela vient du fait que "formellement", on a , mais pas pour tout complexe z, il faut retirer une demi-droite d'origine O.

[eudea-panjclinne]

Bonne curiosité XxDestroyxX ! C'est le comte Giulio Carlo Di Fagnano qui au début du 18e siècle avait exhibé sans démonstration un certain nombre de formules de ce type. Ce qui avait grandement excité la curiosité des milieux mathématiques et accru le regain d’intérêt pour les nombres complexes qui restaient peu employés à l'époque car on ne les comprenait pas bien. Ce fut aussi à l'origine de la controverse entre D'alembert et Euler (*) sur le sens à donner à certain logarithme tels ln(-1). Les problèmes de ce genre de relations, évoqués par les intervenants précédents, ont été résolus au 19e siècle avec la théorie des fonctions de variable complexe et l'introduction des surfaces de Riemann.

(*) Controverse sur le logarithme

[gg0]

Ce qui fait que cette "jolie formule" n'est ni vraie ni fausse, et surtout, inutilisable sauf dans un contexte très particulier, annoncé à l'avance.

[gg0]

Pour , il manque une définition de la signification du radical pour des nombres autres que des réels et des "exposants de radical" autres que des entiers positifs.
Déjà le choix entre et pour pose problème !!! (*)
Tu as choisi une traduction pour une notation qui n'est jamais utilisée par les mathématiciens, faute d'intérêt.

Deuxième problème : la formule que tu utilises à la deuxième étape n'est pas généralisable aux complexes (elle donne des calculs faux, ça revient souvent sur les forums).

Donc une notation inutile + un calcul non justifiable = une formule qui n'est pas des maths (actuelles).
Mais c'est "joli" !

Cordialement.

(*) il peut être utile de revenir à la définition de la racine carrée.

[XxDestroyxX]

Merci à tous pour vos réponses constructives, l'ensemble des complexes est vraiment complexe pour le coup ! Par ailleurs, n'hésitez pas à partager vos formules préférées (dont je ne connais sûrement pas l'existence), ça permettrait à tous ceux que ça intéresse d'étendre leur culture mathématique !

[fartassette]

,

Salut !
. Sans entrer dans les détails, peut valoir , mais peut également valoir par exemple. Cela vient du fait que "formellement", on a , mais pas pour tout complexe z, il faut retirer une demi-droite d'origine O.

Bonsoir,

j 'ai essayé de retrouver la formule qui permet de traiter les logarithmes des nombres négatifs et imaginaires à l 'aide d 'un plan complexe. Comme il existe une infinité d 'angles dont les sinus et cosinus sont donnés on pourrait aisément en obtenir une formule générale.

Donc d'après un dessin, le z peut s 'écrire:



ce qui revient à en appliquant le logarithme on a bien


pour l’exemple on a


or,


d'ou avec


Sauf erreur bien sûr

[V13]

C'est la formule la plus proche de ce que vous avez trouvé