Distance orthodromique et loxodromique (question!).

[1max2]

Bonjour à tous, j' ai une petite question (ça n'est pas un problème à faire, c'est juste pour le "fun" ! )
Un gars me demande de lui expliquer sans trop de math pourquoi la distance orthodromique est plus courte que la distance loxodromique.Voilà comment je lui ai expliqué :
D' après ce que j' ai compris donc, pour avoir la distance la plus courte on prend un globe 2 points quelconques A et B, un cercle de même rayon que la Terre>>> C cercle doit passer par les pts A et B et on obtient alors sur le cercle la distance la plus courte ...

Pour la distance loxodromique, lorsque ces 2 points sont sur les mêmes parallèles, on prend un cercle aussi mais de taille adaptable (on le pense bien entendu sinon ) >>La distance loxodromique passe par le parallèle qui relie ces points ! Et si ils ne sont pas sur une même parallèle, on incline le globe ou la Terre en pensée, et on fabrique un nouveau pole en se débrouillant pour que ces points soient sur la même parallèle !!
Ce qui fait que l'on a 2 cercles, un orthodromique plus petit,l' autre loxodromique plus grand qui ont une corde en commun AB ce qui donne le dessin :
La distance ortho est la distance de l' arc AB noir, et l' autre distance loxo l' arc AB rouge, et le rouge passe forcément au dessus de l' arc noir alors >>>>>>lA DISTANCE EST FORCEMENT PLUS GRANDE !>>>
C'est ça qui me pose problème, je n' arrive pas à le démontrer facilement?? .Ma question est là !
En calculant la corde AB égale aux 2 et en appelant AB' la distance rouge et AB la distance noire alpha' l'angle correspondant à l' arc rouge alpha l' angle correspondant à l' arc noir j' arrive à :
AB/AB'=alpha/alpha' x sin.alpha'/sin.alpha ! >>Je ne sais pas ou plus comment démontrer que ce rapport doit être plus grand que 1,alpha' étant plus grand que alpha
Résumé : Comment peut-on démontrer facilement que AB'(distance loxo) qui passe au dessus est forcément plus grand que AB(distance ortho) qui passe au dessous....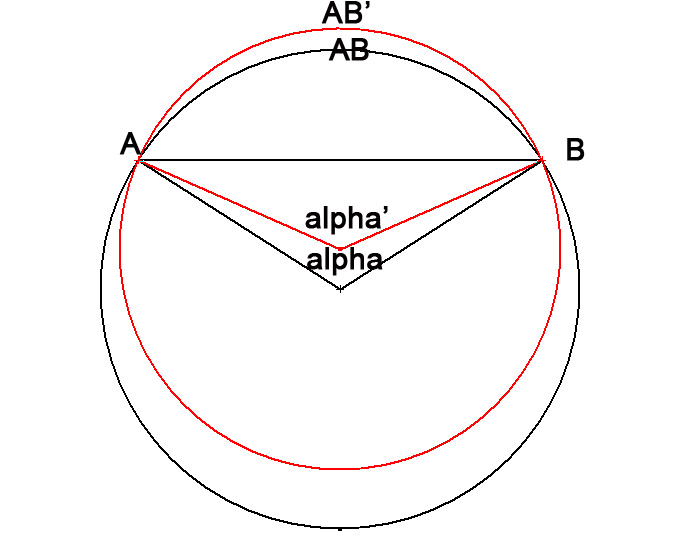
-----

[eudea-panjclinne]

L'orthodromie désigne la géodésique, le chemin le plus court, entre deux points d'une sphère. C'est donc le plus petit des deux arcs de grand cercle qui passe par ces deux points. Les grands cercles de la sphère sont obtenus par l'intersection d'un plan passant par le centre de la sphère et la sphère. Les méridiens sont des grands cercles, mais pas les parallèles sauf l'équateur.
Une loxodromie (du grec lox(o)- et -dromie course (δρόμος) oblique (λοξός)), est une courbe qui coupe les méridiens d'une sphère sous un angle constant. C'est la trajectoire suivie par un navire qui suit un cap constant.
Entre deux points A et B, l'orthodromie est inférieure ou égale à la loxodromie, par définition d'une géodésique. De plus, on montre mathématiquement que les géodésiques de la sphère sont seulement les grands cercles.
Comme la loxodromie n'est pas un grand cercle, car en s'approchant d'un pôle elle spirale autour ce qu'on constate facilement, donc une loxodromie est strictement plus grande qu'une orthodromie.

[1max2]

Oui, merci pour votre réponse mais vous ne m' avez pas lu sans sans doute, je le constate aussi , avez-vous compris le dessin que je fournis, ma question, est "Comment on démontre que l' arc AB' est plus grand que l' arc AB en dessous, ou se contente -on de dire que c'est "évident ! " ??Ou sinon comment démontrer que AB/AB'=alpha/alpha' x sin.alpha'/sin.alpha est plus petit que 1 (je crois que par erreur au dessus j' ai écrit plus grand que 1 ) >>>Preuve qu'on ne m' a pas lu j' ai fait la faute exprès (non je déconne ! )

[gg0]

Bonjour.

Je n'ai pas le temps, mais sans doute peut-on utiliser les variations de sin(x)/x, qui est décroissante et positive de 0 à pi.

Cordialement.

[A voir en vidéo sur Futura]

[eudea-panjclinne]

Pour la distance loxodromique, lorsque ces 2 points sont sur les mêmes parallèles, on prend un cercle aussi mais de taille adaptable (on le pense bien entendu sinon ) >>La distance loxodromique passe par le parallèle qui relie ces points ! Et si ils ne sont pas sur une même parallèle, on incline le globe ou la Terre en pensée, et on fabrique un nouveau pole en se débrouillant pour que ces points soient sur la même parallèle !!

Je suppose qu'il s'agit de loxodromies par rapport au méridiens. Quand les deux points sur sur un même parallèle la loxodromie est la parallèle entre ces deux points, je suis d'accord. L'angle de la loxodromie avec les méridiens est constant et égal à 90º. Où je doute c'est après, quand les deux points ne sont plus sur un même parallèle, vous effectuez une rotation de la terre qui amène un parallèle sur les deux points ce qui prouverait que toutes les loxodromies sont des cercles de la sphère ce qui est faux, ce sont des courbes non élémentaires. Loxodromie de la sphère

[1max2]

Alors là les bras m'en tombent des mains !Ne pensez-vous pas qu'en inclinant la Terre convenablement, en changeant les pôles, on peut décider que n'importe quel couple de point peut être sur le même parallèle , cela me semble évident , mais je peux me tromper !

[mach3]

En loxodromie, ne parcourt-on pas un genre de spirale plutôt qu'un cercle?

m@ch3

[mach3]

En loxodromie, ne parcourt-on pas un genre de spirale plutôt qu'un cercle?

m@ch3

oui, les sources concordent, une loxodromie (rhumb line en anglais), est une spirale commençant en un pôle et aboutissant à l'autre, en gardant un angle constant avec les méridiens. Sur une projection Mercator, c'est une droite.

m@ch3

[eudea-panjclinne]

@1max2
Si on appelle a l'angle fait la loxodromie avec le méridien, pour a=0 la loxodromie est le méridien, pour a=90º la loxodromie est le parallèle. Pour 0<a<90º c'est plus compliqué.

En loxodromie, ne parcourt-on pas un genre de spirale plutôt qu'un cercle?

Effectivement. Pour 0<a<90º c'est une courbe qui s'apparente à une spirale. On peut se convaincre de cela en faisant le dessin d'une loxodromie, a=45º, au voisinage d'un pôle. Or, une spirale n'est pas un cercle de la sphère. Voir le site référencé dans mon message #2.

[SK69202]

Il me semble que ça marche parce que le rayon équatorial n'est pas identique au rayon polaire sur la sphère terrestre.

[ansset]

Il me semble que ça marche parce que le rayon équatorial n'est pas identique au rayon polaire sur la sphère terrestre.

pas du tout !
et concernant la démo, il vaut bien mieux considérer une sphère qu'un cercle.

[1max2]

Merci pour vos réponses !Il s' agit donc d'un pb de définition pour loxodromie,je me doutais qu'il y avait d' autres courbes que le cercle, mais ce qui m'importe c'est que toutes ces courbes qui passent au dessus du cercle AB(courbe orthodromique) comme sur mon dessin de mon premier message mess1 sont plus longues.....La courbe orthodromique étant celle qui a le moins de courbure si on peut parler de courbure pour la spirale !

Ma question est : même si ça semble évident comment on démontre que toutes les courbes qui passent au dessus de AB sont plus longues que AB étant donné que toutes ces courbes ont la corde AB en commun ?

[gg0]

"sans doute peut-on utiliser les variations de sin(x)/x, qui est décroissante et positive de 0 à pi."

[1max2]

Oui, en fait on a une fonction du genre f(x)/f(x') avec f croissante et x >x' donc le rapport f(x)f(x') est plus grand que 1 quelque soit x et x' ..Ca doit être quelque chose comme ça !