/!\ TPE sur la forme de l'arc en ciel /!\

[ThoMelAnnael]

Bonjour,
Nous sommes trois élèves de première S qui travaillent pour leur TPE sur la forme de l'arc en ciel. Nous présentons notre projet dans quelques jours mais quelques questions persistent à nous poser problème et nous ne pourrions y répondre si elles nous étaient posées pendant l'oral.

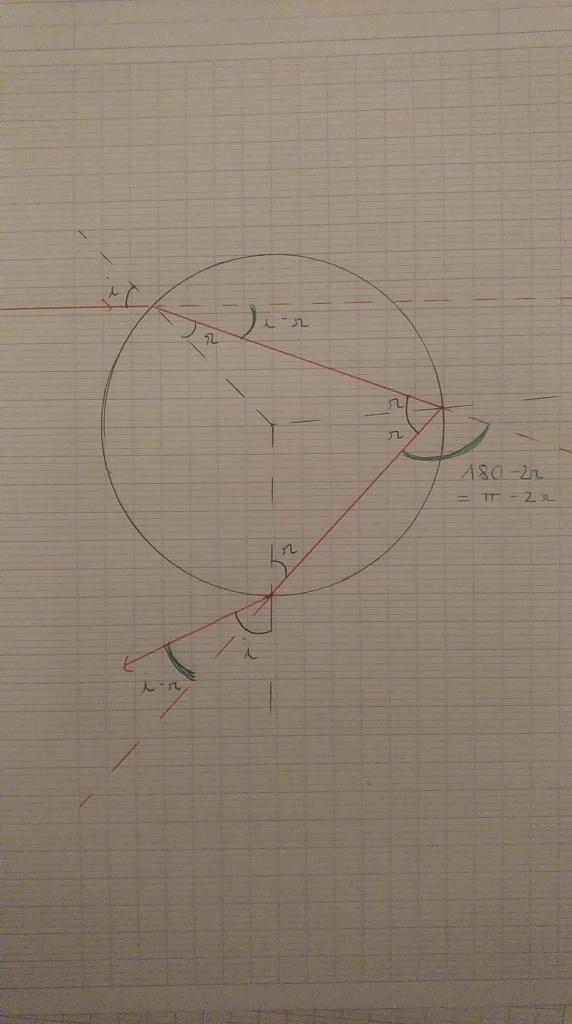
1) Pour notre TPE nous étudions le trajet de la lumière dans une goutte d'eau, ainsi vient ma question, pourquoi est ce que les angles i sont-ils égaux sur le schéma ci-dessous ?

arc 1.gif


2) Nous avons utilisé la formule de la déviation ci-dessus, mais comment la démontrer ?


3) Nous avons créé la fonction f(x)= pi – [ 2x - 4 ( sin-1 ( sin (x) / 1.33 ) ) ] définissant la déviation avec x=i afin de prouver que l'angle entre la génératrice du cône et la droite du point antisolaire était bien de 42° (voir schéma ci dessous).

arc 2.gif

Nous avons tracé la courbe de f :

arc 3.png

Puis notre prof nous a dit de nous intéresser au point A(1.04 ; 2.41), valeur minimale de f(x) sur [ 0 ; + ∞ [ qui s'est avéré, après conversion en degré, correspondre à l'angle de déviation de 42° recherché. Mais au final, pourquoi choisir la valeur minimale de déviation ?


Merci d'avance pour vos réponses !
-----

[gg0]

Bonsoir.

1) C'est quasiment dit sur le schéma : l'angle r est déterminé par i et détermine i. Ne reste plus qu'à voir pourquoi il y a égalité des 4 angles r. Pour ceux où il y a réflexion, c'est la règle de la réflexion des rayons lumineux; pour le premier et le deuxième, c'est de la géométrie du collège (tracer la médiatrice de la corde qui les joint). A vous de faire la preuve géométrique.
2) Quelle formule ? Sin(i)=sin(r) ? C'est un principe de physique dont vous pouvez trouver une démonstration sur Internet (Lois de Snell-Descartes), mais comme cette preuve s'appuie sur des principes et des calculs de niveau plus élevé, vous pourrez vous dispenser de la preuve. le nom suffira.

Cordialement.

[gg0]

3) Ça a un rapport avec le principe physique qui donne les lois de Snell-Descartes : La lumière choisit le chemin le plus court (principe de Fermat), en tout cas, parmi les chemins proches.

Reste à voir pourquoi les couleurs se séparent (le n n'est à 1,33 que pour une couleur particulière, dans les jaunes), mais c'est nettement plus compliqué (dépendance de la longueur d'onde).

Cordialement.

[jacknicklaus]

Bonsoir,

sans faire ton TPE à ta place, quelques pistes de réflexion sur tes 3 questions


1) si on suppose connus les indices de réfraction de l'eau et de l'air, si on se place au 1er point de réfraction, la donnée de l'angle i permet de trouver celle de l'angle r... Or au 3 ème point, lui aussi de réfraction, les indices de l'eau et de l'air sont toujours les mêmes, donc ...

2) la façon même dont la formule est écrite donne la réponse. tu vois qu'elle est composée de la somme de 3 termes, et (tiens quel hasard !!) , il y a trois points qui participent à la déviation... Cherche un peu...

3) cette question est plus subtile. Déjà, ton x dans ton f(x) est un angle. Penses tu utile de représenter x dans [0, infini [ ?? Ensuite, au point A, il existe toute une plage de valeurs de x pour laquelle la valeur de f(x) est à peu près identique. Essaie de matérialiser çà en prenant une marge de +- 5% par exemple pour la valeur de f(x) et vois quelle plage de valeurs de x correspond. Ensuite, demande toi ce que ca veut dire, physiquement, qu'une relativement grande plage de valeurs de x (=l’angle d'entrée "i") corresponde à à peu près la même valeur de f(x) (=la déviation finale). Fait un raisonnement purement qualitatif, et raisonne en terme de luminosité.

[A voir en vidéo sur Futura]

[ThoMelAnnael]

Premièrement, merci pour vos réponses !

1) J'ai compris, merci pour votre aide.

2) J'ai beau y réflechir je ne vois vraiment pas comment on peut arriver à cette formule, la présence du pi me laisse penser qu'il faut utiliser les notions d'angles orientés et de cercle trigonométrique mais nous venons à peine d'aborder ce chapitre donc je dois avouer être un peu larguée ..

3) gg0 : Je ne saisi pas vraiment le rapport entre ma question et la dispersion de la lumière, surtout que je crois avoir bien cerné tout ce qui concerne cette partie du tpe.

jacknicklauss : Je n'ai absolument pas comprises les notions de matérialisation de plages de valeurs et de marge que vous évoquez

[jacknicklaus]

question 2)
tu cherches des complications là où il n'y en a pas. On te donne la solution toute cuite en 3 termes : D = (i-r) + (180° - 2r) + (i-r).
Raisonne en reconstituant chaque terme à chacune des 3 étapes de déviation

premiere étape : prolonge la ligne d'arrivée (celle de l'angle incident i), et regarde l'écart avec la ligne de sortie. Quel est l'écart entre les deux, c'est à dire l'angle de déviation ?
seconde étape : idem. prolonge la ligne d'arrivée, et regarde l'angle d'écart avec la ligne de sortie
troisième étape : idem

[ThoMelAnnael]

Ah d'accord je comprends enfin, merci !

[gg0]

La dispersion de la lumière en fonction de sa longueur d'onde (couleur) est ce qui explique les couleurs de l'arc en ciel. Mais ça ne semble pas faire partie de votre travail; ce qui n'interdit pas d'y avoir pensé

Bonne continuation !